 |
Главная |
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №3
|
из
5.00
|
Задано сечение, составленное из прокатных профилей: швеллера № 16а и двух неравнобоких уголков 80´50´6 (Рисунок 8). Требуется вычислить главные центральные моменты инерции.
|


|


Рисунок 8 - Расчетная схема первого сечения
1. Из таблиц сортамента выписываются геометрические характеристики
прокатных профилей, составляющих заданное сечение.
Швеллер №16а: размеры h =160 мм, b = 68 мм, площадь сечения  ; осевые моменты инерции
; осевые моменты инерции  координата центра тяжести
координата центра тяжести  .
.
Неравнобокий уголок  : площадь сечения
: площадь сечения 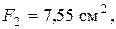 осевые моменты инерции
осевые моменты инерции  координаты центра тяжести
координаты центра тяжести  .
.
Примечание. Если в состав сечения входит прямоугольник, то для него по формулам (3.6) следует вычислить площадь и осевые моменты инерции
 (3.6)
(3.6)
В соответствии с заданным вариантом сечения выполняется чертеж в масштабе 1:2 с указанием характерных размеров.
На чертеж наносятся центры тяжести швеллера 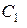 и уголка
и уголка  и проводятся их собственные центральные оси
и проводятся их собственные центральные оси  и
и  (см. Рисунок 8).
(см. Рисунок 8).
2. Определение положения центра тяжести заданного сечения.
Заданное сечение имеет одну ось симметрии, которая является главной центральной осью. Выбираем исходную систему координат: ось абсцисс y / совмещаем c нижней границей сечения, а ось ординат Z - с осью симметрии. Координаты точек 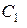 и
и  легко определяются по чертежу.
легко определяются по чертежу.
Используя формулу (3.2) и учитывая симметрию сечения, вычисляем ординату его центра тяжести по формуле
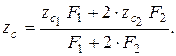
где F1 - площадь швеллера,  ,
,
 - ордината точки
- ордината точки  ,
,  ;
;
 - площадь одного уголка,
- площадь одного уголка, 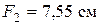 2;
2;
 - ордината точки -
- ордината точки -  ,
,  .
.
После подстановки числовых значений получаем
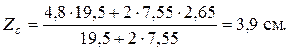
Откладывая найденное значение 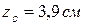 на оси Z вверх от оси y/, находим положение центра тяжести всего сечения C и проводим главные центральные оси Y , Z.
на оси Z вверх от оси y/, находим положение центра тяжести всего сечения C и проводим главные центральные оси Y , Z.
Примечание. Если фигура имеет две оси симметрии, центр тяжести лежит на их пересечении, то вычислений для определения его положения производить не нужно.
3. Вычисление главных центральных моментов инерции сечения относительно осей Y и Z .
Расстояния между осями определяются по чертежу:


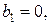 так как оси Z и
так как оси Z и  совпадают;
совпадают;

Главные центральные моменты инерции составного сечения 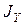 и
и  вычисляются по формулам (4.5):
вычисляются по формулам (4.5):
 (3.7)
(3.7)
После подстановки числовых значений в формулы (4.7),получаем:

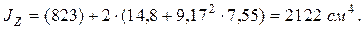
ВТОРОЙ ВАРИАНТ РЕШЕНИЯ ЗАДАЧИ №3
Задано сечение (Рисунок 9). Размеры сечения заданы в сантиметрах.
 |  | ||


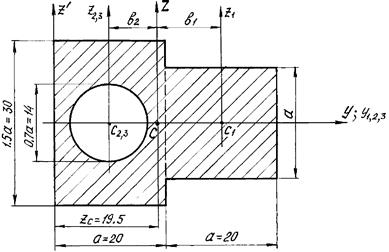
Рисунок 9 - Расчетная схема второго сечения
Требуется определить главные центральные моменты инерции этого сечения.
1. Заданное сечение вычерчивается в масштабе 1:2 и разбивается на простейшие фигуры: квадрат (1), прямоугольник (2) и круговое отверстие (3). На чертеже показываются центры тяжести составляющих фигур (точки  и
и 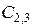 ) и проводятся их главные центральные оси
) и проводятся их главные центральные оси  ;
;  и
и  (см. Рисунок 12). Площади и моменты инерции составляющих фигур относительно их центральных осей вычисляются по известным формулам.
(см. Рисунок 12). Площади и моменты инерции составляющих фигур относительно их центральных осей вычисляются по известным формулам.
Для квадрата
 ;
;

Для прямоугольника


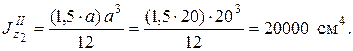
Для круга


2. Определение положения центра тяжести составного сечения.
Центр тяжести составной фигуры лежит на ее  оси симметрии Y. Вспомогательная ось z/ совмещается с левой границей сечения. Координата центра тяжести всего сечения
оси симметрии Y. Вспомогательная ось z/ совмещается с левой границей сечения. Координата центра тяжести всего сечения  в системе Yoz/ определяется по формуле (3.2):
в системе Yoz/ определяется по формуле (3.2):
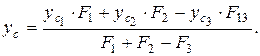
По чертежу определяются абсциссы точек  и
и  :
:


Площадь круга подставляется в формулу (3.2) со знаком минус, так как площадь отверстия принято считать отрицательной величиной.
Подставляя числовые значения, получаем

Откладывая на оси Y отрезок ОС =19,5 см, находим точку С - центр тяжести составного сечения и проводим главную центральную ось Z, параллельную оси z / (см. Рисунок12).
3. Вычисление моментов инерции относительно главных центральных осей Y, Z.
Используем формулы (3.5), как и в предыдущем примере. Перед последним слагаемым в скобках ставится знак минус, так как моменты инерции отверстия считаются отрицательными:
 (4.8)
(4.8)
Моменты инерции составляющих фигур относительно собственных главных центральных осей вычислены ранее. Оси  и
и  совпадают с главной центральной осью Y всей фигуры, поэтому расстояния между этими осями и осью Y равны нулю:
совпадают с главной центральной осью Y всей фигуры, поэтому расстояния между этими осями и осью Y равны нулю:

По чертежу находим расстояние между осями Z и 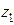
 см.
см.
и расстояние между осями Z и 
 см.
см.
Подставляя числовые значения в (3.8), вычисляем главные центральные моменты инерции составного сечения:

 .
.
ЗАДАЧА № 4
К стальному брусу круглого поперечного сечения приложены четыре крутящих момента  , три из которых известны.
, три из которых известны.
Требуется:
1) установить, при каком значении момента Х угол поворота правого концевого сечения равен нулю;
2) при найденном значении Х построить эпюру крутящих моментов;
3) при заданном значении допускаемого напряжения [t] определить диаметр вала из условия его прочности и округлить величину диаметра до ближайшей большей стандартной величины, равной 30, 35, 40, 45, 50, 60, 80, 90, 100 мм;
4) проверить, выполняется ли условие жесткости бруса при выбранном диаметре, если допускаемый угол закручивания  1 град/м;
1 град/м;
5) построить эпюру углов закручивания.
Для всех вариантов принять модуль сдвига для стали 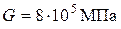
Числовые данные берутся из таблицы 4, расчетные схемы - по Рисунку 10.
Таблица 4 - Числовые данные к задаче № 4
| Номер строки | Номер расч. схемы по | Размер, м | Момент, кН× м | [t], МПа | ||||
| Рисунок 6 | а | B | с | 
| 
| 
| ||
| 0,8 | 0,4 | 1,0 | 2,0 | 1,6 | 1,0 | |||
| 0,6 | 0,5 | 0,5 | 1,8 | 1,7 | 1,2 | |||
| 0,4 | 0,7 | 0,7 | 1,7 | 0,9 | 0,7 | |||
| 0,6 | 0,4 | 0,6 | 1,5 | 0,8 | 1,5 | |||
| 0,5 | 0,8 | 0,4 | 1,3 | 2,0 | 1,4 | |||
| 0,7 | 1,0 | 0,8 | 1,0 | 1,7 | 2,0 | |||
| 1,0 | 0,7 | 1,0 | 1,6 | 1,5 | 1,6 | |||
| 0,4 | 0,6 | 0,5 | 1,4 | 1.6 | 1,8 | |||
| 0,7 | 0,4 | 0,6 | 1,5 | 0,8 | 0,9 | |||
| 0,5 | 0,5 | 0,4 | 0,9 | 1,0 | 1,5 |

Рисунок 10 - Расчетные схемы к задаче № 4
|
из
5.00
|
Обсуждение в статье: ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №3 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

