 |
Главная |
Свойства определителей
|
из
5.00
|
1°.Определитель матрицы А равен определителю транспонированной матрицы  , т. е.
, т. е.
det A = det  .
.
2°. Если хотя бы одна строка матрицы А состоит из нулей, то определитель этой матрицы равен нулю.
3°. °. Определитель матрицы, содержащей две одинаковые строки, равен нулю
4. При перестановке (транспозиции) любых двух строк в матрице, у определителя этой матрицы изменится знак.
5°. Если все элементы некоторой строки матрицы умножить на действительное число 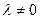 , то определитель этой матрицы умножится на
, то определитель этой матрицы умножится на  .
.
6°. Пусть матрицы А, В, С отличаются друг от друга только k-й строкой, причем элементы k-й строки матрицы С равны сумме соответствующих элементов k-х строк матриц А и В т.е.


тогда 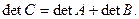
7°. Определитель матрицы не изменится, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на число  .(8°. (Теорема аннулирования). Сумма произведений элементов, какой либо строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е.
.(8°. (Теорема аннулирования). Сумма произведений элементов, какой либо строки на алгебраические дополнения соответствующих элементов другой строки равна нулю, т.е.  ) (2.7)
) (2.7)
Опр. 15.Матрица называется невырожденной, если  , и вырожденной в противном случае.
, и вырожденной в противном случае.
Определитель выгоднее раскрывать по ТОЙ строке (столбцу), где:
1) нулей побольше;
2) числа поменьше.
1.Вычислить определитель 2на 2.
2.3 на 3
1.Вычислить определитель 
2.3 Обратная матрица.
Рассмотрим квадратную матрицу  . Обратную матрицу . Обратную матрицу  можно найти по следующей формуле: можно найти по следующей формуле:
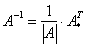 , где , где  – определитель матрицы – определитель матрицы  , ,  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Пример 1:
Найти обратную матрицу для матрицы .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.
Пример 1:
Найти обратную матрицу для матрицы 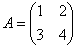 Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
 Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось,
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось,  , а значит, всё в порядке.
2) Находим матрицу миноров , а значит, всё в порядке.
2) Находим матрицу миноров  .
Матрица миноров имеет такие же размеры, как и матрица .
Матрица миноров имеет такие же размеры, как и матрица  , то есть в данном случае , то есть в данном случае  . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице . Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.
Возвращаемся к нашей матрице 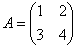  – матрица миноров соответствующих элементов матрицы – матрица миноров соответствующих элементов матрицы  .
3) Находим матрицу алгебраических дополнений .
3) Находим матрицу алгебраических дополнений 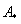 .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел: .
Это просто. В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:   – матрица алгебраических дополнений соответствующих элементов матрицы – матрица алгебраических дополнений соответствующих элементов матрицы  .
4) Находим транспонированную матрицу алгебраических дополнений .
4) Находим транспонированную матрицу алгебраических дополнений  . .
 – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы  .
5) Ответ. Вспоминаем нашу формулу .
5) Ответ. Вспоминаем нашу формулу 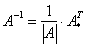 Таким образом, обратная матрица:
Таким образом, обратная матрица: 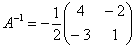 Как проверить решение?
Необходимо выполнить матричное умножение
Как проверить решение?
Необходимо выполнить матричное умножение  либо либо 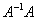 Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие
Получена так называемая единичная матрица (с единицами по главной диагонали и нулями в остальных местах).
Таким образом, обратная матрица найдена правильно.
Если провести действие 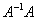 , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно. , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно.
|
2.4. Ранг матрицы
Рассмотрим прямоугольную матрицу  . Выберем в матрице А произвольно k строк сномерами i1, i2, … , ik и k столбцов с номерами j1, j2, ... , jk, . Выберем в матрице А произвольно k строк сномерами i1, i2, … , ik и k столбцов с номерами j1, j2, ... , jk,  . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Как мы уже знаем, определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу Аk порядка k.
Как мы уже знаем, определитель матрицы Аk называется минором k-гo порядка (минором порядка k) и обозначается  или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если или, когда не важно, какие именно строки и столбцы выбраны, обозначается Mk, т.е. по определению Mk = det Аk. Например, если
 и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
и выбраны строки c номерами i1 = 1, i2 = 3 и столбцы с номерами j1 = 2, j2 = 4, то
 Число миноров второго порядка для этой матрицы равно 18.
Опр.16.Наивысший порядок миноров, не равных нулю, называется рангомматрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
Число миноров второго порядка для этой матрицы равно 18.
Опр.16.Наивысший порядок миноров, не равных нулю, называется рангомматрицы и обозначается символами: rаng А или rA.
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r.
Пример 1.2. Найти ранг матрицы:
 .
Решение. Здесь .
Решение. Здесь 
 ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число ,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:
1) перестановка (транспозиция) строк (столбцов) матрицы;
2) умножение всех элементов отроки (столбца) матрицы на действительное число 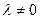 ;
3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.
Утверждение 2.2. Элементарные преобразования не изменяют ранга матрицы. ;
3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число.
Утверждение 2.2. Элементарные преобразования не изменяют ранга матрицы.
|
|
из
5.00
|
Обсуждение в статье: Свойства определителей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

