П.6.7. Поверхности второго порядка

Пусть в пространстве задана прямоугольная декартова система координат 0xyz. Поверхность называется поверхностью второго порядка, если она задается уравнением второй степени относительно текущих координат х, у, z.

1.Сферой называется множество точек в пространстве, удаленных от данной точки (называемой центром) на одно и то же расстояние (называемое радиусом).

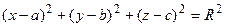
– уравнение сферы с центром в точке S(a, b, c) и радиусом R. Если центр совпадает с началом координат 0(0, 0, 0), то получаем

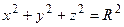
– каноническое уравнение сферы.

Эллипсоиды.

Эллипсоидом называется поверхность, задаваемая в декартовой системе координат уравнением

Числа а, b, с называются полуосями эллипсоида.

Рис.1. Эллипсоид.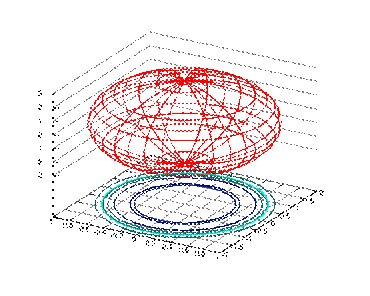

Цилиндрические поверхности.

Цилиндрической поверхностью называется множество всех прямых, пересекающих данную линию L и параллельных данной прямой l. Линия L называется направляющей для цилиндрической поверхности, а прямые, составляющие ее (параллельные прямой l), называются ее образующими .

Итак, данная цилиндрическая поверхность в пространстве задается уравнением: F(x, у) = 0 (как и ее направляющая L в плоскости 0ху).

В пространстве 0xyz линия L будет задаваться системой уравнений:

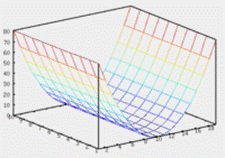
Нас интересуют цилиндрические поверхности второго порядка, следовательно,их направляющими будут: окружность, эллипс, гипербола, парабола. Сами поверхности будут называться соответственно: круговым цилиндром, эллиптическим цилиндром, гиперболическим цилиндром и параболическим цилиндром.

Эллиптический цилиндр:	Параболический цилиндр:	Гиперболический цилиндр:
Рис.2. Циллиндрические поверхности.

Конические поверхности.

Коническая поверхность — поверхность с вершиной и направляющей , содержащая все точки всех прямых, проходящих через точку и пересекающихся с кривой .

Каноническое уравнение круговой конической поверхности в декартовых координатах .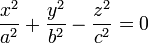

Рис.3. Коническая поверхность.

Гиперболоиды.

Однополостным гиперболоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением

Двуполостным гиперболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:

:	Однополостной гиперболоид:	Двуполостной гиперболоид

Рис.4. Гиперболоиды.

Параболоиды.

Эллиптическим параболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:

,

где р и q одного знака.

Рис.5. Параболоид эллиптический.

Гиперболическим параболоидом называется поверхность, уравнение которой имеет вид:

где р и q одинакового знака.

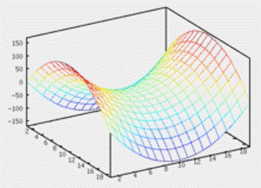
Рис.6. Параболоид гиперболический.