 |
Главная |
Если «икс» стремится к «минус бесконечности»
|
из
5.00
|
Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых 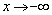 . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
. Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел 
Значение предела зависит только от слагаемого  , поскольку оно обладает самым высоким порядком роста. Если
, поскольку оно обладает самым высоким порядком роста. Если 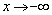 , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени, в данном случае – в четвёртой, равно «плюс бесконечности»:
, то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени, в данном случае – в четвёртой, равно «плюс бесконечности»: 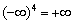 . Константа («двойка») положительна, поэтому:
. Константа («двойка») положительна, поэтому:

2) Вычислим предел 
Здесь старшая степень опять чётная, поэтому:  . Но перед
. Но перед  расположился «минус» (отрицательная константа –1), следовательно:
расположился «минус» (отрицательная константа –1), следовательно:

3) Вычислим предел 
Значение предела зависит только от 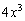 . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае:
. Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае:  .
.
Константа («четвёрка») положительна, значит:

4) Вычислим предел 
Первый парень на деревне  снова обладает нечётной степенью, кроме того, за пазухойотрицательная константа, а значит:
снова обладает нечётной степенью, кроме того, за пазухойотрицательная константа, а значит:  Таким образом:
Таким образом:
 .
.
Пример 5
Найти предел 
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость  . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
. Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:

Решение тривиально:

Разделим числитель и знаменатель на 

Пример 6
Найти предел 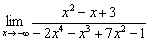
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел 
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость  . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
. Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:

Решаем:

Разделим числитель и знаменатель на 

Почему  ?
?
Проанализируем бесконечно малые слагаемые знаменателя:
Если 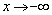 , то слагаемые с чётными степенями
, то слагаемые с чётными степенями  будут стремиться к бесконечно малым положительным числам (обозначаются через
будут стремиться к бесконечно малым положительным числам (обозначаются через 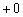 ), а слагаемые с нечётнымистепенями
), а слагаемые с нечётнымистепенями 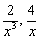 будут стремиться к бесконечно малым отрицательным числам (обозначаются через
будут стремиться к бесконечно малым отрицательным числам (обозначаются через 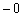 ).
).
Теперь зададимся вопросом, какое из этих четырёх слагаемых  будет стремиться к нулю (неважно с каким знаком) медленнее всего? Вспомним наивный приём: сначала «икс» равно –10, потом –100, затем –1000 и т.д. Медленнее всего к нулю будет приближаться слагаемое
будет стремиться к нулю (неважно с каким знаком) медленнее всего? Вспомним наивный приём: сначала «икс» равно –10, потом –100, затем –1000 и т.д. Медленнее всего к нулю будет приближаться слагаемое  . Образно говоря, это самый «жирный» ноль, который «поглощает» все остальные нули. По этой причине на завершающем этапе и появилась запись
. Образно говоря, это самый «жирный» ноль, который «поглощает» все остальные нули. По этой причине на завершающем этапе и появилась запись  .
.
Следует отметить, что знаки бесконечно малых слагаемых числителя нас не интересуют, поскольку там нарисовалась осязаемая добротная единичка. Поэтому в числителе я поставил «просто нули». К слову, знаки при нулях не имеют значения и во всех примерах, где в пределе получается конечное число (Примеры №№5,6).
Без измен, на то он и математический анализ, чтобы анализировать =)
Впрочем, о бесконечно малых функцияхпозже, а то вы нажмёте маленький крестик справа вверху =)
Пример 8
Найти предел 
Это пример для самостоятельного решения.
Рекомендую хорошо осмыслить информацию первой части урока, и по возможности сделать перерыв.
|
из
5.00
|
Обсуждение в статье: Если «икс» стремится к «минус бесконечности» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

