Повторим: «Элементарные преобразования не изменяют решение системы»

2015-11-09

1086

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

ВНИМАНИЕ!:рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицамичто-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе . Она уже почти решена.

Что просит Гаусс? Он говорит: «Запишите расширенную матрицу системы и с помощью элементарных преобразований приведите ее к ступенчатому виду».

В данном случае для этого

(1) Ко второй строке прибавьте первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Разделите вторую строку на 3. Почему? Чтобы вторая строка давала сразу значение второй переменной.

Цель элементарных преобразований–привести матрицу к ступенчатому виду:

.

В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.

В результате элементарных преобразований получена система уравнений, эквивалентная исходной системе линейных уравнений, которая приняла вид:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

В нижнем уравнении у нас уже готовый результат: . Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:

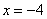
Ответ:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Пример 1

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас мы сразу нарисуем результат, к которому мы придём в ходе решения:

Повторимся, что наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица. Вообще говоря, устроит и (–1), а иногда и другие числа, но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения. Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18).

И последовательно проводим (опять же мысленно или на черновике) сложение, т. е. ко второй строке прибавляем первую строку, уже умноженную на –2:

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3.

Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

Результат записываем в третью строку:

.

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО:

.

А мысленный ход самих расчётов мы уже рассмотрели выше.

Далее нужно получить единицу на следующей «ступеньке»:

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

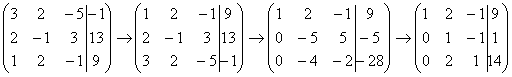
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2:

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на (–2) и проведите сложение. Последнее выполненное действие – причёска результата, для этого делим третью строку на 3.

В результате элементарных преобразований получена система, эквивалентная исходной системе линейных уравнений:

Теперь в действие вступает «обратный ход» метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение: 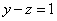. Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение: 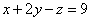. «Игрек» и «зет» известны, дело за малым: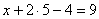

Ответ:

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Пример 2

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!

Пример 3

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами.

Поступим так:

(1) К первой строке прибавляем вторую строку, умноженную на (–1). То есть, мысленно умножили вторую строку на (–1) и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху (–1), что нас вполне устроит. Кто хочет получить (+1), может выполнить дополнительное телодвижение: умножить первую строку на (–1), сменив у неё знак. Дальше алгоритм работает уже по накатанной колее:

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на (–1). В принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:

Ответ: .

Пример 4

Решить систему линейных уравнений методом Гаусса

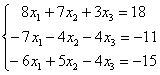
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваш ход решения может отличаться от нашего хода решения.

2015-11-09

1086

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 10 11 12 13 141516 17 18 19 Следующая ⇒

Обсуждение в статье: Повторим: «Элементарные преобразования не изменяют решение системы»

Обсуждений еще не было, будьте первым... ↓↓↓