Понятие комплексного числа

«Комплексное число» - это не число в обычном понимании, характеризующееся одним параметром, а математический объект, составленный из двух элементов, каждый из которых - действительное число. Если хотите, комплексное число – двумерное число.

Геометрически комплексное число может быть представлено, как точка на плоскости (элемент плоскости), на которой задана прямоугольная система координат: две взаимно перпендикулярные числовые оси (0X и 0Y) с общей нулевой точкой (0) начала отсчёта. Произвольная точка такой координатной плоскости определяется упорядоченной парой чисел (x; y), где x и y называют обычно координатами точки по соответствующим осям. Пара называется упорядоченной, т. к. при перестановке чисел x≠y местами в скобках получается другое комплексное число (другая пара): (x; y) ¹ (y; x).

Определение: Всякое комплексное число представимо в виде упорядоченной пары действительных чисел: z =(x; y), где и x, и y – действительные числа, а z – «название» этой пары. Первое в паре число x = Re(z) называют действительной частью, а второе в паре число y = Im(z) – мнимой частью комплексного числа.

Определение: Алгебраическим представлением комплексного числа z называют «число» вида: z = a + b∙i. где a и b – действительные числа, а i - мнимая единица.

Действительные числа после этого определения стали обозначать, как x º (x; 0), и отмечать их на числовой оси 0X, а мнимые числа (мнимые части комплексных чисел) – как y º (0; y). Для комплексных чисел ввели особые алгебраические операции, и оказалось, что они представимы как в виде векторов, так и «алгебраически». Например, как: z = x + i∙y, если пару (комплексную величину) i º (0; 1) назвать мнимой единицей.

Здесь действительное число a = Re(z) – действительная (реальная, real) часть z, а действительное число b = Im(z) - это мнимая (воображаемая, imagine) часть z.

А вот произведение числа b на упорядоченную пару (0; 1): b∙i = b∙(0; 1) = (0; b) является чисто мнимым числом.

Здесь a + b∙i – это обозначение единого комплексного числа, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: или переставить мнимую единицу: 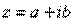– от этого комплексное число не изменится.

Но стандартно в большинстве случаев комплексное число принято записывать именно в таком порядке: z = a + b∙i.

Чтобы всё было понятнее, приведём геометрическую интерпретацию. Комплексные числа изображаются в виде двумерных точек на комплексной плоскости:

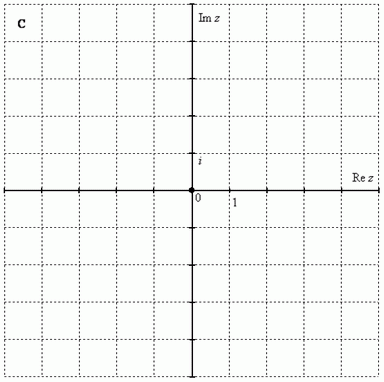Как упоминалось выше, буквой R принято обозначать множество действительных чисел. Множествоже комплексных чиселпринято обозначать «жирной» или утолщенной буквой C. Поэтому на чертеже следует поставить букву C, обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость задаётся двумя осями:

X = Re(z) - действительная ось; Y = Im(z) – мнимая ось.

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать размерность (масштаб оси). Поэтому отмечаем точки:

ноль (0; 0)

единицу 1 по действительной оси (1; 0);

мнимую единицу i по мнимой оси (0; 1).

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .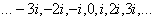

Построим на комплексной плоскости следующие комплексные числа:

, ,

, ,

, , ,

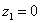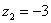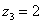
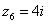
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.

Рассмотрим следующие комплексные числа: 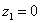, , 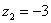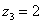. Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось Re(z) обозначает в точности множество действительных чисел R, то есть на осиRe(z) сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел R является подмножеством множества комплексных чисел C.

Числа 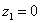, , 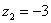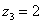– это комплексные числа с нулевой мнимой частью.

Числа , , 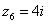– это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси Im(z).

В числах , , , и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, так как что они сливаются с осями.