 |
Главная |
Вычисление поверхностного интеграла II рода
|
из
5.00
|
Пусть гладкая поверхность S задана уравнением z = z (x,y) . Определена в замкнутой области G – проекции S на плоскость ОХУ . Рассмотрим на поверхности S
R(x,y,z) – непрерывная функция .
Разобьём S произвольно на n частей G1 , G2 , . . . ,Gn .
Выберем по произвольной точке Мi (xi , hi, Vi) .
Составим интегральную сумму :
 =
=  ,
,
где DSi – площадь Gi , так как точка Vi = Z(xi , hi) .
Переходя в (4.1) к пределу при d®0 получаем
 .
.
Аналогично :
. 
G1 – проекция S на Oyz .

G2 – проекция S на Ozх .
Связь между поверхностными интегралами I и II рода
Пусть гладкая ориентированая поверхность , на которой задана непрерывная вектор – функция  (М) = [ P(x,y,z), Q(x,y,z) , R(x,y,z)] ,
(М) = [ P(x,y,z), Q(x,y,z) , R(x,y,z)] ,  (M) – единичная нормаль = ( cosa , cosb , cosg ) , тогда
(M) – единичная нормаль = ( cosa , cosb , cosg ) , тогда

Отсюда видно , что если выбрать другую сторону поверхности , то направляющий косинус изменит знак .
Пример 6.8.11.Вычислить
 , где S - поверхность треугольника , образованного пересечением плоскости х – у +z = 1 с координатными плоскостями : х = 0 , у = 0 , z = 0
, где S - поверхность треугольника , образованного пересечением плоскости х – у +z = 1 с координатными плоскостями : х = 0 , у = 0 , z = 0  в верхней стороне поверхности .
в верхней стороне поверхности .





 .
.
Формула Остроградского
Связь между поверхностным интегралом и тройным интегралом
ТеоремаЕсли функции P(x,y,z) , Q(x,y,z) , R(x,y,z)непрерывны вместе со своими частными производными I-го порядка в области V , ограниченной замкнутой поверхностью S , то имеет место формула
 .
.
Пример 6.8.12.
 ,
,
где S – внешняя сторна сферы x2 + y2 + z2 = R2 .
Решение.
Применим формулу Остроградского :

Вводим сферические координаты
 .
.
Связь поверхностного интеграла с криволинейным интегралом. Теорема Стокса
Теорема Если Р(x,y,z) , Q(x,y,z) , R(x,y,z) есть непрерывные функции вместе со своими частными производными первого порядка на поверхности S, то имеет место формула
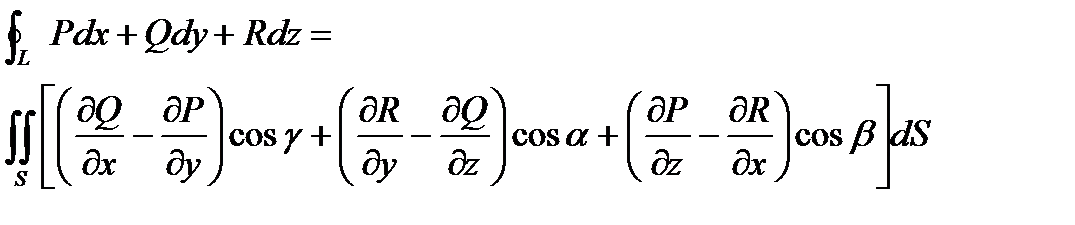 ,
,
где L – граница поверхности S ;cosa , cosb , cosg - направляющие косинусы нормали к поверхности S .
Пример 6.8.13.Вычислить с помощью формулы Стокса  ,
,
L- окружность 
А поверхностью S служит верхняя сторона полусферы x2 + y2 +z2 =1.



 .
.

Контрольные работы
Контрольная работа №1
Задание 1. Для матрицы третьего порядка вычислите ее определитель
и определитель матрицы, транспонированной к данной.
1. 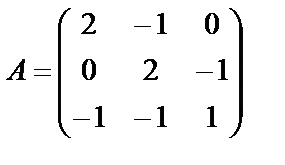 ; 2.
; 2.  ; 3.
; 3.  ;
;
4.  ; 5.
; 5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  ; 12.
; 12.  ;
;
13. 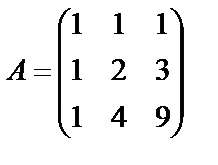 ; 14.
; 14.  ; 15.
; 15.  ;
;
16. 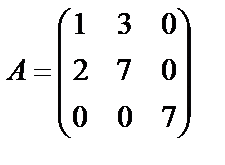 ; 17.
; 17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 
Задание 2. Вычислите определитель четвертого порядка
1.  ; 2.
; 2.  ; 3.
; 3.  ;
;
4.  ; 5.
; 5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8. 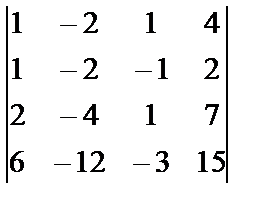 ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ; 15.
; 15.  ;
;
16.  ; 17.
; 17.  ;
;
18.  ;
;
19.  ; 20.
; 20. 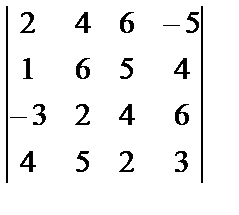
Задание 3. Найдите матрицу, обратную матрице. Проверьте результат, вычислив произведение взаимно обратных матриц.
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 
Задание 4. Решите систему линейных уравнений матричным способом.
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 
Задание 5. Решите систему линейных уравнений по формулам
Крамера.
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8 .
; 8 .  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 
Задание 6. Найдите все решения однородной системы линейных уравнений методом Гаусса.
1.  ; 2.
; 2.  ;
;
3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ;
;
7.  ; 8.
; 8.  ;
;
9.  ; 10.
; 10.  ;
;
11.  ; 12.
; 12.  ;
;
13.  ; 14.
; 14.  ;
;
15.  ; 16
; 16  ;
;
17.  ; 18.
; 18.  ;
;
19.  ; 20.
; 20. 
Задание 7. Даны координаты векторов а1, а2, а3, а4 и b в некотором базисе. Покажите, что векторы а1, а2, а3, а4 образуют базис и найдите координаты вектора b в этом базисе.
1. а1(1,2,-1,-2); а2(2,3,0,1); а3(1,2,1,3); а4(1,3,-1,0);b(7,14,-1,2).
2. а1(2,1,0,-1); а2(2,3,0,-2); а3(2,4,2,1); а4(0,-3,0,2);b(5,2,1,0).
3. а1(1,1,4,2); а2(2,-1,3,1); а3(0,2,0,0); а4(1,-1,0,1);b(5,0,0,5).
4. а1(1,2,3,4); а2(2,3,4,1); а3(3,4,1,2); а4(4,1,2,3);b(2,2,2,4).
5. а1(2,0,0,0); а2(0,4,0,0); а3(0,0,6,0); а4(0,0,0,8);b(6,7,0,1).
6. а1(1,2,-1,-2); а2(2,3,0,1); а3(1,2,1,3); а4(1,3,-1,0);b(6,7,0,1).
7. а1(2,3,4,5); а2(3,4,5,2); а3(4,5,2,3); а4(5,2,3,4);b(-1,2,1,-2).
8. а1(3,5,-1,-1); а2(3,5,1,4); а3(2,5,0,3); а4(1,3,-1,0);b(7,14,-1,2).
9. а1(4,4,0,-3); а2(4,7,2,-1); а3(2,1,2,3); а4(0,-3,0,2);b(5,2,1,0).
10. а1(3,0,7,3); а2(2,1,3,1); а3(1,1,0,1); а4(1,-1,0,1);b(5,0,0,5).
11. а1(3,5,7,5); а2(5,7,5,3); а3(7,5,3,5); а4(4,1,2,3);b(2,2,2,4).
12. а1(2,4,0,0); а2(0,4,6,0); а3(0,0,6,8); а4(0,0,0,8);b(-14,6,0,1).
13. а1(1,2,-1,-2); а2(3,5,-1,-1); а3(3,5,1,4); а4(2,5,0,3);b(6,7,0,1).
14. а1(2,1,0,-1); а2(4,4,0,-3); а3(2,7,2,-1); а4(2,1,2,3);b(-3,2,5,0).
15. а1(5,7,9,7); а2(7,9,7,5); а3(9,7,5,7); а4(5,2,3,4);b(-1,2,1,-2).
16. а1(1,3,5,3); а2(3,5,3,2); а3(5,3,1,3); а4(3,0,1,2);b(-6,0,2,-3).
17. а1(-1,1,3,1); а2(1,3,1,-1); а3(3,-1,-1,1); а4(2,-1,0,1);b(-3,6,7,-2).
18. а1(0,1,2,3); а2(1,2,3,0); а3(2,3,0,1); а4(3,0,1,2);b(-6,0,2,-3).
19. а1(-1,0,1,2); а2(0,1,2,-1); а3(1,2,-1,0); а4(2,-1,0,1);b(-3,6,7,-2).
20. а1(4,4,3,0); а2(-17,24,1,1); а3(-6,-1,2,0); а4(-5,3,1,0);b(-9,10,1,1).
Задание 8
По координатам вершин пирамиды а1 а2 а3 а4 найти:
1) длины ребер а1 а2 и а1 а3;
2) угол между ребрами а1 а2 и а1 аз;
3) площадь грани а1 а2 а3;
4) объем пирамиды а1 а2 а3 а4;
5) уравнения прямых а1 а2 иа1 а3;
6) уравнения плоской а1 а2 а3 иа1 а2 а4 ;
7) угол между плоскостями а1 а2 а3 иа1 а2 а4;
8) угол между ребром а1 а3 и гранью а1 а2 а4 ;
9) уравнение высоты, опущенной из вершины а4 на грань а1 а2 а3 ;
10) уравнение плоскости, проходящей через высоту пирамиды, опущенную из вершины а4 на грань а1 а2 а3 , и вершину а1 пирамиды ;
11) расстояние от вершины.а3до плоскости а1 а2 а4.
| а1 | а2 | а3 | а4 | |
| (3;1;4) | (-1;6;1) | (-1;1;6) | (0;4;-1) | |
| (3;3;9) | (6;9;1) | (1;7;3) | (8;5;8) | |
| (3;5;4) | (5;8;3) | (1;9;9) | (6;4;8) | |
| (2;4;3) | (7;6;3) | (4;9;3) | (3;6;7) | |
| (9;5;5) | (-3;7;1) | (5;7;8) | (6;9;2) | |
| (0;7;1) | (4;1;5) | (4;6;3) | (3;9;8) | |
| (5;5;4) | (3;8;4) | (3;5;10) | (5;8;2) | |
| (6;1;1) | (4;6;6) | (4;2;0) | (1;2;6) | |
| (7;5;3) | (9;4;4) | (4;5;7) | (7;9;6) | |
| (6;6;2) | (5;4;7) | (2;4;7) | (7;3;0) | |
| (0;3;2) | (-1;3;6) | (-2;4;2) | (0;5;4) | |
| (-1;2;0) | (-2;2;4) | (-3;3;0) | (-1;4;2) | |
| (2;2;3) | (1;2;7) | (0;3;3) | (2;4;5) | |
| (0;-1;2) | (-1;-1;6) | (-2;0;2) | (0;1;4) | |
| (3;0;2) | (2;0;6) | (1;1;2) | (3;2;4) | |
| (0;2;-1) | (-1;2;3) | (-2;3;-1) | (0;4;1) | |
| (2;3;2) | (1;3;6) | (0;4;2) | (2;5;4) | |
| (-1;0;2) | (-2;0;6) | (-3;1;2) | (-1;2;4) | |
| (2;0;3) | (1;0;7) | (0;1;3) | (2;2;5) | |
| (2;-1;2) | (1;-1;6) | (0;0;2) | (2;1;4) |
Задание 9
Составить общее уравнение плоскости, проходящей через точку М перпендикулярно плоскостям a и b:
| M | a | b | |
| (2;1;-5) | 3X-2Y+Z+7=0 | 5X-4Y+3Z+1=0 | |
| (1;-1;1) | X-Y+Z-1=0 | 2X+Y+Z+1=0 | |
| (2;-1;1) | 3X+2Y-Z+4=0 | X+Y+Z-3=0 | |
| (1;8;2) | 5X+6Y+11Z-3=0 | 3X+Y+4Z-12=0 | |
| (-1;-2;0) | 4X+6Y-5Z-14=0 | X+3Y-2Z-1 =0 | |
| (5;1;2) | X-7Y-2Z-10=0 | 2X-2Y-Z-13=0 | |
| (2;4;1) | X-2Y+5Z-7=0 | 2X-3Y+7Z-5=0 | |
| (1;1;1) | X-2Y+2Z+8=0 | 3X+5Y+7Z-1=0 | |
| (1;4;5) | X+Y+5Z+3=0 | 3X+2Y+8Z-9=0 | |
| (3;0;7) | X+Y+4Z=0 | 3X+2Y+7Z-2=0 |
Составить уравнение плоскости, проходящей через точки М1, М2 перпендикулярно плоскости a :
| М1 | М2 | a | |
| (2;-1;4) | (3;2;1) | X+Y+Z-3=0 | |
| (1;1;1) | (2;2;2) | X-Y-Z=0 | |
| (0;-5;0) | (0;0;2) | X+5Y+2Z-10=0 | |
| (2;0;-1) | (1;-1;3) | 3X+2Y-Z+3=0 | |
| (-1;-2;0) | (1;1;2) | X+2Y+2Z-4=0 | |
| (1;-2;4) | (2;-3;5) | X+Y-3Z+8=0 | |
| (0;1;3) | (1;2;7) | X+2Y+5Z+6=0 | |
| (1;1;0) | (2;-1;-1) | 5X+2Y+3Z-7=0 | |
| (1;4;0) | (2;14;3) | X+6Y+Z-3=0 | |
| (9;1;1) | (19;2;2) | 17X+2Y+Z+11=0 | |
| (7;1;0) | (26;2;3) | 9X+Y+Z-17=0 | |
| (0;1;2) | (-1;2;3) | X+Y-Z+2=0 | |
| (3;4;6) | (5;1;5) | X+2Y+3Z-6=0 | |
| (4;1;0) | (2;-1;1) | X-Y+Z-3=0 | |
| (1;0;1) | (-1;1;0) | X+2Y-Z-1=0 |
Задание 10
Составить канонические уравнения прямой, заданной как линия пересечения двух плоскостей a и b:
| a | b | |
| x-2у+2z-8=0 | x+2z-6=0 | |
| 3x-5y+z-8=0 | 2x+y-z+2=0 | |
| x-2y+3z-4=0 | 3x+2y-5z-4=0 | |
| x+z-6=0 | x+6y-4=0 | |
| x+2y-4=0 | x-2y+2z-8=0 | |
| x+2Z-6=0 | x+y+z-6=0 | |
| x+2y+3z-13=0 | 3x+y+4z-14=0 | |
| x+2y+3z-1=0 | 2x-3y+2z-9=0 | |
| 2x+7y-z-8=0 | Х+2y+z-4=0 |
Составить канонические уравнения прямой, проходящей через точку А параллельно прямой ℓ:
| А | ℓ | |
| (3;1;-1) | X+5y+2=0 3х+4y+2z-8=0 | |
| (2;0;-3) | 
| |
| (-4;3;0) | x-2y+z-4=0 2x+y-z=0 | |
| (2;-5;9) | 2x-3y-3z-9=0 x-2y+3=0 |
Составить канонические уравнения прямой, проходящей через точку А перпендикулярно прямым ℓ1 и ℓ2:
| А | ℓ1 | ℓ2 | |
| (2;-3;4) | 
| 
| |
| (0;1;1) | 
| 
| |
| (2;-3;4) | x=t;y=t;z=2t+5 | x=3t+8;y=2t-4;z=t+2 | |
| (0;1;-1) | x=3t+1;y=15t;z=7t-2 | x=t;y=2t-5;z=6 | |
| (0;-1;1) | x=2t;y=t-5;z=3t-2 | x=4t-1;y=4t+6;z=t-4 |
Составить канонические уравнения прямой, проходящей через точки а1 и а2:
| а1 | а2 | |
| (1;-2;1) | (3;1;1) | |
| (1;-2;1) | (0;6;5) | |
| (3;1;2) | (0;2;5) | |
| (0;1;2) | (5;2;1) | |
| (1;7;3) | (0;2;1) | |
| (1;0;2) | (5;1;4) | |
| (3;5;1) | (2;3;1) |
Задание 11
Найти проекцию точки А на плоскости a:
| А | a | |
| (1;3;1) | x+2y+2z-30=0 | |
| (3;1;-1) | 3x+y+z-20=0 | |
| (5;2;-1) | 2x-y+3z+23=0 | |
| (4;-3;1) | x-2y-z-15=0 | |
| (1;-1;0) | 5x-6y+2z-76=0 |
Найти точку, симметричную точке А относительно плоскости а:
| А | а | |
| (0;0;0;) | х-2у+4z-21=0 | |
| (1;5;2) | 2х-у-z+11=0 | |
| (1;-3;-4) | Зх-у-2z=0 | |
| (5;2;-1) | 2х-у+3z+23=0 | |
| (3;-4;-6) | 9х-7у-31z-108=0 |
Найти точку, симметричную точке А относительно прямой ℓ:
| А | ℓ | |
| (2;1;0) | 
| |
| (4;3;10) | 
| |
| (1;-1;2) | 
| |
| (3;2;0) | 
| |
| (2;-1;5) | 
| |
| (0;0;0;) | 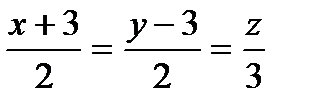
|
Составить уравнения прямой, проходящей через точки пересечения плоскостиа с прямыми ℓ1 и ℓ2:
| А | ℓ1 | ℓ2 | |
| 2x+y-3z=0 | 
| 
| |
| 3x-2y+z=0 | 
| 
| |
| 6x+3y-41=0 | 
| 
| |
| 3x-y-2z+5=0 | 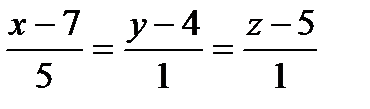
| 
| |
| 2x+3y+z-1=0 | 
| 
|
Составить уравнения прямой, лежащей в плоскости aи проходящей через точку пересечения плоскости a с прямой ℓ, перпендикулярно вектору `а:
| a | ℓ | _` а | |
| 6x+3y-z-41=0 | 
| {1;2;1} | |
| x+2y=0 | 
| {3;-1;2} | |
| x+2y=0 | 
| {5;-1;2} | |
| 3x-y-2z+5=0 | 
| {0;3;5} |
Задание 12
Составить общее уравнение плоскости, проходящей через параллельные прямые ℓ1 и ℓ2:
| ℓ1 | ℓ2 | |

| 
| |

| 
| |
| x=2t+1;y=-t;z=t+1 | 
| |

| 
| |

| 
|
Составить общее уравнение плоскости, проходящей через прямую ℓ1, параллельно прямой ℓ2:
| ℓ1 | ℓ2 | |

| 
| |

| 
| |

| 
| |

| 
| |
| x=3t-1;y=-2t-3;z=-t+2 | x=2t+2;y=3t-1;z=-5t+1 |
Составить общее уравнение плоскости, проходящей через точку М параллельно прямымℓ1 и ℓ2:
| ℓ1 | ℓ2 | М | |

| 
| (-2;0;0) | |

| 
| (6;1;1) | |

| 
| (1;2;1) | |

| 
| (1;2;3) | |

| 
| (0;0;2) |
Составить общее уравнение плоскости, проходящей через пересекающиеся прямые ℓ1 и ℓ2:
| ℓ1 | ℓ2 | |

| 
| |
| x=z-2;y=2z+1 | 
| |

| x=t+5;y=-4t-1;z=t-4 | |
| x=t+1;y=-2;z=-t+1 | x=2t;y=2t-2;z=-3t+2 | |

| x=3t+7;y=2t+2;z=-2t+1 | |

| 
| |
| x=2t-3;y=3t-2;z=-4t+6 | x=t+5;y=-4t-1;z=t-4 | |

| 
| |
| x=2t+1;y=3t-2;z=-6t+1 | 
| |

| 
|
Контрольная работа №2
ЗАДАНИЕ 1
Вычислите пределы:
1 
| 11 
| ||
2 
| 12 
| ||
3 
| 13 
| ||
4 
| 14 
| ||
5 
| |||
6 
| |||
7 
| |||
8 
| |||
9 
| |||
10 
| |||
15 
| |||
16 
| |||
17  18
18 
| |||
19 
| |||
20 
| |||
ЗАДАНИЕ 2
Вычислите пределы:
1 
| 11 
| |
2 
| 12 
| |
3 
| 13 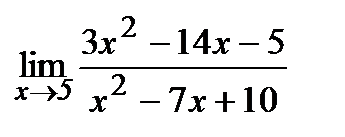
| |
4 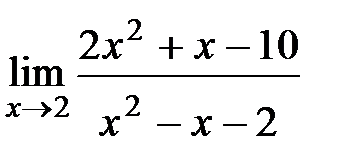
| 14 
| |
5 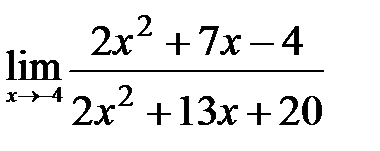
| 15 
| |
6 
| 16 
| |
7 
| 17 
| |
8 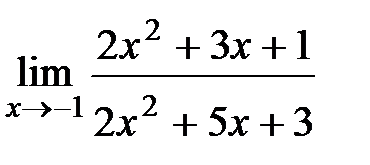
| 18 
| |
9 
| 19 
| |
10 
| 20 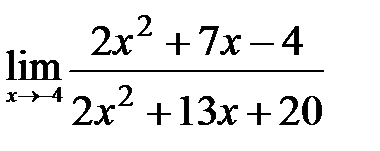
| |
ЗАДАНИЕ 3
Вычислите пределы:
а)
1 
| 11 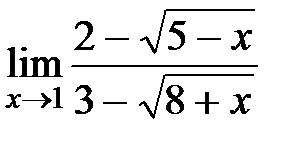
| |
2 
| 12 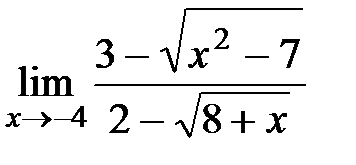
| |
3 
| 13 
| |
4 
| 14 
| |
5 
| 15 
| |
6 
| 16 
| |
7 
| 17 
| |
8 
| 18 
| |
9 
| 19 
| |
10 
| 20 
|
б)
1 
| 11 
|
2 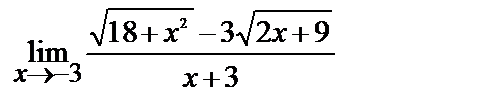
| 12 
|
3 
| 13 
|
4 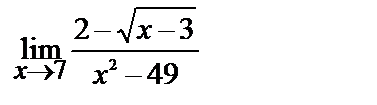
| 14 
|
5 
| 15 
|
6 
| 16 
|
7 
| 17 
|
8 
| 18 
|
9 
| 19 
|
10 
| 20 
|
ЗАДАНИЕ 4
Вычислите пределы:
а)
1 
| 11 
|
2 
| 12 
|
3 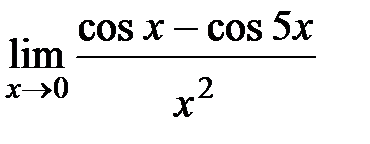
| 13 
|
4 
| 14 
|
5 
| 15 
|
6 
| 16 
|
7 
| 17 
|
8 
| 18 
|
9 
| 19 
|
10 
| 20 
|
б)
1 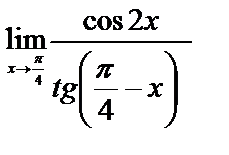
| 11 
| ||||||||
2 
| 12 
| ||||||||
3 
| 13 
| ||||||||
4 
| 14 
| ||||||||
5 
| 15 
| ||||||||
6 
| 16 
| ||||||||
7
Популярное: Почему человек чувствует себя несчастным?: Для начала определим, что такое несчастье. Несчастьем мы будем считать психологическое состояние... Как вы ведете себя при стрессе?: Вы можете самостоятельно управлять стрессом! Каждый из нас имеет право и возможность уменьшить его воздействие на нас...  ©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (2237)
|
Почему 1285321 студент выбрали МегаОбучалку... Система поиска информации Мобильная версия сайта Удобная навигация Нет шокирующей рекламы |
(0.01 сек.)

