 |
Главная |
Задание 6. Вычислить криволинейный интеграл первого
|
из
5.00
|
рода от функции f (x , y) по длине дуги L
уравнениям y = 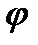 (х) , a
(х) , a 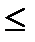 x
x 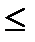 b
b
6.1 f (x , y)= x 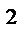 ; L : y=ln x ; 1
; L : y=ln x ; 1 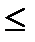 x
x 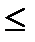 2
2
6.2 f (x , y) = y ; L : y  = 2x от точки А(0;0)
= 2x от точки А(0;0)
до точки В(2; 2)
6. 3 f (x , y) = 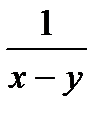 ;L : отрезок прямой
;L : отрезок прямой
соединяющий точки
A( 0;-2) и B (4;0)
6.4 f (x , y) = x + y ;L : граница треугольника с
вершинами A(1;0) , B(0;1)
6.5 f (x , y) =  ;L : -отрезок прямой
;L : -отрезок прямой
соединяющий точки
О (0;0) и A(1;2)
6.6 f (x , y) = x+2y ;L : отрезок прямой от
точки A(1;1) до точки B(5;3)
6.7 f (x , y) = 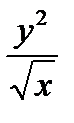 ;L : y
;L : y  =
= 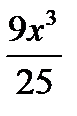 - от точки
- от точки
A(0;0) до точки B(1;0,6)
6.8 f (x , y) =  ;L : отрезок прямой
;L : отрезок прямой
соединяющий точки A(-1;0)
и B (2;0)
6.9 f (x, y) = 2x-y ;L : отрезок прямой
соединяющий точки
A(2;2) и B(1;-3)
6.10 f (x, y) = 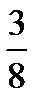 x
x 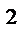 ;L : y =
;L : y = 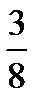 x
x  , 0
, 0 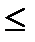 x
x 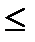 4
4
6.1 1 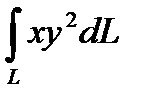 ;L : контур параллелограмма с
;L : контур параллелограмма с
вершинами A(0,1) , B(3,0) ,
C(3,2) , D(0,2)
6.12  ;L : окружность x
;L : окружность x  + y
+ y 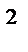 + z
+ z  = a
= a 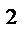
x + y + z = 0
6.13  ;L : контур треугольника с
;L : контур треугольника с
вершинами A(0,0) , B(1,0) , C(0,1)
6.14  ; L : x
; L : x 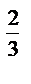 + y
+ y 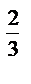 = a
= a  , x
, x  0, y
0, y  0
0
6.15 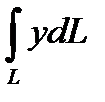 ;L : дуга x
;L : дуга x  + y
+ y 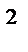 = x
= x  - y
- y 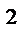 ; x
; x  0 , y
0 , y  0
0
Задание 7. Вычислить поверхностные интегралы
первого рода 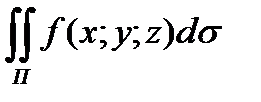 по
по
указанным поверхностям :
7.1П : плоскость x + 2y +3z = 6 , лежащая в 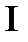 октанте f(x ,y ,z) = 6x + 4y + 3z
октанте f(x ,y ,z) = 6x + 4y + 3z
7.2П : y =  , отсеченная плоскостями x = 0 ,
, отсеченная плоскостями x = 0 ,
x = a ;f(x ,y, z) = x 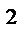 + 3y
+ 3y  + z
+ z 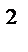 + 5
+ 5
7.3П : часть плоскости x + y + z =a , лежащая в 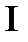 октанте f(x,y,z) = 1
октанте f(x,y,z) = 1
7.4П : z =  ,отсеченная плоскостями y = 0 , y = 5 f(x,y,z) =
,отсеченная плоскостями y = 0 , y = 5 f(x,y,z) = 
7.5П : часть плоскости 6x + 4y + 3z = 12 , лежащая в
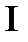 октанте , f(x,y,z) = z + 2x +
октанте , f(x,y,z) = z + 2x + 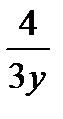
7.6П : z =  , отсеченная плоскостью z =3 ;
, отсеченная плоскостью z =3 ;
f(x,y,z) = xyz
7.7П : часть плоскости x + y + z =1 , лежащая в 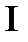
октанте , f(x,y,z) = 2x + y - 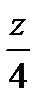
7.8П: граница тела 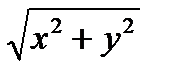
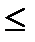 z
z 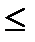 1; f(x,y,z) =x
1; f(x,y,z) =x  + y
+ y 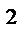
7.9П : часть плоскости 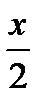 +
+  +
+ 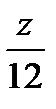 = 1 , лежащая в
= 1 , лежащая в 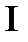 октанте f(x,y,z) = x
октанте f(x,y,z) = x 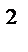 + y
+ y 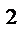 + z
+ z 
7.10П : часть плоскости 6x + 4y + 3z = 12 , лежащая в  октанте f(x,y,z) = z + 2x +
октанте f(x,y,z) = z + 2x + 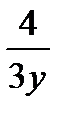
7.11 П : полусфера z =  ; f(x,y,z) = x
; f(x,y,z) = x
7.12 П : поверхность параболоида вращения
z =  (x
(x  + y
+ y 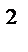 ) , ограниченная плоскостями z =0 ,
) , ограниченная плоскостями z =0 ,
z = 2 ;f(x,y,z) = x 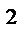 + y
+ y 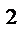
7.13 П : коническая поверхность z 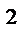 = x
= x  + y
+ y 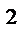 ,
,
ограниченная плоскостями z = 0 , z = 1 ,
f(x,y,z) = x  + y
+ y 
7.14П : поверхность параболоида вращения
z = 1- x 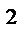 - y
- y  , ограниченная плоскостями z =0 ,
, ограниченная плоскостями z =0 ,
z =1 ;f(x,y,z) = 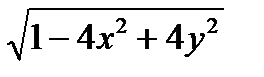
7.15П : часть поверхности конуса x 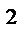 + y
+ y  = z
= z 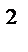 ,
,
0 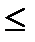 z
z 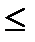 1 ;f(x,y,z)=
1 ;f(x,y,z)= 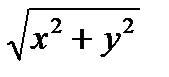
Задание 8. Вычислить поверхностные интегралы
Второго рода
8.1  по верхней стороне
по верхней стороне
части плоскости 2x + 3y + z = 6 лежащей в 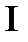 октанте
октанте
8.2 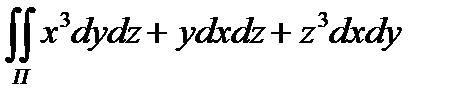 по положительной
по положительной
стороне куба , составленного плоскостями x = 0 ,
y = 0 ,z = 0 , x =1, y =1 , z =1
8.3 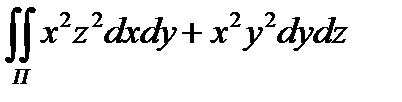 по внешней стороне
по внешней стороне
поверхности , составленной плоскостями x = 0 , y =0
z = 0 ,x + y + z = 1
8.4 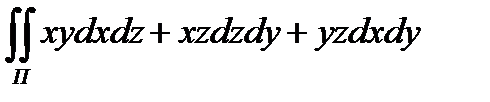 по внешней
по внешней
поверхности , расположенной в 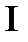 октанте и
октанте и
составленной из плоскостей x = 0 , y =0 , z =0 , z = h
и цилиндра x 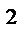 + y
+ y  =R
=R 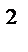
8.5  по верхней стороне части
по верхней стороне части
поверхности z = 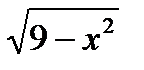 , отсеченной плоскостями
, отсеченной плоскостями
y = 0 ,y =2
8.6 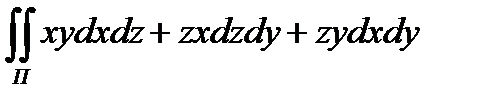 по положительной
по положительной
стороне куба , составленного плоскостями x = 0 ,
y = 0 ,z = 0 , x =1, y =1 , z =1
8.7  по внутренней стороне
по внутренней стороне
части поверхности x 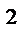 = 4y , отсеченной
= 4y , отсеченной
плоскостями y = 4 , z = 0 , z = 3
8.8 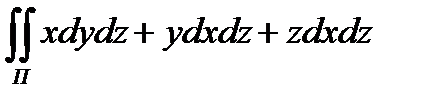 по положительной
по положительной
стороне куба , образованного плоскостями x =0 ,
y = 0 ,z = 0 , x =3 , y = 3 , z = 3
8.9 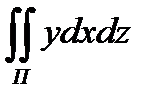 по верхней стороне части плоскости
по верхней стороне части плоскости
x + y + z = a , лежащей в 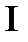 октанте
октанте
8.10  по верхней стороне
по верхней стороне
треугольника , образованного пересечением
плоскости x + y + z =1 cкоординатными
плоскостями
8.11 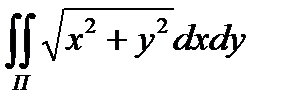 по нижней стороне круга
по нижней стороне круга
x 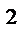 + y
+ y 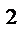
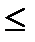 R
R 
8.12 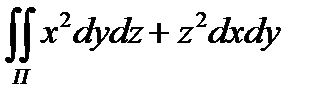 по нижней стороне части конуса x
по нижней стороне части конуса x  + y
+ y  = z
= z  , 0
, 0 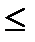 z
z 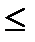 1
1
8.13 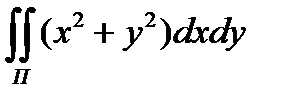 по нижней стороне круга
по нижней стороне круга
x  + y
+ y 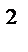 = R
= R 
8.14 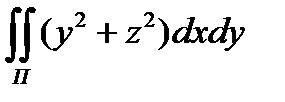 по верхней стороне цилиндрической поверхности z
по верхней стороне цилиндрической поверхности z  = 1 - x
= 1 - x 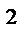 , 0
, 0 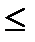 y
y 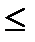 1
1
8.15 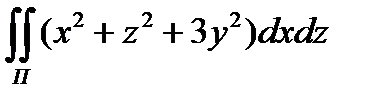 по внешней стороне части
по внешней стороне части
|
из
5.00
|
Обсуждение в статье: Задание 6. Вычислить криволинейный интеграл первого |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

