 |
Главная |
Решение систем линейных уравнений методом Гаусса
|
из
5.00
|
Матрицы. Основные понятия
Матрицей размерности (m*n) называется совокупность чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов.





Действия над матрицами и их свойства




Вычисление определителей второго и третьего порядка. Свойства определителей.


Минор некоторого элемента определителя. Алгебраическое дополнение некоторого элемента определителя. Вычисление определителей высоких порядков.

Любой определитель n-го порядка можно вычислить на основании следующей теоремы.
Теорема 1. Определитель n-го порядка равен сумме произведений элементов любой его строки (столбца)
на их алгебраические дополнения.
Замечание1: Вычисление определителя по данной теореме называют разложением определителя по
элементам строки или столбца (далее-ряда).
Метод понижения порядка определителя:
Этот метод также основан на элементарных преобразованиях определителя.
1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.
2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.
Обратная матрица. Алгоритм вычисления обратной матрицы.

Ранг матрицы. Свойства ранга матрицы. Метода окаймления миноров и метод элементарных преобразований нахождения ранга матрицы.



Системы линейных уравнений. Основные понятия.
Системой линейных уравнений называют конечную совокупность линейных уравнений относительно неизвестных  .
.
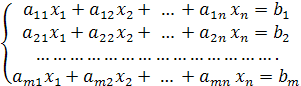
где числа  (
( 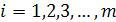 и
и 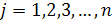 ) называются коэффициентами, числа
) называются коэффициентами, числа  i – свободными членами системы линейных уравнений.
i – свободными членами системы линейных уравнений.
Решением системы уравнений называют такой упорядоченный набор чисел  , который является решением каждого уравнения системы.
, который является решением каждого уравнения системы.
Решить систему уравнений – значит найти все ее решения или убедиться в том, что их нет.
Совместной называется система уравнений, которая имеет хотя бы одно решение.
. Система уравнений является либо несовместной (не имеет ни одного решения), либо определенной (имеет единственное решение), либо неопределенной (имеет бесконечное множество решений). В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Две системы линейных уравнений называют равносильными (эквивалентными), если они имеют одни и те же решения.
Решение системы уравнений методом обртной матрицы и методом Крамера.


Решение систем линейных уравнений методом Гаусса.
|
из
5.00
|
Обсуждение в статье: Решение систем линейных уравнений методом Гаусса |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

