Предмет, задачи теории игр

Теория игр – раздел математики, применяемый в социально-экономических, политических, организационных, экологических процессах. Практически все аспекты человеческой деятельности затрагивают в той или иной степени интересы разных сторон и поэтому относятся к области теории игр. Однако в настоящее время методы теории игр в реальных процедурах управления (в первую очередь при управлении предприятиями и организациями, построении организационных систем, формировании хозяйственного механизма, при социально-экономическом планировании и прогнозировании) широко не используются. Это можно объяснить как отсутствием теоретико-игровой подготовки у специалистов по управлению, так и тем, что классические игровые модели слишком абстрактны и с трудом адаптируются к реальным процессам управления и принятия решений. Также в настоящее время существуют трудности, связанные с недостатком необходимой литературы по теории игр.

Итак, слово «игра» применяется для обозначения некоторого набора правил и соглашений, составляющих данный вид игры, например, игра в шахматы, волейбол и т. д. Иначе, теория игр – это наука об оптимальном разрешении конфликтов между субъектами интересов или согласовании интересов между ними. Согласно Н.Н. Воробьеву [3], под конфликтом будем понимать всякое явление, применительно к которому можно говорить, кто и как в этом явлении участвует, каковы могут быть у этого явления исходы, кто в этих исходах заинтересован и в чем заключается эта заинтересованность.Ход событий в конфликте зависит от решений, принимаемых каждой из сторон, и поэтому поведение любого участника конфликта, если оно разумно, должно определяться с учетом возможного поведения всех его участников. Для конфликта характерно то, что ни один из его участников заранее не знает решений, принимаемых остальными участниками, т. е. вынужден действовать в условиях неопределенности. Неопределенность зависит не только от сознательных действий других участников, но и от действий тех или иных «стихийных сил» (непознанной природы). Конфликт может возникнуть также из-за различия целей, отражающих не только несовпадающие интересы различных сторон, но и множественные интересы одной из них [14].

Формализация содержательного описания конфликта представляет собой его математическую модель – игру. Участников конфликта называют игроками. При этом в качестве единого игрока может выступать целый коллектив, имеющий некоторые общие интересы (фирма, предприятие, отдел, цех и т. д.).

Вопрос о принятии оптимальных решений в условиях конфликта весьма сложен. Одним из путей преодоления возникающих в данном случае трудностей является математизация всей проблемы, т. е. четкая и по возможности количественная формулировка задач и их решение математическими (теоретико-игровыми) методами.

«Игрой в теории игр называется схематизированная и приспособленная для математического изучения модель конфликта», – так считает Воробьев Н.Н. При этом, разумеется, игра должна сохранять все основные, существенные черты моделируемого конфликта. Прежде всего, в игре должны быть отражены характеристики («компоненты») конфликта:

1) участвующие в конфликте стороны (игроки);

2) решения, которые игроки могут принимать (стратегииигроков);

3) степень осуществления целей каждого игрока в ситуации, которая складывается в результате выбора игроками своих стратегий (выигрыши игроков в соответствующих ситуациях).

Функция, ставящая в соответствие каждой ситуации выигрыш игрока, называется функцией выигрыша этого игрока.

Точное описание множества игроков, множеств стратегий для каждого игрока, а также их функций выигрыша и составляет задание игры. Игры, заданные в таком виде, обычно называются играмив нормальной форме.

Игроком не обязательно является отдельное физическое лицо; игрок – это сторона, отстаивающая единые интересы, поэтому игроком может быть предприятие, фирма, корпорация. Иногда для удобства в качестве игрока принимается природа, формирующая обстоятельства, в которых приходится принимать решения.

Решениями игрока, его стратегиями являются по существу не сами выбираемые игроком действия, а правила их выбора в зависимости от обстоятельств, в которые попадает игрок к моменту принятия решения. Принимающий решение субъект руководствуется тем, что он знает (или хотя бы думает, что знает) об обстановке. Но информация может быть неполной, неточной, недостаточной, т. е. знания его не всегда исчерпывающи. Игрок может знать только свою часть информации, но ситуация в игре складывается из действий всех игроков. Такая группа неразличимых физических состояний игрока называется его информационным состоянием.

Стратегия игрока является правилом выбора некоторого действия в каждом информационном состоянии, или, выражаясь математически, стратегия игрока есть функция, определенная на множестве всех его информационных состояний, значения которой суть действия, доступные в соответствующем информационном состоянии.

Основная терминология была принята создателями теории игр Дж. фон Нейманом и О. Моргенштерном («Теория игр и экономическое поведение»).

Принятие оптимальных решений в условиях конфликта должно начинаться с выяснения того, что именно следует понимать под оптимальностью. Это первый основной вопрос теории игр.

Далее, когда принцип оптимальности выбран, т. е. установлено, какими свойствами должны обладать ситуации, чтобы считаться достаточно разумными, выгодными, справедливыми, словом, «оптимальными» исходами игры, необходимо убедиться в существовании таких ситуаций, т. е. в реализуемости выбранного принципа оптимальности. Это второй основной вопрос теории игр. Возможна ситуация, когда принцип оптимальности не имеет реализаций в данной игре и оказывается в подобном случае чисто утопическим.

Вычисление, фактическое нахождение решений (реализаций) становится третьей, основной задачей теории игр.

В теории игр изучается оптимальное поведение игроков в играх, обеспечивающее согласование их интересов.

Итак, игра Г, как уже упоминалось, считается заданной, если указаны:

1) все игроки: 1, 2, … n;

2) множества стратегий игроков: S₁, S₂, … S_n;

3) функции выигрыша для каждого из игроков H₁, H₂, … H_n, определенные для каждой ситуации.

Партию игры Г можно представить себе так:

игроки 1, 2, … n независимо друг от друга выбирают свои стратегии s₁, s₂, … s_n, создавая тем самым ситуацию (s₁, s₂, … s_n), после чего каждый игрок из некоторого источника получает причитающийся ему в этой ситуации выигрыш.

Из сказанного следует, что целью каждого игрока в любой игре должно являться достижение такой ситуации, при которой значение его функции выигрыша будет максимальным. Необходимо подчеркнуть, что выигрыш игрока в некоторой ситуации содержит всестороннюю ее оценку.

Однако выбор ситуации зависит от совместных действий всех участников, а каждый отдельный игрок может влиять на формирование игры лишь частично. При этом, ввиду различия интересов игроков, каждый из них будет стремиться повернуть ход событий в свою пользу, добиваясь создания ситуации, выгодной лично ему. Но выбор критерия разумности поведения игроков в игре является первой из основных задач теории игр.

Необходимым признаком разумности намерений и действий игрока является осуществимость этих намерений и, следовательно, результативность соответствующих действий. Следовательно, каждый игрок должен стремиться к такой ситуации, которая фактически может сложиться во время игры.

Общепринятым аналогом оперирующей стороны является лицо, принимающее решение (ЛПР). Соответствующими специалистами осуществляется исследование в интересах оперирующей стороны. Он преследует ту же цель, но сам, как правило, не принимает окончательного решения, а дает научно обоснованные рекомендации, т. е. проводит качественный и количественный анализ и обосновывает целесообразность принятия тех или иных решений. Ответственность за принятие возлагается на оперирующую сторону.

Исследователь операций и оперирующая сторона могут иметь различную информацию, так как во время анализа предстоящей операции и ее проведения информация может меняться, поступать в динамике. Кроме того, время для исследований может быть также различно.

Совпадение интересов оперирующей стороны и исследователя операций должно быть основано на хорошо построенном организационно-экономическом механизме, что побуждает исследователя операций поддерживать именно те цели, которые преследует оперирующая сторона.

Как отмечалось ранее, конфликт содержит в себе следующие компоненты: перечень субъектов, участвующих в конфликте; определение множеств их выборов; интересы (мотивы), определяющие выбор.

Кроме того, при моделировании конфликта очень важно описать информационную обстановку, т. е. всю информацию, которая уже имеется у субъектов конфликта и может поступать со временем. Также необходимо учитывать возможность обмена информацией, добывания ее и добровольной передачи информации одним субъектом другому. Математическая модель конфликтной ситуации называется игрой. Таким образом, теория игр – это математическая теория принятия решений в условиях конфликта. Из этого определения следует, что теория игр есть важная часть теории исследования операций, изучающая вопросы принятия решений в конфликтных ситуациях.

Важной задачей игр является не описание, а разрешение конфликтов, т.е. принятие компромиссных взаимовыгодных решений, которые полностью или хотя бы частично согласовывали интересы всех взаимодействующих сторон.

Если удается формализовать (смоделировать) конфликт и определить принцип оптимальности, т. е. принцип выбора оптимального решения в игре, то получается математическая задача, которую можно решать математическими методами, без учета ее содержательной постановки.

В теории игр используется разнообразный и хорошо разработанный математический аппарат (теория множеств, теория вероятностей, топология, теория функций, теория дифференциальных уравнений, методы оптимизации, вариационное исчисление, динамическое программирование, оптимальное управление и др.). Однако математические модели теории игр (теоретико-игровые модели) имеют свою специфику. Они описывают процесс принятия решений, которые трудно формализовать.

В этой связи в рамках теории игр развивается специфический математический аппарат, обеспечивающий моделирование процессов принятия решений в сложных социально-экономических, политических и прочих конфликтах. При этом возникают новые ранее не изученные математические задачи.

 

Анализ возможностей приложения теории игр важен по той причине, что при моделировании конфликтных ситуаций, например процессов принятия решений в сложных социально-экономических системах, трудность вызывает формализация мотивации поведения самой системы.

 

Как уже было сказано, предмет исследования теории игр – математические модели принятия оптимальных решений в конфликтных ситуациях. Формальное описание принятия решений следует разбить на две части:

 

1) математическая модель конфликтной ситуации, или игра, — описание конфликтной ситуации, включающее в себя описание субъектов, принимающих решения, их возможностей и интересов;

2) принцип оптимальности – описание правил рационального поведения игроков.

 

Оптимальность и неоптимальность того или иного исхода конфликта зависит от интересов и возможностей его участников. В этом смысле принцип оптимальности является функцией игры. Можно рассматривать различные принципы оптимальности, но если один из них выбран, то для каждой игры можно однозначно указать множество ее рациональных исходов.

 

Математическая модель конфликта и принцип оптимальности дают полное описание принятия решений в условиях конфликта.

Задать игру можно различными способами. Возможно воспользоваться нормальной формой описания игр. В описании игры можно выделить следующие элементы:

1) коалиции действий – совокупность действующих совместно в данной конфликтной ситуации субъектов;

2) коалиции интересов – множество одинаково заинтересованных в исходе конфликта сторон;

3) множества возможных выборов каждой из коалиций действия;

4) описание предпочтений каждой из коалиций интересов;

5) множество возможных исходов конфликта.

Появление слова «коалиция» указывает на тот факт, что участниками конфликта могут быть не только отдельные лица, но и большие, сложно организованные группы лиц. Коалиции действия и интересов могут не совпадать. Например, пассажиры самолета бывают заинтересованы в его скорейшем прибытии к месту назначения и, таким образом, образуют коалицию интересов, однако они не могут предпринять никаких действий, направленных на достижение этой цели, т. е. не являются коалицией действия. Если коалиция действия совпадает с коалицией интересов, то подобную монолитную коалицию можно считать одним лицом, поэтому ее называют игроком. Если все коалиции действия совпадают с соответствующими коалициями интересов, то игру называют бескоалиционной, а ее участников – игроками.

Для принятия решений необходимо владеть определенной информацией. При этом как сам выбор из множества стратегий, так и ожидаемый результат зависят в значительной степени от информации, которой владеет игрок к моменту принятия решения: речь идет о вариантах выбора, мотивах поведения или принципе оптимальности игроков, о природных неопределенных факторах, о той информации, которой в данный момент игрок не имеет, но которая будет поступать к нему.

Далее необходимо выяснить условия, которым должна удовлетворять ситуация (именно к данной ситуации будут стремиться игроки при выборе своих стратегий).

Пусть ситуации и отличаются друг от друга только стратегиями первого игрока, причем < (вторая ситуация для первого игрока предпочтительнее). В этом случае, если игрок I выяснит, что дело идет к выбору игроками 2, … n стратегий s₂, …, s_n соответственно, то не станет выбирать стратегии s₁, а предпочтет стратегию sⁱ₁.Следовательно, намерения игроков 2, … n достичь ситуации s неосуществимы, и разумными их считать нельзя. Таким образом, игрок I препятствовал в данном случае созданию ситуации s.

Следовательно, для того чтобы ситуация могла стать целью разумно действующих игроков, ей необходимы следующие свойства:

;

;

…

.

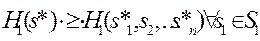Ситуации, обладающие указанными свойствами, носят название ситуаций равновесия. Такие ситуации могут складываться в результате разумного выбора игроками своих стратегий. Также только такие ситуации могут быть зафиксированы игроками в договорах между ними [14].

Классификации игр

Таким образом, для описания конфликтной ситуации необходимо задать систему

,

где N – множество игроков; K_g – множество коалиций действия; K_и – множество коалиций интересов; S_i – множество выборов коалиции i из Kg; h_j – функция выигрыша коалиции j из K_и; L – множество возможных исходов игры.

Игры бывают статическими и динамическими.

Можно привести различные классификации игр. Рассмотрим основные классы теоретико-игровых моделей.

В качестве первого классификационного признака возьмем число игроков. Различают игры двух лиц и игры n лиц (n>2). Игры двух лиц называются антагонистическими, если игроки преследуют противоположные цели. Подробнее антагонистические игры описаны в работе [14].

Антагонистические игры происходят не только при описании конфликтов наподобие военных, но и при описании игры с природой, когда исследователь операции или оперирующая сторона проявляет осторожность, принимая решения в условиях неопределенности.

Существуют также неантагонистические игры двух лиц ( ).

Другой принцип классификации связан с вопросом о допустимости образования тех или иных коалиций. Если в игре образование коалиций недопустимо, то такая игра называется бескоалиционной и определяется заданием множества игроков, пространств их стратегий и набором их функций выигрыша.

К бескоалиционным играм могут быть отнесены также игры, где . В истинно коалиционных играх разрешены такие коалиции, где 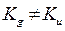. Среди подобных игр наиболее распространены кооперативные игры, в которых образуется одна коалиция. Целью этой коалиции является максимизация суммарного выигрыша, с тем чтобы впоследствии разделить его между членами коалиции по соглашению.

Отдельный класс составляют игры с бесконечным числом игроков.

Следующим признаком классификации могут являться стратегии. Если множество стратегий всех игроков конечно, то игра называется конечной.

Когда хотя бы одно из множеств S_i, , бесконечно, игра называется бесконечной. Для теоретического анализа более удобны конечные игры, имеющие меньшую практическую ценность, чем бесконечные.

Игры можно квалифицировать и в соответствии с формой их задания.

При этом различают позиционные игры и игры в нормальной форме. Если процесс принятия решений описывается в виде динамического, где игроки выбирают свои стратегии последовательно по шагам, обладая при этом определенной информацией при каждом шаге выбора стратегии, то такие игры называются позиционными (гл. 3). Классическим примером такой игры являются шахматы. Если в динамических играх конфликт моделируется дифференциальными уравнениями, то такие игры называют дифференциальными. Если в игре стратегия представлена как одноактный выбор, то такая игра считается заданной в нормальной форме.

Интерес представляют игры с непрерывными функциями выигрышей: классы выпуклых, вогнутых, выпукло-вогнутых игр.

Кроме упомянутых классов, существует множество их модификаций.

Исходные элементы множества S_i называются чистыми стратегиями, а их произвольная выпуклая комбинация (мера) — смешанной стратегией.

Существует два способа реализации смешанных стратегий:

1) введение искусственной рандомизации, т. е. использование функции распределения на исходном множестве управлений;

2) введение повторения, т. е. проведения конфликта многократно.

При этом с определенной частотой выбирают некоторые элементы исходного множества. В обоих способах соответствующим образом определяются функции выигрыша.

Таким образом, рассматриваемые в теории игр объекты, т. е. игры, разнообразны. Далее будем рассматривать примеры, иллюстрируя их теоретическим материалом. В качестве примеров будут рассмотрены различные классы игр, применяемые в них принципы оптимальности и их реализации.

Постановка задачи

Продукты или услуги, предлагаемые компаниями на рынке, можно сравнивать и упорядочивать не только по таким объективным характеристикам, как, например, цена, качество и тому подобное, по их популярности, по тому, какой предпочтительнее. Компании, учитывая предпочтения покупателей, предлагают свои продукты или услуги в соответствии с требованиями рынка. При этом различные группы потребителей в отношении одних и тех же продуктов или изделий могут иметь различные предпочтения.

Исследуем компании, упорядочивающие по степени важности для их бизнеса предлагаемые четыре вида программного обеспечения: программное обеспечение для ведения бухгалтерского учета первого вида БПО₁ (направленности, например, для малых предприятий), программное обеспечение для ведения бухгалтерского учета второго вида (БПО₂), программное обеспечение для управления складскими запасами первого вида (СПО₁) и программное обеспечение для управления складскими запасами второго вида (СПО₂). Предположим, что по данным проведенного обследования некоторый контингент потенциальных клиентов оказался разделенным на четыре группы, установившие порядки предпочтения, описываемые таблицей 1.1.

Таблица 1.1

Номер группы	Предпочтительность по порядку для группы
	СПО2, БПО2, СПО1, БПО1 БПО2, СПО1, БПО1, СПО2 СПО1, БПО1, СПО2, БПО2 БПО1, СПО2, БПО2, СПО1

 

Пусть при этом оказалось, что группы потенциальных покупателей, придерживающихся порядков предпочтения 1, 2, 3 и 4, составляют соответственно 10, 20, 30 и 40 процентов от общего числа покупателей, а покупатели, выбравшие иные порядки предпочтения, отсутствуют. (Подчеркнем, что эти предположения составляют условия задачи, и будем соблюдать их при ее решении.)

Можно ли в описанных условиях устанавливать какое-либо разумное упорядочение по предпочтению для рассматриваемого нами контингента покупателей в целом? Можно ли хотя бы выбрать программное обеспечение, разработка которого удовлетворила бы покупателей в наибольшей степени?

Пусть проведено голосование «на лучшее программное обеспечение» (по функциональности для конкретного пользователя, цене, пользовательскому интерфейсу и т. д.). По правилу относительного большинства перевес, очевидно, даст БПО₁, которое соберет 40 % голосов. Ближайший конкурент, СПО₁, соберет лишь 30 % голосов.

 

Однако сторонники СПО₁ могут поставить на голосование вопрос: какое программное обеспечение из двух лучше, БПО₁ или СПО₁? Из табл. 1.1 порядков видно, что за СПО₁ при сравнении с БПО₁ будут голосовать 1, 2 и 3-я группы, и всего за это программное обеспечение будет подано 60 % голосов против 40 %, поданных за БПО₁. Далее нам понадобится рассматривать различные голосования такого типа, поэтому для удобства читателей мы вычислим впрок результаты и сведем их в «турнирную» таблицу 1.2.

Таблица 1.2

	БПО1	СПО1	БПО2	СПО2
БПО1	Х	40 %	70 %	90 %
СПО1	60 %	Х	30 %	50 %
БПО2	30 %	70 %	Х	20 %
СПО2	10 %	50 %	80 %	Х

 

Но борьба мнений может и не ограничиться сравнением СПО₁ с БПО₁. Покупатели, предпочитающие БПО₂, могут потребовать сравнения голосованием своего фаворита с только что победившим СПО₁. В этом голосовании 1, 3 и 4-я группы, составляющие 70 % голосов, выскажутся за БПО₂ и лишь 30 % за СПО₁.

 

Но и БПО₂ нельзя считать окончательным победителем. При его сравнении голосованием с СПО₂ в пользу БПО₂ выскажутся лишь 20 % покупателей, а за СПО₂ – все остальные, т. е. 80 %.

Наконец, сравнение СПО₂ с самым первым фаворитом, БПО₁, приводит к уверенной победе последнего: 90 % против 10 %. Но тогда сложится ситуация, когда снова не согласятся приверженцы СПО₁, и вся история повторится сначала.

Таким образом, определение лучшего варианта путем последовательных голосований может приводить к противоречиям. Это несколько неожиданное явление было обнаружено еще в XVIII веке; его исследовал Кондорсе.

В данной ситуации не прояснит вопроса о «лучшем» программном обеспечении и попытка осуществить голосование по так называемой «олимпийской» системе. Из табл. 1.2 видно, что при объединении «в предварительные подгруппы» программного обеспечения, не имеющего общих признаков, мы получаем следующую схему розыгрыша:

Если же в предварительные подгруппы объединить программное обеспечение по признаку «направленность» (бухгалтерия и склад), то картина будет иной:

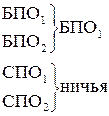
При этом никакие «перебаллотировки» последнего «ничейного» счета не изменят, ибо он связан не со случайностями борьбы, а с зафиксированными мнениями голосующих. Мы интересуемся как раз выбором «лучшего», по мнению покупателей, программного обеспечения на основе этого мнения.

Наконец, объединение программного обеспечения в предварительные группы по их номеру (1 и 2) дает нам победу БПО₁ в полуфинале бухгалтерского программного обеспечения и ничью в полуфинале складского программного обеспечения. Как отмечалось ранее, ничья сама по себе «неразрешима». В этой связи напрашивается вывод: сравнивать БПО₁ последовательно с обеими системами программного обеспечения для склада (то обстоятельство, что при этом одна из рассматриваемых систем программного обеспечения участвует в большем числе сравнений, чем другие, не изменит в отличие от многих спортивных состязаний их шансов на победу; мы предполагаем, что в результате голосования относительные преимущества программных обеспечений не изменяются). Но исход в этом случае будет опять-таки зависеть от порядка сравнений:

Попытаемся определить победителя среди рассматриваемых систем программного обеспечения, используя табл. 1.2, как будто она является таблицей матч-турнира, а приведенные в ней проценты суть очки, полученные программным обеспечением при его сравнении с каждым из остальных. Будем определять победителя по сумме набранных очков.

При таком подсчете БПО₁ займет I место с 200 очками, обе СПО разделят II – III места со 140 очками каждая, а на последнем, IV, месте будет БПО₂, набравшее лишь 120 очков.

Вспомним, однако, что цель наших рассуждений принципиально отличается от рассмотрения таблицы реального матч-турнира, скажем, шахматистов. В данном случае речь идет об определении победителя в некотором совершенно определенном виде соревнования (в условия которого входят и жеребьевка, определяющая очередность встреч, и временной регламент ходов в каждой партии, и, наконец, календарное расписание туров), а вовсе не об объективном присуждении титула «лучшего шахматиста» среди участников турнира или матч-турнира. Здесь мы как раз заинтересованы в определении лучшего программного обеспечения, а отнюдь не того, которое соберет наибольшее число очков по тем или иным нами же придуманным правилам.

После подведения итогов такого турнира видно, что БПО₂ оказалось явным «аутсайдером», и поэтому исключим его из дальнейшего рассмотрения, а будем сравнивать оставшиеся системы программного обеспечения в следующем турнире. Таблица этого турнира получается из табл. 1.2, если вычеркнуть из нее строку и столбец, соответствующий БПО₂. В этом турнире победителем по-прежнему будет БПО₁ с 130 очками, II место достанется СПО₁ со 110 очками, а на последнем месте окажется СПО₂, у которого будет только 60 очков. По итогам второго турнира следует отбросить СПО₂ и определить окончательного победителя в третьем турнире (фактически это будет уже матч) с участниками БПО₁ и СПО₁. Но в нем победу одержит СПО₁, что, однако, противоречит результатам первых двух турниров.

Итак, в условиях заданных различных предпочтений обычные подходы к определению наилучшего программного обеспечения могут и не привести к цели. Это свидетельствует о том, что может оказаться полезной модификация самого понимания «наилучшего», «оптимального». Возможна, например, следующая точка зрения.

Поставим вопрос о том, выбор какого программного обеспечения или каких нескольких систем программного обеспечения естественно считать наилучшим, оптимальным.

Во-первых, среди этих систем программного обеспечения (если их несколько) не должно быть предпочитаемых. Данное свойство выбранного множества систем программного обеспечения назовем его внутренней устойчивостью. По существу оно означает, что после оптимального выбора противопоставление хорошего лучшему должно быть исключено.

Во-вторых, каждое программное обеспечение из числа тех, которые мы не сочли оптимальными, должно предпочитаться некоторому программному обеспечению из числа выбранных (оптимальных). Это свойство выбираемого множества называется его внешней, устойчивостью (всякому отклонению от установленного оптимума можно противопоставить вариант, данному оптимуму принадлежащий).

Подобные «оптимальные множества», обладающие свойствами внутренней и внешней устойчивости, встречаются во многих разделах математики (имея различные названия). В теории игр их принято называть решениями по Нейману – Моргенштерну или Н-М-решениями (Воробьев Н.Н.).

В случае рассматриваемой задачи Н-М-решение состоит в выборе обеих СПО: внутренняя устойчивость этой пары систем программного обеспечения проявляется в цифрах 50 % и 50 % турнирной таблицы, а внешняя – в том, что альтернативе в виде БПО₁ успешно будет противостоять СПО₁, а альтернативе в виде БПО₂ – СПО₂. Иных Н-М-решений в этой задаче быть не может, так как нет других внутренне устойчивых пар (единственное программное обеспечение должно было качественно превосходить каждое из остальных). Такого программного обеспечения, как мы видели, в условиях нашей задачи нет [3].

Рассмотренный выше вопрос о том, какое программное обеспечение является наилучшим, лишен смысла, так как необходимо пояснить, какое содержание вкладывается в само понятие оптимальности. Но во «Введении» было сказано, что в этом и состоит первый основной вопрос теории игр.