 |
Главная |
Антагонистическая игра с полной информацией
|
из
5.00
|
Пусть описанное выше сравнение систем программного обеспечения было проведено экспертами, где две компании-разработчика ПО под названиями «Чайка» и «Сокол» осуществляют оригинальные разработки систем программного обеспечения. Компания «Чайка» специализируется на разработке БПО, а компания «Сокол» − на разработке СПО, что ограничивает планы этих компаний программными продуктами соответствующего направления. Каждая компания может разработать программный продукт в одном из двух вариантов, причем себестоимость и продажная цена всех четырех видов программных продуктов одинаковы. Одновременная же разработка компанией программного продукта в двух вариантах с самого начала признана экономически невыгодной и поэтому не рассматривается. Введем ограничение: ПО будет внедряться в пределах исследуемого региона. В исследуемом регионе, как установили социологи и специалисты по прогнозированию спроса, найдет сбыт 1000 систем, разрабатываемых рассматриваемыми компаниями, причем в случае разработки ПО двумя компаниями спрос на них распределится в соответствии с данными табл. 1.2.
Описанное положение дел можно понимать как игру, в которой участвуют два игрока − предприятия «Чайка» и «Сокол», а их выигрыши определяются количеством внедренных систем. Так как по условию общий спрос в регионе на рассматриваемые виды программного обеспечения составляет 1 тыс.шт. (цифры примера условные), суммарный выигрыш обоих предприятий от реализации данных программных продуктов будет постоянен. Подобные игры принято называть играми с постоянной суммой (выигрышей игроков). В играх такого типа всякое увеличение выигрыша одного игрока приведет к уменьшению выигрыша другого, и наоборот. Следовательно, в условиях игры с постоянной суммой никакие совместные выборы стратегий игроками или же соглашения между ними не могут быть полезны обоим игрокам одновременно, поэтому такие игры обычно в теории игр называются антагонистическими. Подчеркнем, что в данном случае понятие антагонизма соответствует наиболее прямолинейному варианту философской категории антагонизма, которая, разумеется, не укладывается в схему «равенства по величине и противоположности по знаку». В этой связи многие противоречия, носящие с философской точки зрения антагонистический характер, не поддаются схематизации в рамках антагонистических игр.
Проанализируем стратегии игроков в рассматриваемой игре. Первостепенное значение имеет информационное состояние игроков (точнее говоря, тех работников предприятий, которые будут принимать решения о выпуске программных продуктов).
Рассмотрим случай различной информированности игроков. Допустим, что руководство предприятия «Сокол» своевременно узнает, какой вид программного продукта намерена выпустить «Чайка». Когда «Чайка» узнает, какой вид программного продукта решила выпустить компания «Сокол», перестраиваться ей будет уже поздно. Опишем стратегии участников игры в этих предположениях. «Чайка» по условию не знает, какое программное обеспечение выпустит «Сокол». Это состояние незнания является ее единственным информационным состоянием. «Чайка» может придерживаться, одного из двух направлений: выпускать БПО1 или БПО2. Очевидно, действия в одном из двух направлений и будут стратегиями предприятия «Чайка». «Сокол» может оказаться в одном из двух информационных состояний:
Информационное состояние 1 – знать, что «Чайка» намерена выпускать БПО1;
Информационное состояние 2 – знать, что «Чайка» намерена выпускать БПО2.
В каждом из этих состояний предприятие выбирает одно из двух направлений: выпускать СПО1 или СПО2. В этой связи всего у предприятия «Сокол» имеется четыре стратегии:
Стратегия 1 – в ответ на БПО1 выпускать СПО1, в ответ на БПО2 – также СПО1;
Стратегия 2 – в ответ на БПО1 выпускать СПО1, а в ответ на БПО2 − СПО2;
Стратегия 3 – в ответ на БПО1 выпускать СПО2, а в ответ на БПО2 − СПО1;
Стратегия 4 – в ответ на БПО1 выпускать СПО2, а в ответ на БПО2 – также СПО2.
Всего в рассматриваемой игре может таким образом сложиться  ситуаций.
ситуаций.
Эти ситуации вместе с выигрышами участников игры в каждой из них естественно расположить в виде табл. 2.2.
В данном случае в верхней строке каждой клетки, соответствующей ситуации, указаны выпускаемые программные продукты, а в нижней строке ‑ «счет» процентов проданных программных продуктов. Ввиду того что из описания стратегий следует, какие программные продукты будут выбраны в каждой ситуации, их перечень можно не помещать в соответствующей клетке.
| БПО1 | СПО1 | БПО2 | СПО2 | |
| БПО1 | Х | 40 % | 70 % | 90 % |
| СПО1 | 60 % | Х | 30 % | 50 % |
| БПО2 | 30 % | 70 % | Х | 20 % |
| СПО2 | 10 % | 50 % | 80 % | Х |
Таблица 2.2
| Стратегии предприятия «Сокол» Стратегии предприятия «Чайка» | БПО1→ СПО1 БПО2→ СПО1 | БПО1→ СПО1 БПО2→ СПО2 | БПО1→ СПО2 БПО2→ СПО1 | БПО1→ СПО2 БПО2→ СПО2 |
| БПО1 | БПО1→ СПО1 40:60 | БПО1→ СПО1 40:60 | БПО1→ СПО2 90:10 | БПО1→ СПО2 90:10 |
| БПО2 | БПО2→ СПО1 70:30 | БПО2→ СПО2 20:80 | БПО2→ СПО2 70:30 | БПО2→ СПО2 20:80 |
Так как стратегии предприятия «Чайка» и «Сокол» были выписаны нами ранее, их можно также не указывать в таблице. Наконец, задание процента проданных программных продуктов предприятия «Чайка» в наших условиях (постоянство сумм!) вполне определяет процент проданных программных продуктов предприятия «Сокол» (в сумме они составляют 100 %), поэтому достаточно указывать только первое из этих чисел. После подобных упрощений наша таблица приобретает вид:
 (2.8)
(2.8)
Очевидно, всякая антагонистическая игра, в которой каждый игрок имеет конечное число стратегий, может быть представлена в таком виде. В связи с этим все антагонистические игры с конечным числом стратегий игроков называются матричными играми, а соответствующие им матрицы ‑ матрицами выигрышей. Формально стратегии предприятия «Чайка» оказываются при этом строками матрицы выигрышей, а стратегии предприятия «Сокол» − ее столбцами. Игрока, выбирающего строки, принято называть «первым игроком» («игрок 1»), а игрока, выбирающего столбцы, ‑ «вторым игроком» («игрок 2»). В матрицах выигрышей матричных игр принято записывать выигрыш именно игрока 1, т. е. ущерб, нанесенный игроку 2 (в данном случае по сравнению с тем положением дел, когда он получал бы все 100 % выигрыша).
Поставим вопрос о наилучших (оптимальных) стратегиях игроков в матричной игре с матрицей выигрышей (2.8).
Если игрок 1, выбирая какую-либо строку матрицы, заинтересован в своем гарантированном выигрыше (например, если он достаточно осторожен), то он должен допускать, что его противник, игрок 2, выбирает тот столбец, на котором эта строка имеет минимальный элемент. Этот минимальный выигрыш и является поэтому его гарантированным выигрышем.
Следовательно, для игрока 1 естественно выбрать такую стратегию − строку, в которой его гарантированный выигрыш максимален. Стремление игрока получить именно максиминный выигрыш является достаточно разумным в антагонистической игре принципом оптимальности.
Максиминная стратегия игрока 1 обладает следующим свойством устойчивости: отклонение игрока от максиминной стратегии не может привести к увеличению его уверенного (гарантированного, минимального) выигрыша, поэтому у игрока 1 нет оснований отклоняться от максиминной стратегии.
Проведем теперь аналогичные рассуждения в отношении игрока 2. Если он выбрал некоторый столбец, то его наибольший ущерб будет равен наибольшему в этом столбце элементу. В связи с этим для игрока 2 естественно выбрать такой столбец, где этот наибольший элемент будет минимальным.
Для игрока 2 оптимальным будет выбор второго столбца матрицы. Заметим, что в данной матрице минимакс оказался равным максимину. Их общее значение называется значением игры. Таким образом, значение игры есть тот выигрыш игрока 1, который он заведомо может получить, а больше которого ему заведомо могут не дать. Так, в значении игры проявляются черты своего рода равновесности.
Минимаксная стратегия игрока 2 устойчива примерно в том же смысле, в каком устойчива максиминная стратегия игрока 1. Именно никакое отклонение игроком 2 от минимаксной стратегии не может уменьшить его возможных потерь.
Очевидно, что в рассматриваемой игре ситуация, образованная выбором первой строки и второго столбца матрицы, такова, что отклоняться от нее невыгодно ни одному из игроков. Это и есть ситуация равновесия. Можно доказать, что для наличия в антагонистической игре ситуации равновесия необходимо и достаточно равенство максимина и минимакса в ее матрице выигрышей, [14].
Понимание ситуации равновесия как такой ситуации, от которой ни одному игроку нецелесообразно отклоняться (в предположении, что остальные игроки сохраняют свои стратегии в соотношении с ситуацией равновесия), позволяет говорить о ситуациях равновесия и в играх, не являющихся антагонистическими, и даже в играх с числом участников больше двух.
Ситуации равновесия и только они могут быть предметом договоров между игроками. Действительно, если игроки договорятся играть так, чтобы получилась ситуация равновесия, то ни один из игроков не извлечет для себя пользы, нарушив этот договор. Попытка зафиксировать в договоре неравновесную ситуацию приведет к тому, что хотя бы у одного из игроков окажутся стимулы нарушить этот договор с целью увеличения своего выигрыша.
Определение 2.3. Ситуация (х*,…, у*) называется ситуацией равновесия в чистых стратегиях, если для любых хЄх и уЄу выполнено двойное неравенство
H(x, y*)≤ H(x*, y*)≤ H(x, y*), (2.9)
где х*, у* — соответственно максиминная и минимаксная чистые стратегии игроков в случае v (Г) =  (Г) [14].
(Г) [14].
Обобщая, предположим, что игрок 1 в антагонистической игре Г= [X, Y, Н] выбирает некоторую свою стратегию x. Тогда в наихудшем случае (например, если выбор игроком 1 стратегии станет известным игроку 2), он получит выигрыш  . Предвидя такую возможность, игрок 1 должен выбрать свою стратегию x* таким образом, чтобы максимизировать этот свой минимальный выигрыш:
. Предвидя такую возможность, игрок 1 должен выбрать свою стратегию x* таким образом, чтобы максимизировать этот свой минимальный выигрыш:
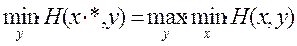 .
.
Стоящий в правой части неравенства «максимин» является, таким образом, гарантированным выигрышем игрока 1.
Теперь рассмотрим точку зрения игрока 2. Пусть он выбирает некоторую свою стратегию y. Тогда в наихудшем случае его проигрыш составит 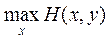 . Действуя с расчетом на наименее благоприятный ход событий, игрок 2 должен выбрать свою стратегию y* так, чтобы минимизировать свой максимальный проигрыш:
. Действуя с расчетом на наименее благоприятный ход событий, игрок 2 должен выбрать свою стратегию y* так, чтобы минимизировать свой максимальный проигрыш:
 .
.
Стоящий в правой части уравнения «минимакс» является максимальным неизбежным проигрышем игрока 2. Это означает, что, действуя достаточно разумно, игрок 2 не может не дать игроку 1 выиграть больше, чем этот минимакс.
Следовательно, если оба участника игры ведут себя разумно, то выигрыш игрока 1 должен быть не меньше, чем максимин
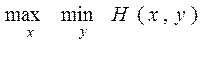
и не больше, чем минимакc
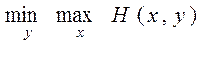 .
.
Если бы для какой-нить антагонистической игры оказалось, что минимакс  меньше максимина
меньше максимина  , то изложенное выше привело бы к противоречию и для подобной игры разумных поведений игроков не могло бы существовать. Однако, к счастью, максимин
, то изложенное выше привело бы к противоречию и для подобной игры разумных поведений игроков не могло бы существовать. Однако, к счастью, максимин  никогда не превышает минимакса
никогда не превышает минимакса  :
:
 .
.
B самом деле, при любых x и y
Н(x, y) 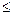 max H(x, y),
max H(x, y),
и тем более
 .
.
Так как это неравенство выполняется при любом х, оно
будет справедливо и для того x, которое обращает в максимум  :
:

Так как это неравенство в свою очередь имеет место при всяком y, то оно остается в силе и для такого y, которое обращает в минимум 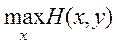 :
:

что и требовалось.
Если оба минимакcа равны:
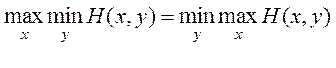 , (2.10)
, (2.10)
то выигрыш игрока 1 является вполне определенным числом. Игрок 1 всегда может себе обеспечить указанный выигрыш, а большей суммы ему не позволит выиграть противник. Этот точный выигрыш игрока 1 называется значением игры. Участие игрока 1 в игре означает получение им от игрока 2 именно этой суммы. Значение игры называется иногда ценой игры, так как его можно понимать, как ту справедливую цену, которую игрок 1 может заплатить за право участия в игре Г. Значение игры Г обычно обозначается через vT или просто v.
Итак, если имеет место равенство «минимаксов» (2.10), то разумные действия обоих участников игры приведут к тому, что игрок 1 выиграет (а игрок 2 соответственно проиграет) сумму, равную значению игры Г. Но, с другой стороны,разумные действия игроков должны приводить к ситуациям равновесия. В связи с этим естественно ожидать, в случае равенства минимаксов игроки, действуя указанным выше образом, отыскивают ситуацию равновесия, седловую точку [14].
Возвращаясь к содержательной терминологии, мы можем сказать, что оптимальная стратегия предприятия «Сокол» будет состоять в разработке программного продукта того же вида (направленности) (1 или 2), что и программный продукт, разрабатываемый предприятием «Чайка», а оптимальная стратегия на предприятии «Чайка» − выпускать БПО1. В этой связи фактически предприятие «Сокол» должно выпускать СПО1.
Практически, данный вывод можно было бы сделать и на основе рассуждений при рассмотрении табл. 1.2 или первичной табл. 1.1.
Таким образом, аппарат теории игр дает такие же результаты, которые получены путем логических рассуждений и не противоречит элементарной логике.
|
из
5.00
|
Обсуждение в статье: Антагонистическая игра с полной информацией |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

