 |
Главная |
Классические кооперативные игры
|
из
5.00
|
1. Природа и структура кооперативных игр n лиц. Пусть условия неантагонистического конфликта таковы, что допускается заключение взаимообязывающих соглашений о стратегиях, а выигрыши могут перераспределяться между игроками. Тогда достаточно рассматривать только суммарный выигрыш игроков, образующих коалицию, причем масштабы функций полезности игроков могут быть выбраны так, что полезности для любых двух игроков передаются без их численного изменения. В этом случае силу коалиции S полностью характеризует число  , которое определяется следующим образом.
, которое определяется следующим образом.
Объединение игроков из S означает превращение их в единого игрока 1, стратегией которого являются всевозможные совместные действия составляющих его игроков из S, а выигрышем – сумма выигрышей игроков  . В худшем случае для объединенного игрока 1 игроки из
. В худшем случае для объединенного игрока 1 игроки из  могут также объединяться в некоторого коллективного игрока 2 с интересами, диаметрально противоположными интересам игрока 1. В результате коалиция S (как игрок 1) может гарантировать выигрыш
могут также объединяться в некоторого коллективного игрока 2 с интересами, диаметрально противоположными интересам игрока 1. В результате коалиция S (как игрок 1) может гарантировать выигрыш  , равный значению возникающей антагонистической игры. Иными словами,
, равный значению возникающей антагонистической игры. Иными словами,  – гарантированное математическое ожидание выигрыша игроков коалиции S, действующих совместно против объединенных игроков коалиции
– гарантированное математическое ожидание выигрыша игроков коалиции S, действующих совместно против объединенных игроков коалиции  . Предположим, что значение
. Предположим, что значение  существует для любой коалиции
существует для любой коалиции  .
.
Определение 5.6: Кооперативной игрой n лиц называется пара  , где
, где  , а
, а  – функция, определенная на всех подмножествах
– функция, определенная на всех подмножествах  . Функция v называется характеристической функцией.
. Функция v называется характеристической функцией.
Таким образом, кооперативную игру n лиц можно анализировать с помощью характеристической функции, область определения которой состоит из 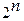 возможных подмножеств I. Если для всех непересекающихся подмножеств S и T (
возможных подмножеств I. Если для всех непересекающихся подмножеств S и T (  и
и  ) выполняется неравенство
) выполняется неравенство  , то характеристическая функция называется супераддитивной. Это свойство содержательно выражает то обстоятельство, что объединение игроков в коалиции является целесообразным с точки зрения увеличения выигрыша, т. е. данное условие отражает разумность коллективистской точки зрения. Далее будем рассматривать игры, для которых это условие выполняется.
, то характеристическая функция называется супераддитивной. Это свойство содержательно выражает то обстоятельство, что объединение игроков в коалиции является целесообразным с точки зрения увеличения выигрыша, т. е. данное условие отражает разумность коллективистской точки зрения. Далее будем рассматривать игры, для которых это условие выполняется.
Методом математической индукции из неравенства  нетрудно получить следующее неравенство:
нетрудно получить следующее неравенство:
 ,
,
где  – непересекающиеся коалиции. Следовательно,
– непересекающиеся коалиции. Следовательно,  .
.
В дальнейшем величина  будет обозначаться через
будет обозначаться через  .
.
Определение 5.7. Игра  называется существенной, если
называется существенной, если  . В противном случае игра
. В противном случае игра  называется несущественной.
называется несущественной.
Обозначим через  сумму, которую получит игрок
сумму, которую получит игрок  при распределении полезности, имеющейся в распоряжении множества игроков I, и дадим следующее определение.
при распределении полезности, имеющейся в распоряжении множества игроков I, и дадим следующее определение.
Определение 5.8: Дележом называется вектор  , удовлетворяющий условиям
, удовлетворяющий условиям
 для всех
для всех  ; (5.1)
; (5.1)
 (5.2)
(5.2)
Условие (5.1) называется условием индивидуальной рациональности и характеризует предположение, что, участвуя в коалиции, каждый игрок получает, по меньшей мере, столько, сколько он мог бы получить, действуя самостоятельно и не заботясь о согласии каких-либо других игроков. В противном случае он в распределении x будет получать меньше, чем  , и таким образом это распределение не будет реализовано. Вполне обосновано также условие (5.2), так как в случае
, и таким образом это распределение не будет реализовано. Вполне обосновано также условие (5.2), так как в случае  существует распределение
существует распределение 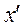 , при котором каждый игрок
, при котором каждый игрок 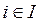 получит больше, чем его доля
получит больше, чем его доля  . Если же
. Если же  , то игроки из группы I делят между собой нереализуемую полезность, и поэтому вектор x неосуществим. Следовательно, вектор x может считаться допустимым только при выполнении условия (5.2), которое называется условием коллективной (или групповой) рациональности.
, то игроки из группы I делят между собой нереализуемую полезность, и поэтому вектор x неосуществим. Следовательно, вектор x может считаться допустимым только при выполнении условия (5.2), которое называется условием коллективной (или групповой) рациональности.
На основании условий (5.1), (5.2) для того чтобы вектор  был дележом в кооперативной игре
был дележом в кооперативной игре  , необходимо и достаточно выполнение равенства
, необходимо и достаточно выполнение равенства  ,
,  , причем
, причем  ,
, 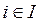 ,
,  .
.
Содержание понятия «делёж» можно трактовать как договор между игроками о распределении получаемой ими всеми суммы  .
.
В дальнейшем для любого дележа x через  мы будем обозначать величину
мы будем обозначать величину  , а множество всех дележей через H.
, а множество всех дележей через H.
Таким образом, исходом кооперативной игры является дележ, который производится в результате соглашений игроков. В связи с этим в кооперативных играх сравниваются по предпочтительности не ситуации, а дележи, и это сравнение, имея сложный характер, исходит из различных представлений об оптимальности для этих классов игр. В результате принципы оптимальности для кооперативных игр оказываются весьма разнообразными.
2. Доминирование дележей. Проблема анализа кооперативной игры состоит в том, чтобы определить дележ, который является результатом игры. Она тривиально разрешима для несущественной игры, так как в этом случае  и условия (5. 1), (5. 2) выполняются только при
и условия (5. 1), (5. 2) выполняются только при  . Следовательно, несущественная игра имеет единственный дележ
. Следовательно, несущественная игра имеет единственный дележ  .
.
Во всякой существенной игре с более чем одним игроком множество дележей бесконечно, поэтому будем анализировать такие игры при помощи отношения доминирования.
Пусть  и
и  – два дележа в кооперативной игре v, а
– два дележа в кооперативной игре v, а  – некоторая коалиция.
– некоторая коалиция.
Говорят, что дележ x доминирует над дележом y по коалиции S, если выполняются следующие два условия:
1) эффективность доминирующего дележа:  ;
;
2) предпочтительность:  для всех
для всех  .
.
Доминирование дележа y над дележом x по коалиции S обозначается через  .
.
Соотношение доминирования по коалиции S, т. е.  , выражает некоторое предпочтение, отдаваемое коалицией S дележу x по сравнению с дележом y. Оно призвано отображать то обстоятельство, что при выборе из двух дележей x и y коалиция S выберет x. Это можно понимать и так, что при предъявлении коалиции S дележа y как договора, коалиция S имеет основания выступить против y, предлагая в качестве альтернативы дележ x.
, выражает некоторое предпочтение, отдаваемое коалицией S дележу x по сравнению с дележом y. Оно призвано отображать то обстоятельство, что при выборе из двух дележей x и y коалиция S выберет x. Это можно понимать и так, что при предъявлении коалиции S дележа y как договора, коалиция S имеет основания выступить против y, предлагая в качестве альтернативы дележ x.
Фигурирующее в определении доминирования условие эффективности означает, что сравниваемый коалицией дележ x должен быть, прежде всего, реализуемым этой коалицией: сумма выигрышей каждого из членов коалиции не должна превосходить гарантированно получаемое ею количество. В противном случае коалиция, встретившись с дележом, дающим ей столько, сколько она самостоятельно не в состоянии получить, должна согласиться на него и не заниматься его сравниванием с какими-либо другими дележами.
Условие предпочтительности отражает необходимость «единодушия» в предпочтении со стороны коалиции: если хотя бы одно из неравенств будет нарушено, т. е. если хотя бы для одного из членов коалиции S выигрыш в условиях дележа y будет не меньшим, чем в условиях дележа x, то можно говорить о предпочтении дележа x дележу y. Это касается не всей коалиции S, а лишь теми ее членами, для которых соответствующее неравенство соблюдается.
Определение 5.9. Говорят, что дележ x доминирует дележ y, если существует такая коалиция S, для которой  .
.
Доминирование дележа y дележом x обозначается через 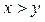 .
.
Доминирование дележа x над дележом y означает, что в «обществе» (т. е. во множестве всех участвующих в игре игроков I) найдутся такие «силы» (т. е. такая коалиция S), которые будут выступать в пользу дележа x по сравнению с дележом y.
Доминирование невозможно по одноэлементной коалиции и множеству всех игроков I. Действительно, из  следовало бы
следовало бы  , что противоречит условию (5.1).
, что противоречит условию (5.1).
А из  следовало бы
следовало бы  для всех
для всех  , и потому
, и потому  , что противоречит условию (5.2).
, что противоречит условию (5.2).
3. Эквивалентность кооперативных игр. Объединение кооперативных игр в те или иные классы существенно упрощает их последующее рассмотрение. В качестве таких классов можно взять классы эквивалентных игр.
Определение 5.10. Кооперативная игра  называется эквивалентной игре
называется эквивалентной игре  , если существует положительное число k и n таких произвольных вещественных чисел
, если существует положительное число k и n таких произвольных вещественных чисел  (
(  ), что для любой коалиции
), что для любой коалиции 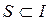 выполняется равенство
выполняется равенство
 (5.3)
(5.3)
Интересно сравнить это определение с определением стратегической эквивалентности бескоалиционных игр. В последнем случае было больше произвольных параметров. Это связано с тем, что в теории бескоалиционных игр полезности игроков могут иметь разные шкалы, а в кооперативных играх все игроки измеряют полезности в одной шкале.
Эквивалентность игры  и
и  будем обозначать как
будем обозначать как  ~
~  или
или 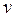 ~
~ 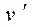 .
.
Очевидно, что v ~ v. Чтобы убедиться в этом, достаточно приравнять в формуле (5.3)  ,
, 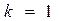 ,
,  . Только что доказанное свойство называется рефлексивностью. Докажем симметрию отношения, т. е. что из условия
. Только что доказанное свойство называется рефлексивностью. Докажем симметрию отношения, т. е. что из условия  ~
~  следует
следует  ~
~  . Действительно, полагая
. Действительно, полагая 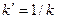 и
и  , получим
, получим  , т. е.
, т. е. 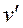 ~
~ 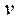 . Наконец, если
. Наконец, если  ~
~ 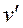 и
и  ~
~  , то
, то  ~
~  . Это свойство называется транзитивностью. Оно проверяется последовательным применением формулы (5.3). В силу того, что отношение эквивалентности рефлексивно, симметрично и транзитивно, оно разбивает множество всех игр на классы эквивалентных игр.
. Это свойство называется транзитивностью. Оно проверяется последовательным применением формулы (5.3). В силу того, что отношение эквивалентности рефлексивно, симметрично и транзитивно, оно разбивает множество всех игр на классы эквивалентных игр.
Теорема 5.2. Если две игры  и
и 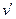 эквивалентны, то отображение
эквивалентны, то отображение  , где
, где  ,
,  , устанавливает такое взаимно однозначное отображение множества всех дележей игры v на множество дележей игры
, устанавливает такое взаимно однозначное отображение множества всех дележей игры v на множество дележей игры  , что из
, что из 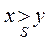 следует
следует  . Доказательство этой теоремы имеется в работе [9].
. Доказательство этой теоремы имеется в работе [9].
4. Нормализация игр (0–1-редуцированная форма). После разбиения множества кооперативных игр на попарно непересекающиеся классы эквивалентности возникает задача выбора по одному представителю от каждого класса. С этой целью дадим следующее определение и теорему.
Определение 5.11.Игра v называется игрой в 0–1-редуцированной форме, если  для всех
для всех  ,
,  .
.
Теорема 5.3. Каждая существенная кооперативная игра эквивалентна некоторой игре в 0–1-редуцированной форме. Доказательство этой теоремы имеется в работе [9].
5. С-ядро. Очевидно, что если игроки кооперативной игры  придут к такому соглашению о распределении выигрыша всей коалиции S (дележу
придут к такому соглашению о распределении выигрыша всей коалиции S (дележу  ), при котором ни один из дележей не доминирует над дележом
), при котором ни один из дележей не доминирует над дележом  , то такое распределение будет устойчивым (ни одной из коалиций S будет невыгодно отделиться от других игроков и распределять между членами S выигрыш
, то такое распределение будет устойчивым (ни одной из коалиций S будет невыгодно отделиться от других игроков и распределять между членами S выигрыш  ). Это замечание наводит на мысль о важности множества недоминируемых дележей.
). Это замечание наводит на мысль о важности множества недоминируемых дележей.
Определение 5.12: Множество недоминируемых дележей кооперативной игры называется ее С-ядром.
С-ядра кооперативной игры полностью описываются следующей теоремой.
Теорема 5.4. Для того чтобы дележ x принадлежал С-ядру, необходимо и достаточно выполнение неравенств  для любого
для любого  . Доказательство этой теоремы приводится в работе [9].
. Доказательство этой теоремы приводится в работе [9].
Из теоремы следует, что С-ядро является замкнутым выпуклым (возможно пустым) подмножеством множества всех дележей.
Очевидно, чем больше возможностей недоминирования в игре одних дележей над другими, тем выше вероятность наличия непустого С-ядра и тем большим может быть само С-ядро. «Наиболее благоприятным» в этом отношении представляется случай несущественной игры, в которой С-ядро существует и состоит из единственного дележа этой игры, а также случай игры двух лиц, в которой какое-либо доминирование отсутствует и С-ядро состоит из множества всех дележей.
6. Решение по Нейману – Моргенштерну (Н–М-решение). Было бы идеальным найти такое распределение выигрышей между игроками, которое находилось бы в С-ядре и доминировало бы над всеми остальными дележами. Однако это возможно только для несущественных игр, в которых множество дележей одноэлементно. Нейман и Моргенштерн предложили искать решения в виде подмножеств множества дележей, которые в некотором смысле выполняют роль рассматриваемого дележа, а именно элементы искомого подмножества должны доминировать над любыми дележами, лежащие вне его (внешняя устойчивость), и не доминировать друг над другом (внутренняя устойчивость). Формально это приводит к следующему определению.
Определение 5.13: Подмножество дележей R кооперативной игры  называется Н–М-решением, если
называется Н–М-решением, если
1) из  следует, что либо
следует, что либо  , либо
, либо  ;
;
2) для любого  существует такой
существует такой 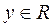 , что
, что 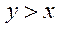 .
.
Прямые возможности применения понятия Н–М-решения на практике отсутствуют. Оно несет скорее философский, нежели практический смысл. Например, Н. Н. Воробьев интерпретирует понятие Н–М-решения как «представление о такой системе норм поведения, что последствия двух допустимых этими нормами поведений не могут быть противопоставлены какой-либо общественной силой (коалицией) друг другу, а каково бы ни было отклонение от допустимых поведений, в обществе (т. е. в множестве всех игроков I) найдутся такие силы (т. е. некоторая коалиция), которые будут стремиться к восстановлению нормы». Между С-ядром оперативной игры и ее Н–М-решением имеется известная связь. Например, если С-ядро непусто и существует Н–М-решение существует, то оно содержит С-ядро.
Теорема 5.5. Если для характеристической функции игры в 0–1-редуцированной форме  ,
,  выполняется неравенство
выполняется неравенство
 , где
, где 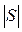 – число игроков в коалиции S, то С-ядро этой игры непусто и является ее Н–М-решением. (Доказательство этой теоремы имеется в работе[9].)
– число игроков в коалиции S, то С-ядро этой игры непусто и является ее Н–М-решением. (Доказательство этой теоремы имеется в работе[9].)
Понятие Н–М-решения при всей его естественности обладает также некоторыми недостатками. Отметим следующие из них.
Во-первых, известны примеры кооперативных игр, которые не имеют Н–М-решений. Более того, в настоящее время не известны какие-либо критерии, позволяющие судить о наличии в кооперативных играх Н–М-решений. Тем самым заложенный в Н–М-решении принцип оптимальности не является универсально реализуемым, и область его реализуемости остается пока неопределенной.
Во-вторых, кооперативные игры, если имеют Н–М-решения, то, как правило, более одного. В этой связи принцип оптимальности, приводящий к Н–М-решению, не является полным (указанный принцип, вообще говоря, не определяет единственную систему норм распределения выигрыша).
В-третьих, решения существенных кооперативных игр состоят более чем из одного дележа. Таким образом, даже выбор какого-либо конкретного Н–М-решения еще не определяет выигрыша каждого из игроков.
Наконец, в-четвертых, понятие Н–М-решения отражает лишь в весьма малой мере черты справедливости.
Перечисленные недостатки следует понимать не как пороки, которые следовало бы исправлять, а именно как недостатки, которые хотелось бы восполнить. К сожалению, такое восполнение рассматриваемого принципа оптимальности едва ли возможно, разве что за счет резкого сокращения области его реализуемости. Впрочем, это отражает существующее положение дел: большинство экономических и социальных проблем допускает множественные решения, и эти решения не всегда поддаются непосредственному сравнению в соответствии с их предпочтительностью.
7. Вектор Шепли. Ранее мы рассматривали решения (С-ядро, Н–М-решение), которые связаны с устойчивостью поведения игроков. Теперь остановимся на таких решениях, которые определяются некоторым третьим лицом – арбитром – согласно определенным понятиям «разумности» или «справедливости». С аналогичным подходом мы уже сталкивались при рассмотрении арбитражных схем. Теперь определим один из «справедливых» дележей.
Поставим в соответствие каждой кооперативной игре  вектор
вектор  , компоненты которого будем интерпретировать как полезности, получаемые игроками в результате соглашения или решения арбитра.
, компоненты которого будем интерпретировать как полезности, получаемые игроками в результате соглашения или решения арбитра.
Будем считать, что наши соображения о справедливом дележе воплощены в следующих четырех аксиомах 5.7-5.10, впервые несколько по-иному сформулированных Шепли в 1953 г.
Аксиома 5.7. Симметрия: пусть  – произвольная перестановка игроков, причем
– произвольная перестановка игроков, причем  . Тогда
. Тогда  , где через
, где через  обозначен образ игрока i при перестановке
обозначен образ игрока i при перестановке  .
.
Аксиома 5.8. Оптимальность по Парето:  .
.
Аксиома 5.9. Эффективность: если для любой коалиции  выполняется равенство
выполняется равенство  , то
, то  .
.
Аксиома 5.10. Агрегация: если характеристическая функция w игры  равна сумме характеристических функций v и u соответственно игр
равна сумме характеристических функций v и u соответственно игр 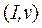 и
и  , т. е. для любой коалиции
, т. е. для любой коалиции  справедливо равенство
справедливо равенство  , то
, то  ,
,  .
.
Первые три аксиомы не вызывают возражений и, по-видимому, должны выполняться при любом определении «справедливого» дележа. Последняя аксиома не совсем естественна, так как предполагается, что при участии игроков в двух играх (сложение характеристических функций можно понимать как участие игроков I в двух играх) их выигрыши в отдельных играх должны складываться. В результате вектор  для некоторых игр приобретает ряд нежелательных свойств. Например, он не всегда содержится в С-ядре, даже когда оно непусто. Однако довольно часто дележ согласно вектору
для некоторых игр приобретает ряд нежелательных свойств. Например, он не всегда содержится в С-ядре, даже когда оно непусто. Однако довольно часто дележ согласно вектору  вполне удовлетворителен. Система состоящая из аксиом 1–4, является непротиворечивой и полной.
вполне удовлетворителен. Система состоящая из аксиом 1–4, является непротиворечивой и полной.
Определение 5.14: Пусть Ф – функция, ставящая в соответствие согласно аксиомам 1–4 каждой игре  вектор
вектор  . Тогда
. Тогда  называется вектором Шепли игры
называется вектором Шепли игры  .
.
Оказывается функция, для которой выполняются аксиомы 1–4, существует и единственна. Для каждой характеристической функции v вектор  является дележом.
является дележом.
Определение 5.15: Характеристическая функция  кооперативной игры называется простейшей, если она для любого T определяется равенством
кооперативной игры называется простейшей, если она для любого T определяется равенством
 .
.
Первые три аксиомы определяют вектор Шепли для простейших характеристических функций.
8. n-ядро. В 1969 г. Шмайдлер определил понятие n-ядра. По его мнению, распределение выигрыша  между игроками следует считать справедливым, если
между игроками следует считать справедливым, если  «мало» отличается от
«мало» отличается от 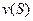 для любой коалиции
для любой коалиции  в том случае, когда
в том случае, когда  .
.
Величина  называется эксцессом.
называется эксцессом.
Эксцесс, по сути дела, есть разность между тем количеством 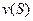 , на которое коалиция S может уверенно рассчитывать в условиях характеристической функции v, и тем количеством, которое на основе дележа x получат в сумме все участвовавшие в ней игроки. Таким образом, положительный эксцесс можно понимать, с одной стороны, как «запас» в реализуемости компонент дележа для игроков из S в условиях x, а с другой, как степень неудовлетворенности коалиции S дележом x в условиях v.
, на которое коалиция S может уверенно рассчитывать в условиях характеристической функции v, и тем количеством, которое на основе дележа x получат в сумме все участвовавшие в ней игроки. Таким образом, положительный эксцесс можно понимать, с одной стороны, как «запас» в реализуемости компонент дележа для игроков из S в условиях x, а с другой, как степень неудовлетворенности коалиции S дележом x в условиях v.
Эксцесс определен для любой непустой коалиции S. Набор из 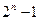 эксцессов является мерой близости дележа x и характеристической функции v: каждому дележу x ставится в соответствие
эксцессов является мерой близости дележа x и характеристической функции v: каждому дележу x ставится в соответствие 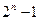 -мерный вектор
-мерный вектор
 ,
,  ,
,
где  – коалиция, для которой эксцесс максимален,
– коалиция, для которой эксцесс максимален,  – коалиция, имеющая следующий по величине эксцесс и т. д. Для вектора e выполняются неравенства
– коалиция, имеющая следующий по величине эксцесс и т. д. Для вектора e выполняются неравенства
 .
.
На множестве всех дележей введем следующее отношение предпочтения.
Пусть k – номер первой из координат вектора 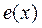 , которая отличается от соответствующей координаты вектора
, которая отличается от соответствующей координаты вектора  , т. е.
, т. е.  . Тогда
. Тогда  , если
, если  .
.
Максимальный элемент относительно предпочтения  называется n-ядром.
называется n-ядром.
Теорема 5.6. Для каждой кооперативной игры  существует единственное n-ядро. Доказательство этой теоремы имеется в работе [9].
существует единственное n-ядро. Доказательство этой теоремы имеется в работе [9].
Предположим теперь, что С-ядро кооперативной игры  не пусто. Если y не содержится, а x содержится в С-ядре, то очевидно,
не пусто. Если y не содержится, а x содержится в С-ядре, то очевидно,  , так как все координаты вектора
, так как все координаты вектора  неположительны, а вектор
неположительны, а вектор 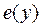 имеет, по крайней мере, одну положительную координату. В связи с этим n-ядро всегда содержится в С-ядре, если последнее непусто. В этом отношении n-ядро предпочтительнее вектора Шепли, который, вообще говоря, не содержится в С-ядре.
имеет, по крайней мере, одну положительную координату. В связи с этим n-ядро всегда содержится в С-ядре, если последнее непусто. В этом отношении n-ядро предпочтительнее вектора Шепли, который, вообще говоря, не содержится в С-ядре.
|
из
5.00
|
Обсуждение в статье: Классические кооперативные игры |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

