Антагонистическая игра без информации. Смешанные стратегии

Предположим, компании занимаются решением аналогичной задачи (рассмотренной в предыдущем разделе) с тем, однако, единственным отличием, что не только «Чайка» узнает о продукции предприятия «Сокол» после выбора ею своего вида программного продукта, но и «Сокол» не может получить предварительной информации и вынуждено принимать свое решение, не зная о решении предприятия «Чайка». Таким образом, в этом случае как «Чайка», так и «Сокол» имеют по одному информационному состоянию. В своем единственном информационном состоянии каждое из предприятий имеет две альтернативы: выпускать первый вариант своего программного продукта или второй его вариант. Эти альтернативы и будут стратегиями наших игроков.

Полученная игра является матричной, имеет 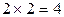ситуации, и матрицей выигрышей в ней, очевидно, будет:

	СПО1	СПО2
БПО1
БПО2

 

 

(2.11)

 

 

Согласно сказанному выше можно было бы в строках и столбцах не указывать их содержательного смысла. Все-таки сделаем это здесь для наглядности.

Строки матрицы, как и в предыдущем примере, выбирает игрок 1 –

«Чайка», а столбцы – игрок 2 «Сокол».

Матрица (2.11) является подматрицей матрицы (2.8). На рассмотренном примере видно, что ситуация равновесия предыдущей игры в матрицу (2.11) не попала, ибо весь второй столбец матрицы (2.8) в матрицу (2.11) не вошел. Никакой другой ситуации равновесия здесь не возникло, и максимин в матрице (2.11), равный 40, отличен от минимакса, который равен 70. Таким образом, максиминный принцип оптимальности в данном случае оказывается нереализуемым, по крайней мере, в той чистой форме, в какой он реализовался в игре из предыдущего раздела.

В итоге игрок 1 может уверенно получить 40 (максимин), но игрок 2 столь же уверенно не допустить, чтобы он получил более чем 70 (минимакс). Такое положение дел, естественно, порождает у игрока 1 мысли, что он, пожалуй, «исхитрившись», может получить уверенно несколько больше, чем 40 (пусть даже меньше, чем 70). Со своей стороны игрок 2 задумывается о том, как изловчиться и ограничить притязания игрока 1 не числом 70, а меньшим (хотя бы и большим, чем 40).

Одна из возможностей такого рода расширений состоит в том, чтобы разнообразить способы выбора своей стратегии. Например, стратегии можно выбрать случайно. Выбрать стратегию случайно – значит заранее вычислить вполне определенные вероятности, с которыми та или иная стратегия будет выбрана, реализовать некоторое случайное испытание, исходы которого имеют эти вероятности и, наконец, принять окончательно решение в соответствии с наблюдаемой реализацией.

Понятие вероятности естественно и с успехом применяется к массовым явлениям, которые происходят сами по себе или поддаются воспроизводству неограниченное или хотя бы достаточно большое число раз. При этом вероятность определяется отношением числа испытаний, при которых наше событие наступило, к общему числу испытаний. Так, подбрасывая монету несколько тысяч раз, можно убедиться в том, что частота (вероятность) выпадения герба близка к 1/2.

Однако отсюда никак не следует, что понятие вероятности и все связанные с ним рассуждения применимы только к массовым явлениям и неприменимы к явлениям единичным, однократным. Действительно, пусть нам предстоит бросить ту же монету один раз. Если эта монета достаточно симметрична, то и до того, как подбросить ее, можно оценить поровну шансы выпадения монеты лицевой и оборотной сторонами. Так как достоверному событию приписывается мера шансов (вероятность) «единица», а возможностью того, что упавшая монета останется стоять на ребре, можно пренебречь, вероятность падения монеты на каждую из ее сторон будет действительно равна 1/2.

Далее предположим, что два человека играют в орлянку. Если игроки поставили на различные стороны монеты, то монета подбрасывается и тот, кто ставил на выпавшую сторону монеты, забирает обе ставки (свою и противника). Такую игру можно считать справедливой и мотивировать свое отношение к ней тем, что игрок в данном случае может с одинаковыми вероятностями выиграть или проиграть. В дальнейшем будут допускаться вероятностные рассмотрения однократно осуществляемых явлений.

Переменная величина, значения которой зависят от исхода случайного испытания (например, от наступления или ненаступления случайного события), называется случайной величиной. Случайной величиной будет, например, выигрыш игрока 1 в игре, если он выбрал первую строку с некоторой вероятностью р, вторую – с вероятностью 1−р, а игрок 2 выбирает первый столбец (достоверно); этот выигрыш принимает значение 40 с вероятностью р и значение 70 с вероятностью 1−р. Положение игрока 1 можно при этом уподобить положению участника беспроигрышной лотереи, ожидающего выигрыш 40 с вероятностью р и выигрыш 70 с вероятностью 1−р. Естественно предположить, что само участие в такой лотерее представляет для игрока 1 некоторую ценность, зависящую от вероятности р и лежащую между 40 и 70. При этом если вероятность р близка к 1, т. е. шансы получить именно 40 весьма велики, то ценность участия в лотерее будет близка к 40, а если близка к нулю, то ценность участия в лотерее близка к 70. Для простоты здесь и далее будем принимать, что эта зависимость является линейной: ценность описанной лотереи измеряется величиной

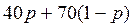. (2.12)

Будем называть эту величину ожидаемым выигрышем игрока 1 в рассматриваемых условиях.

Аналогично, если игрок 1 поступает, как в предыдущем случае, а игрок 2 выбирает второй столбец матрицы (2.11), то ожидаемый выигрыш игрока 1 будет равен

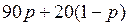. (2.13)

Предположим теперь, что игрок 2 по-прежнему выбирает первую строку с вероятностью р, а вторую с вероятностью 1−р, но игрок 2 также начал действовать наугад и выбирает первый столбец с вероятностью q, а второй с вероятностью 1−q. При этом предполагается, что вероятность q остается одной и той же. Выберет ли игрок 1 свою первую стратегию или вторую? В таких случаях в теории вероятностей (и в теории игр) принято говорить, что выборы игроков являются независимыми.

Такое положение дел можно уподобить участию игрока 1 в сложной лотерее, в которой с вероятностью q он получает билет на право участия в лотерее с ожидаемым выигрышем (2.12), а с вероятностью 1−q – в лотерее с ожидаемым выигрышем (2.13).

 

Далее можно сказать, что ожидаемый выигрыш игрока 1 будет равен

,

 

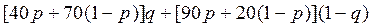или, раскрывая скобки и приводя подобные члены,

 

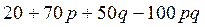. (2.14)

 

Будем теперь считать, что мы имеем дело с новой игрой, в которой участвуют те же игроки 1 и 2 (те же предприятия «Чайка» и «Сокол»). Стратегии игрока 1 состоят в выборе неотрицательного и не превосходящего единицы числа р, являющегося вероятностью выбора им первой строки матрицы; стратегии игрока 2 – в выборе вероятности q взятия им первого столбца, а значение функции выигрыша в ситуации, сложившейся в результате выбора вероятностей р и q, описывается выражением (2.14). Подчеркнем, что в этой игре каждый игрок имеет бесконечное множество стратегий. Ими будут любые числа в интервале от нуля и единицы.

Далее охарактеризуем смешанные стратегии. Итак, случайные, вероятностные стратегии игрока называются его смешанными стратегиями. Заметим, что при р = 1 или р = 0 стратегия игрока 1 будет состоять в достоверном выборе им первой или соответственно второй строки матрицы.

Таким образом, все старые стратегии входят в число новых, смешанных. Чтобы выделить их особое положение среди всех смешанных стратегий игрока 1, их обычно называют его чистыми стратегиями. Точно так же вводятся смешанные стратегии игрока 2 и среди них выделяются его чистые стратегии.

Смешанную стратегию игрока, состоящую в выборе его первой чистой стратегии с вероятностью t, а второй чистой стратегии с вероятностью 1−t, принято обозначать в виде пары чисел (t, 1−t).

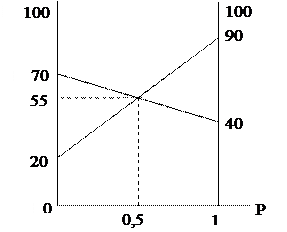
Рис. 2.1

Сначала найдем максимин выражения (2.14), т. е. максимальное значение минимального выигрыша игрока 1, которое он соответствующим выбором р может себе обеспечить. Представим для этого выражение (2.14) в виде

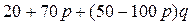. (2.15)

Если р ≤ 0,5, то коэффициент в выражении (2.15) при q неотрицателен, и, следовательно, игрок 2 для уменьшения выигрыша своего противника может взять наименьшее значение q, т. е. 0. Тогда выигрыш 1 будет равен 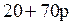. Но для максимизации этого выражения игроку 1 будет выгодно взять наибольшее р, допускаемое в этой области, т. е. 0,5. Его выигрыш при этом окажется равным .

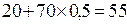Если р ≥ 0,5, то коэффициент в выражении (2.15) при q не положителен и игроку 2 будет выгодно взять значение q = 1. Выигрыш 1 составит 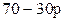, и для игрока 1 будет целесообразно взять наименьшее значение из р, для которого р ≥ 0,5, т. е. само число 0,5, получив при этом ожидаемый выигрыш 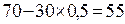. В обоих случаях максимальные выигрыши игрока оказались равными, чего, впрочем, и следовало ожидать, так как наибольшие значения достигаются здесь при одном и том же значении р, именно при р = 0,5 .

Все изложенные рассуждения иллюстрируются графическими построениями (рис. 2.1).

Итак, выяснилось, что значение максимина равно 55 и достигается он при смешанной стратегии (1/2, 1/2) игрока 1.

Далее следует найти минимакс. Представив выражение (2.14) в виде 20 + 50 q + (70 – 100 q) p , заметим, что в случае q ≤ 0,7 максимум достигается при р = 1 и равен 20 + 50 q + 70 – 100 q = 90 – 50 q, а если q ≥ 0,7, то максимум достигается при р = 0 и равен 20 + 50 q. Поэтому для игрока 2 будет целесообразно взять q = 0,7, т. е. смешанную стратегию (7/10, 3/10), и минимакс окажется равным .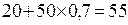

Следовательно, смешанные стратегии (1/2, 1/2) игрока 1 и (7/10, 3/10) игрока 2 являются их оптимальными стратегиями или, что то же самое, представляют собой ситуацию равновесия. Число 55 является значением игры.

В антагонистической игре оптимальная стратегия игрока является как бы стратегией, «пугающей» противника, вынуждающей его действовать также оптимально. Например, если бы в рассматриваемой игре игрок 1 применил бы вместо найденной оптимальной стратегии другую, скажем, стратегию (1/5, 4/5), то игрок 2 смог бы, выбрав свою вторую чистую стратегию, дать игроку 1 выиграть только 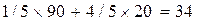, т. е. меньше, чем значение игры.

Обобщая, предположим, что игрок 1 в антагонистической игре Г=[X, Y, Н] выбирает некоторую стратегию x. Тогда в наихудшем случае (например, если выбор игроком 1 стратегии станет известным игроку 2), он получит выигрыш

.

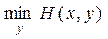Предвидя такую возможность, игрок 1 должен выбрать свою стратегию x* таким образом, чтобы максимизировать свой минимальный выигрыш:

.

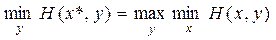Стоящий в правой части написанного равенства «максимин» является, таким образом, гарантированным выигрышем игрока 1.

Посмотрим теперь на эту игру с точки зрения игрока 2. Пусть он выбирает некоторую стратегию y. Тогда в наихудшем случае его проигрыш составит .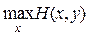

Действуя с расчетом на наименее благоприятный для себя ход событий, игрок 2 должен выбрать свою стратегию y* так, чтобы минимизировать максимальный проигрыш:

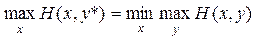. (2.16)

«Минимакс» в правой части равенства является максимальным неизбежным проигрышем игрока 2. Это означает, что, действуя, руководствуясь здравым смыслом, игрок 2 не может не дать игроку 1 выиграть больше указанного минимакса.

Следовательно, если оба участника игры ведут себя разумно, то выигрыш игрока 1 должен быть не меньше, чем максимин ,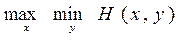

и не больше, чем минимакc

.

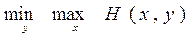Если бы для какой-нить антагонистической игры оказалось, что минимакс

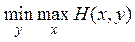
меньше максимина

 

,

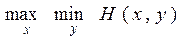то изложенные выше рассуждения привели бы нас к противоречию и для такой игры разумного поведения игроков не могло бы существовать. Однако, к счастью, максимин

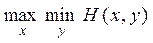
никогда не превышает минимакса

:

.

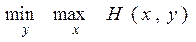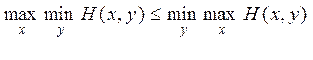B самом деле, при любых x и y

Н(x, y) 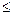max H(x, y) , (2.17)

и, тем более,

.

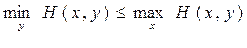Так как это неравенство выполняется при любом х, оно
будет справедливо и для того x, которое обращает в максимум :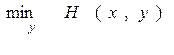

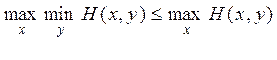
Так как это неравенство в свою очередь справедливо при любом у, то оно верно и для такого y, кото­рое обращает в минимум :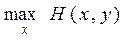

,

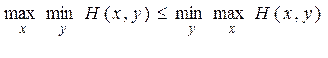что и требовалось.

Если оба минимакcа равны:

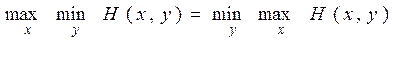, (2.18)

то выигрыш игрока 1 является вполне определенным чис­лом. Игрок 1 может всегда обеспе­чить себе этот выигрыш, а большей суммы ему не позволит выиграть про­тивник. Точный выигрыш игрока 1 называется зна­чением игры. Участие игрока в игре означает получение им от игрока 2 именно этой суммы. Значение игры назы­вается иногда ценой игры, так как ее можно понимать, как ту справедливую цену, которую игрок 1 может запла­тить за право участия в игре Г. Значение игры Г обычно обозначается через v_T или просто v.

Итак, если имеет место равенство «минимаксов» (2.18), то разумные действия обоих участников игры приведут к тому, что игрок 1 выиграет (а игрок 2 соответственно проиграет) сумму, равную значению игры Г. Но, с другой стороны,разумные действия игроков должны приводить к ситуациям равновесия, поэтому естественно ожидать что, в случае равенства минимаксов игроки, действуя указанным выше образом, осуществляют ситуацию равновесия, определяют седловую точку [14].

Сформулируем полученный вывод в содержательных терминах. Оптимальной стратегией предприятия «Чайка» является выпуск БПО первого и второго видов с вероятностями 0,5 каждая. Оптимальной стратегией предприятия «Сокол» является выпуск СПО₁ с вероятностью 0,7 и СПО₂ с вероятностью 0,3. Ожидаемая реализация программных продуктов, произведенных предприятием «Чайка», составляет 55 %, а произведенных предприятием «Сокол» − 45 %.

Очевидно, что наличие информации о планах предприятия «Чайка» (случай игры с информацией) позволяет предприятию «Сокол» вместо 45 % продукции сбыть 60 %. Вопрос о том, дорогая это плата за информацию или нет, уже выходит за рамки данной задачи, равно как и за пределы теории игр вообще.

Многошаговые игры

Основы теории

Рассмотрим многоходовую игру, например, шахматы или «крестики-нолики». Предположим, что, играя в «крестики-нолики», необходимо сосчитать число стратегий первого игрока. Заметим (пренебрегая симметрией), что при первом ходе игрок имеет девять альтернатив. Далее для любого из восьми возможных ответов на втором ходе у него будет семь альтернатив. Если рассмотреть только первые два хода первого игрока, то выяснится, что у него 9·7⁸=51 883 209 чистых стратегий. Естественно, что возможность перечислить их весьма сомнительна.

Вспомним определение чистой стратегии: это функция, определенная на совокупности информационных множеств одного игрока и приписывающая каждому информационному множеству число между 1 и k (где k – число альтернатив в данном информационном множестве). Таким образом, если у игрока N информационных множеств и в каждом из них k альтернатив, то общее число чистых стратегий равно k^N, а это число может быть очень большим. Если вернуться к примеру с «крестиками-ноликами», станет ясно, что никто не играет в эту игру, рассматривая все возможные чистые стратегии (т. е. все возможные последовательности ходов с первого до последнего). Скорее, в нее играют, рассматривая на каждом ходе все возможные альтернативы только для этого хода и выбирая из них наилучшую (исходя из собственного опыта или как-либо иначе). Итак, здесь сущность упрощения состоит в том, чтобы рассматривать ходы по одному за раз. Этот прием сводит один выбор из

k₁ k₂…k_N возможных стратегий к N выборам из k_i возможных альтернатив в каждом информационном множестве. Отсюда следует определение: стратегией поведения называется набор N вероятностных распределений, каждое из которых задано на множестве возможных альтернатив в каждом информационном множестве.

Определение 3.1. Деревом игры (древовидно упорядоченным множеством) называется конечное множество К, частично упорядоченное отношением <, в котором:

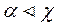а) каковы бы ни были , из условий и 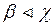следует, что либо 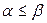, либо 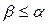(условие предпочтения сверху);

б) существует такое 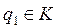, что 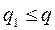для любого .

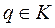Элементы древовидного упорядоченного множества называются позициями. В каждой позиции делает ход один из игроков.

Дерево игры изображается графически с помощью диаграммы, состоящей из конечного числа вершин (рис. 3.1). Вершины являются позициями, а ребра соединяют позиции, непосредственно следующие друг за другом. Ребра, соединяющие некоторую позицию с непосредственно следующей за ней, называются альтернативами этой позиции. Альтернативы каждой позиции нумеруются натуральными числами. Если позици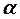и и 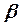находятся в отношении 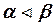, то позицию 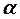называют предыдущей, а позицию 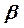– последующей. Позиции, не имеющие последующих, называются окончательными, а остальные – неокончательными. Множество окончательных и неокончательных позиций будем обозначать соответственно через Т и Q. Очевидно, что 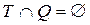и .

 

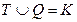Построение диаграммы (рис. 3.1) игры начинается с начальной позиции, где указывается, какой из игроков делает ход. Из вершины 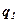проводятся ребра, соответствующие альтернативам игрока, который делает первый ход. Они соединяют вершину 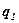с вершинами (позициями) игроков, которые делают следующий ход, и так далее, до тех пор, пока не будут обозначены окончательные вершины. На диаграмме рядом с каждой вершиной указывается игрок, который делает ход.

Каждая окончательная вершина определяет единственную цепь – последовательность идущих друг за другом дуг, ведущую от начальной вершины к данной. Эта цепь является партией игры. Число различных партий равно числу окончательных вершин. На множестве окончательных вершин определена функция М(t), которая указывает, сколько выигрывает первый игрок, если игра закончится в вершине .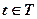

 

Разбиение множества Q на подмножества, учитывающие ходы игроков, устанавливает чередование ходов. В связи с этим множества Q_i называются множествами очередности, т. е. в позиции 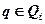очередность хода принадлежит игроку i.

 

Каждое из множеств очередности разбивается на попарно не пересекающиеся информационные множества. При этом все позиции из одного информационного множества должны иметь одно и то же число альтернатив, и никакая позиция не должна следовать за другой позицией, принадлежащем тому самому информационному множеству.

 

Содержательный смысл информационного множества состоит в том, что игрок в каждый момент игры знает, в каком информационном множестве он находится, но не знает, в какой именно позиции рассматриваемого множества.

 

Очевидно, что если информационное множество состоит из одной позиции, то игроку известно, как протекала партия до этого момента, поэтому говорят, что игрок имеет полную информацию в игре, если каждое его информационное множество состоит из одного элемента. Семейство всех информационных множеств игрока i (i=0, 1, 2) будем обозначать через U_i, принимая, что каждое множество U₀ одноэлементно.

 

Следовательно, динамика конфликта отражается в игре посредством множеств очередности, а информативность игроков определяется семействами информационных множеств.

Определение 3.2.Позиционной структурой С называется следующая система:

а) ориентированное дерево позиции К с начальной позицией (дерево отражает структуру ходов, т. е. связь каждого хода со всеми другими ходами, а начальная позиция – первый ход игры);

б) разбиение множества Q=K/T всех неокончательных позиций на множества очередности Q₀, Q₁, Q₂ (для каждого хода указывается, какой из игроков его делает);

в) подразбиение множеств очередности Q₁ и Q₂ на информационные множества U₁ и U₂ (подразбиение отражает информацию игрока i (i=1, 2) для каждого его хода на дереве игры);

г) вероятностные распределения на множествах альтернатив каждой позиции q из U₀;

д) нумерация альтернатив каждой позиции из одного информационного множества одними и теми же числами 1, 2, …, k (каждое число определяет по одной альтернативе в каждой позиции данного информационного множества).

Процесс игры с позиционной структурой С определяется следующим образом. Первый ход состоит в выборе альтернатив в начальной позиции q_1. Пусть n ходов уже произведены, в результате чего получена позиция 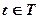. Тогда процесс считается законченным, а игрок i (i=1, 2) получает выигрыш M_i(t). Если позиция 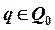, то игра переводится из позиции q в одну из последующих позиций, которая определяется согласно распределению вероятностей на множестве альтернатив позиции q.

 

Если ж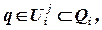е где 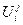- j-е информационное множество игрока i, i=1,…, s; s – число информационных множеств игрока i, то игрок i, зная, что находится в одной из позиций информационного множества 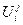, выбирает произвольно одну из альтернатив, и тем самым игра приходит в позицию g и т. д.

Определение 3.3. Чистой стратегией игрока будем называть заранее определенную последовательность ходов игрока в зависимости от информации о ходах другого игрока и ходах игрока 0 (природы).

 

Так, чистая стратегия, будучи планом проведения игры со структурой С данным игроком, предопределяет выбор одной из альтернатив, имеющихся в его распоряжении на каждом очередном ходе.

Формально чистой стратегией игрока i в игре со структурой С называется функция, определенная на U_i , значениями которой являются альтернативы информационных множеств.

Если игрок имеет r информационных множеств, причем любая позиция l-го (l=1, 2,…, r) множества обладает k_l альтернативами, то общее число чистых стратегий игрока равно

(3.1)

Определение 3.4. Будем говорить, что задана антагонистическая конечная позиционная игра Г, если заданы:

а) позиционная структура С;

б) принимающая вещественные значения функция выигрыша M(t), определенная на множестве всех окончательных позиций дерева структуры С.

В том случае, если в игре не участвует игрок 0 (природа, случай), выбор первым игроком чистой стратегии x, а вторым игроком – чистой стратегии y однозначно определяет исход игры, т. е. упорядоченная пара τ = (x, y) приводит к i-й окончательной вершине и первый игрок получает выигрыш M(t). Если в игре участвует игрок 0 (природа, случай), то пара τ определяет распределение вероятностей на множестве

T={t₁, t₂,…, t_s} окончательных вершин

 

P(τ, t) ≥ 0, 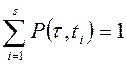, (3.2)

где P (τ, t) – вероятность того, что партия закончится в вершине .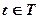

Распределение вероятностей P (τ, t) естественным образом приводит к математическому ожиданию выигрыша первого игрока, которое определяется следующим образом:

 

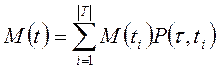, (3.3)

где 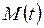- выигрыш первого игрока в окончательной позиции t_i , а |T| - число окончательных позиций.

На основе изложенного выше можно придти к заключению, что каждая пара чистых стратегий игроков 1 и 2 приводит к некоторой ситуации, в которой первый игрок получает определенный выигрыш или математическое ожидание выигрыша. На множестве пар чистых стратегий задана функция H, которая указывает выигрыш или математическое ожидание выигрыша первого игрока, если игроки будут применять данные чистые стратегии. Это функция выигрыша игрока 1 [9].