 |
Главная |
Решение биматричной игры
|
из
5.00
|
| Стратегии предприятия «Сокол» Стратегии предприятия «Чайка» | БПО1→ СПО1 БПО2→ СПО1 | БПО1→ СПО1 БПО2→ СПО2 | БПО1→ СПО2 БПО2→ СПО1 | БПО1→ СПО2 БПО2→ СПО2 |
| БПО1 | БПО1→ СПО1 40:60 | БПО1→ СПО1 40:60 | БПО1→ СПО2 90:10 | БПО1→ СПО2 90:10 |
| БПО2 | БПО2→ СПО1 70:30 | БПО2→ СПО2 20:80 | БПО2→ СПО2 70:30 | БПО2→ СПО2 20:80 |
Предположим теперь, что условия разработки систем на предприятиях «Чайка» и «Сокол» остались прежними, но конъюнктура на рынке изменилась и возможности сбыта возросли следующим образом. Согласно исследованиям маркетологов, просматривается тенденция внедрения системы в комплексе (СПО и БПО). Можно предполагать, что из тысячи рассматриваемых покупателей в случае появления на рынке СПО и БПО 50 % приобретут обе эти системы, а остальной спрос распределится согласно данным табл. 1.2: будет продано 400 и 100. Склонности к приобретению комплексов СПО и БПО другого вида маркетологи, однако, не обнаружили.
Подобное положение дел также описывается игрой двух игроков с двумя стратегиями у каждого, что и в рассматриваемой выше игре. Однако эта игра уже не будет антагонистической: от разработки систем выигрывают оба предприятия. Например, в ситуации (СПО1, БПО1) (600 шт., 900 шт.).
Общая сумма проданных систем будет зависеть теперь от складывающейся ситуации, поэтому будем измерять выигрыши игроков не в процентах, а абсолютно, в штуках. Выигрыши игрока 1 (предприятие «Чайка») могут быть описаны следующей матрицей
 (4.3)
(4.3)
Поскольку игра не является антагонистической и сумма выигрышей в каждой ситуации неодинакова, задание матрицы выигрышей игрока 1 еще не определяет матрицы выигрышей игрока 2. Последняя имеет в нашем случае вид

Ввиду того что выигрыши в неантагонистических играх двух игроков с конечным числом стратегий у каждого описываются парами матриц, такие игры принято называть биматричными.
Для предприятия «Заря» в условиях использования смешанных стратегий максиминная стратегия (ориентация исключительно на собственный выигрыш, описываемый матрицей (4.3)), находится, как и в примере из предыдущего раздела. Соответствующие расчеты показывают, что игрок 1 должен при этом выбирать свои строки матрицы с вероятностями (1/6, 5/6); при этом он должен опасаться смешанной стратегии (1/2, 1/2) игрока 2. Но, с другой стороны, из матрицы следует, что максиминной смешанной стратегией игрока 2 является (8/11, 3/11), а вовсе не пугающая игрока 1 стратегия (6/11, 5/11). Причем, сам он должен опасаться стратегии (6/11, 5/11) игрока 1 (а не играемой им стратегии (1/6, 5/6), которую в силу проведенных рассуждений склонен применять игрок 1).
Таким образом, в случае неантагонистической игры использование игроками в качестве оптимальных их максиминных стратегий неубедительно. Однако другая черта оптимальных стратегий антагонистических игр, именно их равновесность, оказывается более глубокой и «выдерживает» обобщение и на неантагонистические и в том числе на биматричные игры.
Найдем ситуации равновесия в нашем случае. Непосредственная проверка дала основания полагать, что ситуаций равновесия, в которых оба игрока имеют чистые стратегии, в рассматриваемой игре нет. Например, от ситуации, состоящей в выборе игроками своих первых чистых стратегий (соответствующие выигрыши расположены в левом верхнем углу матриц), выгодно отклониться игроку 1. Аналогично проверяется неравновесность остальных трех ситуаций в чистых стратегиях.
Следовательно, в ситуациях равновесия рассматриваемой игры хотя бы один игрок имеет смешанную стратегию, не являющуюся чистой, т. е. в которой вероятности обеих чистых стратегий отличны от нуля (такие смешанные стратегии принято называть вполне смешанными). Пусть для определенности это будет игрок 1, а его равновесная стратегия есть (р, 1—p), где 0 < р < 1. Подчеркнем, что число р нам пока неизвестно. Равновесной стратегией игрока 2 пусть является (q, 1 — q)', вообще говоря, она может быть и чистой, т. е. 0 ≤ q ≤ 1.
Тогда ожидаемый выигрыш игрока 1 в ситуации, сложившийся в результате применения этих двух стратегий, равен
400 рq+ 900р (1 — q) + 700 (1 — р) q + 600 (1 — р) (1 — q).
Обозначим этот выигрыш через Н (р, q). После упрощений получаем
H(р, q) = 600 + 300р + 100q —600pq
По определению ситуации равновесия, если игрок 1 изменит свою стратегию (р, 1—p) на какую-либо иную, то его выигрыш может только уменьшиться. В частности, такое уменьшение будет иметь место, если он заменит стратегию (р, 1—p) на свою первую или вторую чистые стратегии, т. е. на стратегии, в которых  или
или  . Это означает, что
. Это означает, что
 (4.4)
(4.4)
 (4.5)
(4.5)
Умножим неравенство (4.4) почленно на положительное число р, неравенство (4.5) ‑ на положительное 1—p и сложим полученные неравенства. Мы получим 
 , т. е. фактически точное равенство. Но точное равенство может получиться в результате сложения двух неравенств одинакового смысла только в том случае, когда оба они суть равенства. Далее, складываемые равенства отличаются, от соотношений (4.4) и (4.5) только положительными множителями р и 1—p. Следовательно, и эти соотношения должны быть равенствами, а так как две величины, порознь равные третьей, равны между собой, получаем
, т. е. фактически точное равенство. Но точное равенство может получиться в результате сложения двух неравенств одинакового смысла только в том случае, когда оба они суть равенства. Далее, складываемые равенства отличаются, от соотношений (4.4) и (4.5) только положительными множителями р и 1—p. Следовательно, и эти соотношения должны быть равенствами, а так как две величины, порознь равные третьей, равны между собой, получаем  , откуда q = 1/2. Следовательно, равновесная стратегия игрока 2 должна быть также вполне смешанной, именно (1/2, 1/2).
, откуда q = 1/2. Следовательно, равновесная стратегия игрока 2 должна быть также вполне смешанной, именно (1/2, 1/2).
Для нахождения числа р обратимся к выигрышу игрока 2 в ситуации равновесия. Он равен  .
.
Преобразование этого выражения и БПО2, сравнение его с выигрышем игрока 2 при выборе этим игроком его чистых стратегий дает подобно предыдущему, р = 6/11. Следовательно, равновесной стратегией игрока 1 оказывается (6/11, 5/11), что согласуется с предположением о ее смешанности.
Таким образом, рассматриваемая игра имеет только одну ситуацию равновесия, которая состоит из стратегии (6/11, 5/11) игрока 1 и стратегии (1/2, 1/2) игрока 2.
Как легко подсчитать по формулам (4.4) и (4.5), ожидаемые выигрыши игроков 1 и 2 в этой ситуации равновесия соответственно равны 650 и 464.
Сформулируем полученные выводы в содержательных терминах. В условиях рассматриваемой неантагонистической игры для предприятия «Чайка» представляется разумным выпуск программного обеспечения для ведения бухгалтерского учета первого вида с вероятностью 6/11, программного обеспечения для ведения бухгалтерского учета второго вида ‑ с вероятностью 5/11; для предприятия «Сокол» целесообразно производство программного обеспечения для управления складскими запасами первого вида и программного обеспечения для управления складскими запасами второго вида с одинаковыми вероятностями. Ожидаемая реализация продукции составляет для предприятия «Чайка» 650 шт., а для предприятия «Сокол» – 464 шт. Общее ожидаемое число реализованных программ составит 1114 шт.
Найденное разрешение конфликта является единственно оптимальным с точки зрения равновесия. Однако рассматриваемый вариант игры является неантагонистическим, и потому некоторые ситуации могут оказаться более выгодными и для обоих игроков, чем другие и, в частности, чем только что найденная ситуация равновесия.
Легко проверить, что самой выгодной ситуацией в рассматриваемой является та, в которой оба игрока применяют свои вторые чистые стратегии. В данном случае суммарный выигрыш игроков равен 1500 и представляется игроку 1 целесообразным (чтобы игроки договорились играть именно эти свои стратегии).
Но здесь возникают сразу две новые проблемы. Во-первых, получение игроком 1 выигрыша 600, а игроком 2 выигрыша 900, причитающихся им в наиболее выгодной ситуации, может стать причиной несогласия игрока 1, который, играя свою равновесную стратегию, мог бы получить 650. Он с полным основанием будет считать, что договор, условием которого является выбор игроками вторых стратегий, выгоден лишь для игрока 2 и невыгоден для него самого.
Кроме того, так как в этом договоре зафиксирована неравновесная ситуация, для одной из договаривающихся сторон будет выгодно его нарушить. В данном случае нарушение будет выгодно для «обиженного» игрока 1. Он может в последний момент отклониться от условий договора и выбрать свою первую чистую стратегию. В результате он резко увеличит свой выигрыш (до 900), оставляя противнику лишь 100. Следовательно, необходимо сделать так, чтобы игрок 1 был заинтересован в соблюдении условий договора.
Но игрок 1, соблюдая договор, обязывающий его выпускать БПО2, сможет согласно правилам игры (т. е. в рассматриваемой интерпретации – непосредственно от продажи программных продуктов) получить лишь 600. В связи с этим его заинтересованность в данной ситуации может быть удовлетворена лишь за счет игрока 2, получающего весьма много, 900. Очевидно, в договор следует включить пункт о компенсации игроком 2 игроку 1 убытков вследствие соблюдения договора. Для того чтобы не вызывать здесь возможных юридических возражений по поводу такого рода компенсаций, подчеркнем, что выигрыши игроков мы можем измерять не в деньгах, а в весьма широко понимаемых «единицах полезности».
Здесь, однако, мы сталкиваемся со второй проблемой. Какую по величине компенсацию со стороны игрока 2 игроку 1 можно считать «справедливой»?
Игрок 2 готов предложить разделить весь суммарный выигрыш 1500 пополам, т. е. так, чтобы каждый из участников игры получил по 750. Игрок 1, однако, не согласен и на это, мотивируя свое несогласие тем, что сам переход от антагонистической игры к неантагонистической, рассматриваемой нами в настоящий момент, связан с увеличением выигрыша игрока 1 на 400 единиц, а игрока 2 лишь на 100. В связи с этим игрок 1 считает себя вправе претендовать на долю, большую, чем половина от суммарного выигрыша. Он может иметь следующее представление о справедливости в данных условиях. Свой выигрыш в единственной ситуации равновесия каждый игрок может обеспечить себе, действуя в одиночку, поэтому деление общего выигрыша следует начать с выдачи равновесных выигрышей игрокам. По отношению к оставшейся сумме игроки находятся в одинаковом положении, ее следует разделить между ними пополам. В результате игрок 1 должен получить 843, а игрок 2 – 657.
КООПЕРАТИВНЫЕ ИГРЫ
Основы теории
Кооперативная игра задается множеством игроков N = {1, …, n} и характеристической функцией ν: 2N→ R, ставящей в соответствие каждой коалиции игроков S  N ее выигрыш.
N ее выигрыш.
Определение 5.1. Дележом игры (N, ν) называется вектор x = (x1, …, xn), для которого
 (свойство эффективности),
(свойство эффективности),

 (свойство индивидуальной рациональности).
(свойство индивидуальной рациональности).
Решением кооперативной игры обычно считается множество дележей, которые реализуемы при рациональном поведении игроков. Различные концепции решения кооперативных игр отличаются предположениями о рациональном поведении игроков.
Говорят, что дележ x доминирует над дележом y по коалиции S (  ), если
), если 
 >
>  ,
,  .
.
Если существует такая коалиция S, что  , говорят, что дележ x доминирует над дележом y. Множество недоминируемых дележей игры называется ее C-ядром.
, говорят, что дележ x доминирует над дележом y. Множество недоминируемых дележей игры называется ее C-ядром.
Определение 5.2.Для заданного множества игроков N сбалансированным покрытием называется такое отображение  множества собственных коалиций 2N\{N} на отрезок [0, 1], что
множества собственных коалиций 2N\{N} на отрезок [0, 1], что  для всех игроков
для всех игроков  (суммирование ведется по собственным коалициям, содержащим игрока i).
(суммирование ведется по собственным коалициям, содержащим игрока i).
Необходимые и достаточные условия непустоты С-ядра определяются согласно теореме О.Н. Бондаревой: С-ядро игры (N, ν) непусто тогда и только тогда, когда для любого сбалансированного покрытия 

Определение 5.3.Игры с непустым C-ядром (см. разд. 5.3.5) называются сбалансированными.
Определение 5.4.Кооперативная игра называется несущественной, если для произвольной коалиции 
 , в противном случае игра называется существенной.
, в противном случае игра называется существенной.
Несущественность игры означает нулевой эффект от кооперации игроков. Игровая ситуация является сильным равновесием Нэша, если никакая коалиция не может выиграть, отклоняясь от равновесной ситуации. Множество сильных равновесий Нэша может оказаться пустым, однако если в некоторой игре с трансферабельной полезностью игроков имеется единственное сильное равновесие Нэша, то соответствующая кооперативная игра будет несущественной. Концепция решений в угрозах и контругрозах основана на следующей идее. Пусть, например, в процессе игры трех лиц образовалась коалиционная структура {{1, 2}, {3}}, содержащая коалицию T = {1, 2}, в которую входят игроки с номерами 1 и 2. При распределении дохода коалиции ν({1, 2}) игроки 1 и 2 получают суммы x1 и x2 соответственно. Тогда, если игрок 1 недоволен таким распределением, он может предупредить своего партнера, что, если его доля дохода не будет увеличена, то он сформирует коалицию S = {1, 3}, где сможет рассчитывать на больший выигрыш. Если такая коалиция S может образоваться, т.е. если игроку 3 выгодно сменить конфигурацию x на новую конфигурацию y, то такое заявление называется угрозой игрока 1 игроку 2. В свою очередь, игрок 2 может заявить игроку 1, что в случае подобных его действий он может предложить игроку 3 такую конфигурацию z коалиционной структуры {{1}, {2, 3}}, что игрок 3 получит больший доход, чем в конфигурации y, а сам игрок 2 получит не меньше, чем в исходной конфигурации x. Таким образом, игрок 2 выдвигает контругрозу, «защищающую» его долю x2. Тогда распределение выигрыша коалиций некоторой коалиционной структуры между своими участниками является равновесием в угрозах и контругрозах, если на каждую угрозу произвольной коалиции K против любой другой коалиции L найдется контругроза коалиции L против коалиции K.
Арбитражные схемы
1. Природа и структура арбитражных схем. Большинство неантагонистических конфликтов в экономике и смежных с ней областях характеризуются тем, что их участники могут путем кооперирования объединять свои усилия. Сотрудничество между игроками приводит к качественно новому конфликту по сравнению с бескоалиционным вариантом.
В бескоалиционных играх отклонение одного из участников от ситуации равновесия не дает ему никакого преимущества. Однако при отклонении нескольких игроков эти игроки могут получить больший выигрыш, нежели в ситуации равновесия. В связи с этим в условиях, в которых возможна кооперация между игроками, принцип равновесия не оправдывает себя. Так, например, пусть неантагонистическая игра двух лиц задается двумя матрицами:
 ,
,  .
.
В этой игре  ,
, 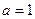 и
и  , поэтому ситуациями приемлемыми для игрока 1, будут ситуации вида
, поэтому ситуациями приемлемыми для игрока 1, будут ситуации вида  при произвольном
при произвольном  . Аналогично для игрока 2 приемлемыми ситуациями будут ситуации вида
. Аналогично для игрока 2 приемлемыми ситуациями будут ситуации вида  при произвольном
при произвольном  . Следовательно, здесь единственной ситуацией равновесия оказывается ситуация (0, 0), в которой каждый из игроков выбирает свою вторую чистую стратегию и выигрывает единицу. Вместе с тем очевидно, что если игроки договариваются и выбирают свои первые чистые стратегии, то в ситуации (1, 1) каждый из них выигрывает по пять единиц. Однако ясно, что ситуация (1, 1), которая может сложиться при возможности кооперирования, является весьма неустойчивой, так как каждый игрок, изменяя в ней произвольным образом свою стратегию, увеличивает свой выигрыш.
. Следовательно, здесь единственной ситуацией равновесия оказывается ситуация (0, 0), в которой каждый из игроков выбирает свою вторую чистую стратегию и выигрывает единицу. Вместе с тем очевидно, что если игроки договариваются и выбирают свои первые чистые стратегии, то в ситуации (1, 1) каждый из них выигрывает по пять единиц. Однако ясно, что ситуация (1, 1), которая может сложиться при возможности кооперирования, является весьма неустойчивой, так как каждый игрок, изменяя в ней произвольным образом свою стратегию, увеличивает свой выигрыш.
Итак, при возможности кооперирования возникает противоречие между устойчивостью ситуации, выражаемой в виде равновесности, и ее целесообразностью – стремлением игроков к большим выигрышам. Это противоречие может разрешаться путем расширения множеств уже имеющихся стратегий на основе тех или иных стратегий между игроками. В частности, игроки могут выбирать свои стратегии совместно, договариваясь между собой. В результате множество ситуаций в смешанных стратегиях будет множеством всех вероятностных мер на множестве всех ситуаций в чистых стратегиях. Напомним, что при отсутствии соглашений между игроками множество ситуаций в смешанных стратегиях являлось произведением вероятностных мер, заданных на чистых стратегиях каждого из игроков.
Обозначим через U множество всевозможных векторов выигрышей игроков в игре n лиц при применении ими всех смешанных стратегий, заданных на множестве всех ситуаций в чистых стратегиях. Множество U содержится в евклидовом пространстве Rn и является выпуклым, так как в рассматриваемом случае функция выигрыша каждого из игроков - линейная функция относительно совместной стратегии игроков, а множество их стратегий является выпуклым. Если предположить непрерывность функции выигрыша на множестве всех ситуаций в чистых стратегиях и компактность этого множества, то множество всех выигрышей будет также замкнуто и ограниченно, а поэтому компактно. Таким образом, при возможности кооперирования и некоторых предположениях о первоначальной бескоалиционный игре игроки имеют перед собой некоторое замкнутое ограниченное и выпуклое подмножество  . Это множество называется допустимым множеством. Действуя совместно, игроки могут получить в качестве вектора выигрышей любой вектор
. Это множество называется допустимым множеством. Действуя совместно, игроки могут получить в качестве вектора выигрышей любой вектор  .
.
Пусть 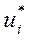 – значение антагонистической игры, в которой все игроки играют против игрока i, т. е. стараются минимизировать его выигрыш, не обращая внимания на свои интересы. Обозначим через
– значение антагонистической игры, в которой все игроки играют против игрока i, т. е. стараются минимизировать его выигрыш, не обращая внимания на свои интересы. Обозначим через  вектор, компоненты которого
вектор, компоненты которого  можно интерпретировать как выигрыши игроков в том случае, когда они не придут к соглашению. Вектор
можно интерпретировать как выигрыши игроков в том случае, когда они не придут к соглашению. Вектор  называют точкой status quo.
называют точкой status quo.
Определение 5.5.Тройку  , где
, где  ,
,  ,
,  – множества игроков, будем называть арбитражной схемой.
– множества игроков, будем называть арбитражной схемой.
Очевидно, игроки (или арбитр) должны руководствоваться некоторыми объективными представлениями о «справедливости» (принцип оптимальности).
2. Принцип оптимальности Нэша для общих арбитражных схем. Сформулируем для арбитражных схем аксиомы 5.1-5.6, которым должно удовлетворять правило  , сопоставляющее каждому выпуклому замкнутому подмножеству U и точке
, сопоставляющее каждому выпуклому замкнутому подмножеству U и точке  точку
точку  .
.
Аксиома 5.1. Реализуемость:  .
.
Аксиома 5.2. Индивидуальная рациональность:  .
.
Аксиома 5.3. Оптимальность по Парето: если  и
и  , то
, то  .
.
Аксиома 5.4. Независимость от посторонних альтернатив: если  и
и  , то
, то  .
.
Аксиома 5.5. Линейность: если множество  получается из U с помощью линейного преобразования, т. е.
получается из U с помощью линейного преобразования, т. е. 
 , а
, а  , то
, то  .
.
Аксиома 5.6. Симметрия: пусть  – произвольная перестановка игроков, для которой
– произвольная перестановка игроков, для которой  следует
следует  . Пусть также
. Пусть также 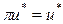 ,
,  . Тогда
. Тогда  .
.
Первые три аксиомы несомненно разумны, и комментарии излишни. Аксиома 5.4 означает, что, имея большие возможности для выбора  , игроки согласятся на этот же вектор выигрышей при меньших возможностях, если этот вектор допустим. Аксиома линейности утверждает, что в разных шкалах измерения полезностей игроки руководствуются одинаковым принципом оптимальности при выборе
, игроки согласятся на этот же вектор выигрышей при меньших возможностях, если этот вектор допустим. Аксиома линейности утверждает, что в разных шкалах измерения полезностей игроки руководствуются одинаковым принципом оптимальности при выборе  . Шестая аксиома (иногда называемая аксиомой анонимности) постулирует равноправие игроков.
. Шестая аксиома (иногда называемая аксиомой анонимности) постулирует равноправие игроков.
Далее для простоты будем считать, что в множестве U существует вектор u, каждая i-я координата которого строго больше  . Противоположный случай тривиален. Оказывается, имеет место следующая теорема:
. Противоположный случай тривиален. Оказывается, имеет место следующая теорема:
Теорема 5.1. Существует единственная функция  , определенная для всех арбитражных схем
, определенная для всех арбитражных схем  и удовлетворяющая аксиомам 5.1 – 5.6. (Доказательство этой теоремы в работе [9]).
и удовлетворяющая аксиомам 5.1 – 5.6. (Доказательство этой теоремы в работе [9]).
Распределение выигрышей согласно функции  имеет ряд существенных недостатков. Основной из них состоит в следующем.
имеет ряд существенных недостатков. Основной из них состоит в следующем.
Пусть имеется некоторое конечное множество игроков 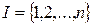 . Любое его подмножество
. Любое его подмножество  , включая само множество I и одноэлементные подмножества
, включая само множество I и одноэлементные подмножества  , а также пустое множество
, а также пустое множество  , называется коалицией. В некоторых случаях коалиция
, называется коалицией. В некоторых случаях коалиция  обеспечивает для всех игроков выигрыши строго большие, чем
обеспечивает для всех игроков выигрыши строго большие, чем  . В этой ситуации игроки кооперативной игры, вступая в соглашения друг с другом, не будут удовлетворены распределением выигрышей
. В этой ситуации игроки кооперативной игры, вступая в соглашения друг с другом, не будут удовлетворены распределением выигрышей  . Поэтому решение о распределении согласно вектору
. Поэтому решение о распределении согласно вектору  может быть принято лишь некоторым третьим лицом – арбитром. Это решение оптимально в смысле аксиом 5. 1 – 5. 6 и носит обязательный характер. Отсюда берут свое название «арбитражные схемы».
может быть принято лишь некоторым третьим лицом – арбитром. Это решение оптимально в смысле аксиом 5. 1 – 5. 6 и носит обязательный характер. Отсюда берут свое название «арбитражные схемы».
|
из
5.00
|
Обсуждение в статье: Решение биматричной игры |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

