Игра с тремя игроками. Устойчивость

1. Продолжим рассмотрение игры из предыдущего раздела для случая 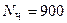и . Как было выяснено, справедливая доля для предприятия «Чайка» в этом случае равна 500, для предприятия «Утро» ‑ 300 и поэтому для предприятия «Сокол» ‑ 1200. Допустим, что «Сокол» берет на себя составление комплектов программных продуктов, вступает в кооперацию с предприятием «Чайка» и заказывает этому предприятию 900 БПО, которые оно в состоянии поставить. Предположим, за эту выгодную для предприятия «Чайка» комбинацию «Сокол» запрашивает с него 175. В итоге «Сокол» получает 900 (от реализации программных продуктов) + 175 (от предприятия «Чайка») = 1075, а «Чайка» ‑ 900 (от реализации программных продуктов) ‑ 175 (предприятию «Сокол») = 725.

Очевидно, что «Сокол» и «Чайка», не выходя за пределы своих производственных возможностей, увеличили свои выигрыши по сравнению со справедливыми долями. Безусловно, это произошло за счет предприятия «Утро». Но для нас важно, что увеличение выигрышей предприятий «Чайка» и «Сокол» происходит не в результате прямого использования ресурсов предприятия «Утро», а за счет его частичного отстранения от сделки. Таким образом, справедливые дележи в рассматриваемой игре не являются устойчивыми. Зададимся целью определить устойчивые дележи (которые, к сожалению, уже не будут справедливыми).

2. Обозначим через , и 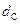доли, которые в некотором дележе получат соответственно «Чайка», «Утро» и «Сокол».

Из условий игры следует, что «Сокол» может заказать предприятию «Чайка» N_Ч БПО. От реализации, комплектов с этим программным обеспечением обе стороны получат по N_Ч. Если 2N_Ч будет больше, чем , то предприятия «Сокол» и «Чайка» смогут разделить 2N_Ч так, чтобы «Сокол» получил больше, чем 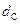, а «Чайка» больше, чем . Таким образом, в этом случае для предприятий «Сокол» и «Чайка», во-первых, выгодно выступить против дележа, в котором они получат дол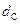и и , a, во-вторых, они имеют технико-экономические возможности это сделать: им достаточно вступить между собой в соглашение и получить 2N_Ч. Следовательно, дележ с долям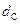и и не будет устойчивым.

Из сказанного видно, что для устойчивости дележа необходимо, чтобы было:

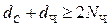(5.4)

Другим необходимым условием является такое же неравенство, касающееся долей предприятий «Сокол» и «Утро»:

(5.5)

Очевидно, что если эти условия выполнены, то дележ будет устойчивым, ибо третья комбинация предприятий («Чайка» и «Утро»), не в состоянии выпустить ни одного комплекта программных продуктов. Их объединение против предприятия «Сокол» ничего не сможет им дать (поэтому такого объединения не возникнет).

3. Для более наглядного описания дележей, удовлетворяющих неравенствам (5.4) и (5.5), удобно прибегнуть к геометрической иллюстрации. Будем откладывать доли предприятий по трем осям координат (рис. 5.1).

Поскольку для любого дележа

(5.6)

и числа 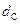, и неотрицательны, каждому дележу будет соответствовать некоторая точка большого треугольника, и наоборот.

Устойчивые дележи, т. е. дележи, удовлетворяющие неравенствам (5.4) и (5.5), соответствуют точкам густо заштрихованного параллелограмма. В теории игр это множество устойчивых дележей называется ядром, или, точнее, С-ядром.

На рис. 5.1 прямые в треугольнике проведены таким образом, что 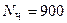, . Крестиком помечена точка, соответствующая справедливому дележу.

Рис 5.1

Сделаем по поводу устойчивых дележей три замечания.

Чем больше числа и (т. е. чем ближе каждое из них к 1000), тем меньше в соответствующем направлении станет заштрихованный параллелограмм устойчивых дележей. Это обстоятельство может выглядеть неожиданным в том же смысле, что и аналогичный факт, отмеченный в связи со справедливым дележом (рост производственных возможностей предприятий «Чайка» и «Утро» уменьшает их доли в устойчивых дележах).

Далее, С-ядро состоит из большого (даже бесконечного) числа дележей, поэтому выбор из них «самого устойчивого», «самого оптимального» представляет собой дальнейшую задачу (которая в данном пособии не рассматривается). С-ядро, очевидно, обладает внутренней устойчивостью: ни от одного дележа из С-ядра невозможно перейти к более предпочтительному. Внешней устойчивостью С-ядро, однако, не обладает: существуют дележи, не принадлежащие С-ядру, вполне конкурентоспособные с дележами из С-ядра, т. е. такие, что переходы от них к каким-либо дележам из С-ядра не сопровождаются увеличением доли предприятия «Сокол» и хотя бы одного предприятия, производящего БПО. Такие дележи составляют редко заштрихованный треугольник.

Чтобы дополнить С-ядро до внешне устойчивого множества, т. е. превратить его в Н-М-решение, можно присоединить к нему «хвост» наподобие изображенного на рис. 5.1, идущий в пределах редко заштрихованного треугольника и отклоняющийся по своему направлению в каждой своей точке от высоты треугольника не более чем на 30°. Такой «хвост» можно присоединить к С-ядру (очевидно, существует большое число способов). Поэтому не только каждое Н-М-решение состоит из большого числа дележей, но и самих Н-М-решений в игре может быть очень много.

Наконец, бывают игры, где устойчивые дележи отсутствуют. В качестве примера рассмотрим игру, в которой, как и ранее, 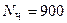, , но, кроме того, предприятия «Чайка» и «Утро» способны, не прибегая к поставкам СПО со стороны предприятия «Сокол», выпустить за счет использования малоэффективного оборудования и технологии 500 комплектов программных продуктов.

В такой игре ни один дележ не будет устойчивым, т. е. не будет входить в С-ядро. Условиями устойчивости являются неравенства (5.4) и (5.5), которые в данном случае приобретают вид , , и аналогичное неравенство, касающееся долей предприятий «Чайка» и «Утро»: (ибо по сделанному предположению 500 комплектов программных продуктов они могут изготовить и без участия предприятия «Сокол»). Складывая эти три неравенства почленно, получаем 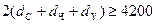, чего, однако, быть не может, так как согласно выражению (5.6) левая часть неравенства равна 4000.

Очевидно, что принцип оптимальности, состоящий в устойчивости дележей, может в некоторых играх оказываться нереализуемым.

БЕСКОАЛИЦИОННЫЕ ИГРЫ

Основы теории

Определение 6.1.Бескоалиционной игрой называется система

Г (6.1)

в которой I и x_i, , являются множествами, H_i – функциями на множестве , принимающими вещественные значения.

При этом элементы множества I – игроки, элементы каждого из множеств x_i – стратегии игрока i, элементы декартова произведения x – ситуации, H_i – функция выигрыша игрока i.

Некоторые рассмотренные выше игры являются частными классами бескоалиционных игр. Так, например, среди явлений, описываемых посредством бескоалиционных игр, довольно много таких, которые сводятся к распределению между игроками некоторого постоянного количества. В теории игр им соответствуют игры с постоянной суммой.

Определение 6.2. Бескоалиционная игра Г называется игрой с постоянной суммой, если существует такое постоянное с, что 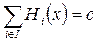для всех ситуаций .

Если для игры Г с постоянной суммой константа с равна нулю, то Г называется игрой с нулевой суммой.

Таким образом, класс антагонистических игр совпадает с классом бескоалиционных игр двух лиц с нулевой суммой (см. гл. 2).

Представляют интерес игры с конечными множествами стратегий игроков.

Определение 6.3. Если в бескоалиционной игре Г множество стратегий x_i каждого из игроков конечно, то игра Г называется конечной.

Конечная игра двух лиц называется биматричной игрой ввиду естественной возможности расположения значений функций выигрыша двух игроков в виде пары матриц (см. гл. 4).

Для бескоалиционных игр разумно ввести понятие приемлемой ситуации. Естественно для игрока считать ситуацию приемлемой, если он, изменяя в ситуации свою стратегию на какую-нибудь другую, не может увеличить своего выигрыша.

Определение 6.4. Ситуация x в игре Г называется приемлемой для игрока i, если для любой его стратегии :

. (6.2)

Множество всех ситуаций, приемлемых в игре Г для игрока i, обозначим через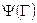

. (6.3)

Согласно определению в ситуациях равновесия и только в них ни один игрок не заинтересован в отклонении от своей стратегии.

Определение 6.5. Равновесной стратегией игрока в бескоалиционной игре называется такая его стратегия, которая входит хотя бы в одну из ситуаций равновесия игры.

В случае антагонистической игры равновесные стратегии игроков совпадают с их оптимальными стратегиями. Для неантагонистических игр, напротив, понятие оптимальной стратегии игрока нередко вообще не имеет смысла: в таких играх оптимальными оказываются не стратегии отдельных игроков, а их сочетания (т. е. ситуации) и притом для множества всех игроков сразу.

В связи с этим в общих бескоалиционных играх как оптимальные следует квалифицировать не действия того или иного игрока, а совокупность действий всех игроков, исход игры, ситуацию в ней.