 |
Главная |
Симметричный трехфазный приемник, соединенный по схеме «звезда»
|
из
5.00
|
Симметричный трехфазный приемник – это приемник, у которого комплексные сопротивления фаз равны между собой 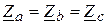 ,т. е. у такого приемника равны между собой модулии аргументы фазных сопротивлений – Za = Zв = Zc,
,т. е. у такого приемника равны между собой модулии аргументы фазных сопротивлений – Za = Zв = Zc,  а =
а =  в =
в =  с.
с.

Рис.8.1. Трехфазный приемник, соединенный по схеме «звезда»
Из формулы следует, что при равенстве комплексных проводимостей фаз междуузловое напряжение будет равно 0, так как
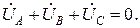
Согласно II ЗК для контуров трехфазной системы:
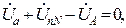
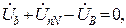
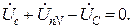
Следовательно, напряжения фаз приемника:
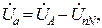
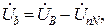
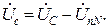
Так как UnN = 0, то для симметричного приемника фазные напряжения приемника равны фазным напряжениям генератора:
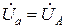 ;
; 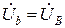 ;
; 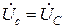
Определив фазные напряжения, находят фазные токи:
İа = 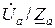 ; İb =
; İb = 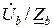 ; İс =
; İс = 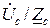 .
.
Для построения векторной диаграммы достаточно задаться начальной фазой одного из напряжений цепи, например jAB= + 30°.
Тогда
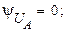
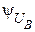 = -120°;
= -120°; 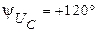 .
.
На комплексной плоскости строятся в масштабе векторы фазных напряжений 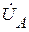 ,
, 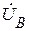 ,
, 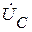 и под углом φ проводятся векторы токов (рис.8.2).
и под углом φ проводятся векторы токов (рис.8.2).
|
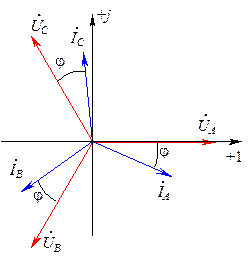
Рис.8.2. Векторная диаграмма симметричного приемника
Симметричный трехфазный приемник подключают к трехпроводной системе.
8.2. Несимметричный трехфазный приемник.
Это приемник, у которого комплексные сопротивления фаз не равны между собой 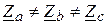 (рис.8.3).
(рис.8.3).

Рис.8.3.Схема несимметричного приемника.
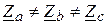 , jа ≠ jb ≠ jc - общий случай,
, jа ≠ jb ≠ jc - общий случай,
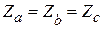 , jа ≠ jb ≠ jc - равномерная несимметричная,
, jа ≠ jb ≠ jc - равномерная несимметричная,
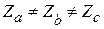 , jа = jb = jc - однородная несимметричная.
, jа = jb = jc - однородная несимметричная.
Как видно из приведенного, у такого приемника могут быть не равны между собой модули фаз, аргументы равны; равны между собой модули фаз, аргументы фаз не равны; не равны между собой как модули так и аргументы фаз. В этом случае напряжение между нейтральной точкой генератора и нейтральной точкой приемника не будет равно нулю.
Фазные напряжения и токи приемника определяются по формулам
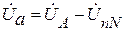 ,
,
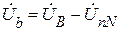 ,
,
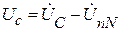 ,
,
где 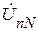 – напряжение смещения нейтрали, которое определяется методом междуузлового напряжения:
– напряжение смещения нейтрали, которое определяется методом междуузлового напряжения:
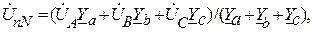
где для приведенной схемы:
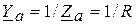 ;
; 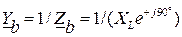 ;
; 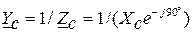 .
.
По закону Ома определяются фазные токи:
İа = 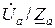 ,
,
İb = 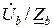 ,
,
İс = 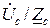 .
.
При построении векторной диаграммы необходимо (рис.8.4) сначала построить векторы напряжений источника 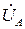 ,
, 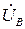 ,
, 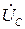 , напряжения
, напряжения
смещения нейтрали 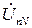 , провести новые оси комплексной плоскости, а
, провести новые оси комплексной плоскости, а
затем построить векторы напряжений приемника 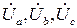 и векторы
и векторы
токов под соответствующими углами ψia, ψib, ψiс или 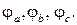
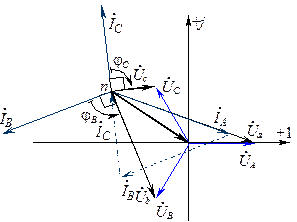
Рис.8.4. Векторная диаграмма напряжений и токов при смещении нейтрали
Из векторной диаграммы следует, что асимметрия нагрузки в трехпроводной сети приводит к перекосу фазных напряжений, что недопустимо. Поэтому трехпроводная система при несимметричной нагрузке и схеме «звезда» не применяется.
Из приведенных формул видно, что фазные напряжения приемника будут отличаться как от фазных напряжений генератора, так и относительно друг друга. В этом случае наступает «перекос» фазных напряжений приемника, что приводит к перенапряжению фаз приемника, токи фаз превышают номинальные значения, что является недопустимым.
В этом случае нарушается симметрия фазных напряжений на приемнике:
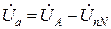 ;
; 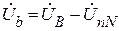 ;
; 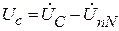 ,
,
где 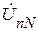 – напряжение смещения нейтрали, которое определяется методом междуузлового напряжения.
– напряжение смещения нейтрали, которое определяется методом междуузлового напряжения.
Анализ формул показывает, что для выравнивания фазных напряжений приемника необходимо получить значение напряжения между нейтральными точками генератора и приемника равное 0. Это возможно при равенстве знаменателя бесконечности, т. е., если принять ZnN = 0, то YnN = ¥. На практике это достигается включением провода, сопротивление которого мало, между нейтралями генератора и приемника. Тогда
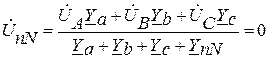 .
.
В этом случае напряжения на фазах приемника остаются практически симметричными, равными напряжению генератора.
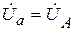 ;
; 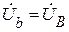 ;
; 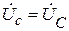 .
.
Для схемы рис.8.5 значения комплексных полных проводимостей:
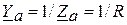 ;
; 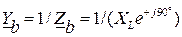 ;
; 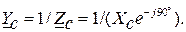
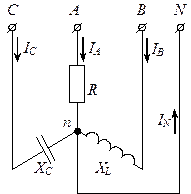
Рис.8.5. Схема несимметричного приемника, включенного в четырех проводную систему
По закону Ома определяются фазные токи:
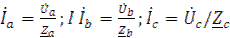
Ток нулевого провода
İN = İa + İb + İc
Векторная диаграмма для цепи приведена на рис.8.6. .
|

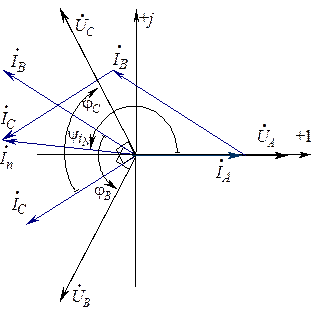
Рис.8.6. Векторная диаграмма несимметричного трехфазного приемника, включенного в четырехпроводную систему
8.3. Соединение фаз приемника по схеме «треугольник»
Схема «треугольник» образуется при соединении начала одной фазы с концом другой, при этом получается замкнутый контур. Начало фазы а приемника соединяют с концомфазы b - y, (точка а). Далее соединяют точки b и z (точка b) иточки с и х (точка с). Начала фаз выводят в линии.(рис.8.7)
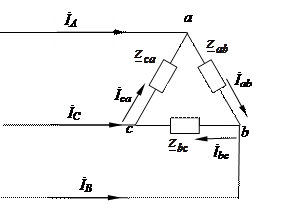 |
Рис.8.7. Схема трехфазного приемника, соединенного по схеме треугольник
По фазам приемника протекают фазные токи İав, İвс, İса. Условное положительное направление фазных токов приемника от начала к концу фаз. Условные положительные направления фазных напряжений совпадают с положительным направлением фазных токов. Условное положительное направление линейных токов İА, İВ, İС принято от генератора к приемнику.
Напряжение между началом и концом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению:
Uл = Uф.
При подключении приемника, соединенного треугольником, к источнику питания по фазам приемника протекает фазный ток, который определяется по закону Ома:
İф= Uф/Zф.
Линейные токи можно определить из уравнений, составленных по II ЗК для точек а, в, с соответственно:
İса – İав + İА = 0; İав – İвс + İВ = 0; İвс – İса + İс = 0.
Таким образом, получаем
İА=İав – İса; İВ=İвс – İав; İс=İса – İвс.
Итак,линейные токи при соединении треугольником равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.
Как следует из вышеприведенных уравнений, векторная сумма линейных токов всегда равна нулю:
İА + İВ + İС = 0.
Система линейных (фазных) токов при соединении треугольником образует такой же замкнутый треугольник, как система линейных (фазных) напряжений и при соединении звездой. Фазные токи при симметричной нагрузке равны по значению и сдвинуты по отношению к векторам напряжений на одинаковый угол φ.
Для определения линейных токов строем векторную диаграмму фазных токов (рис.8.8). Так как линейные токи определяются через фазные так же, как и линейные напряжения через фазные при соединении звездой, то можно сразу построить векторы линейных токов, соединив концы векторов фазных токов.
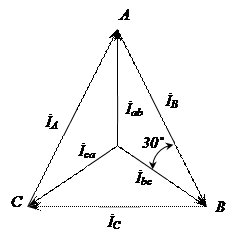 |
.Рис.8.8. Векторная диаграмма фазных и линейных токов при соединении фаз треугольником
Векторы линейных токов образуют замкнутый треугольник. Поскольку при симметричной нагрузке системы фазных и линейных токов симметричны, сравнивая векторные диаграммы токов схемы треугольник и напряжений схемы звезда, можно заключить, что линейные токи при симметричной нагрузке, соединенной треугольником, в 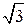 = 1,73 раза больше фазных:
= 1,73 раза больше фазных:
Iл = 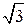 IФ
IФ
8.4. Несимметричная нагрузка при соединении треугольником.
Трехпроводная система. При соединении треугольником Uл = Uф, а линейные напряжения источника всегда симметричны. Поэтому соединение треугольником применяется в трехпроводных системах при любой нагрузке, как симметричной, так и несимметричной, если номинальное напряжение приемника равняется линейному напряжению источника питания (рис.8.9).
|
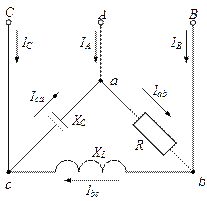
Рис.8.9. Схема несимметричного приемника, соединенного по схеме треугольник
Фазные токи
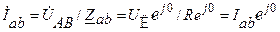 ;
; 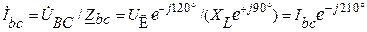 ;
;
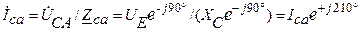 .
.
Линейные токи определяются по II ЗК для узлов a, b, c:
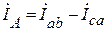 ;
; 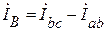 ;
; 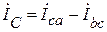 .
.
Для построение векторной диаграммы на комплексной плоскости сначала строятся векторы линейных напряжений, затем векторы фазных токов и по ним определяются графически линейные токи, которые должны совпасть с расчетными по модулю и аргументу (рис.8.10).
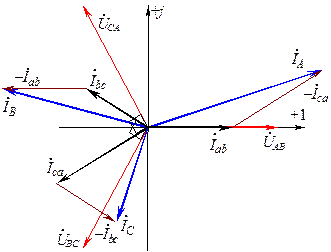
Рис.8.10. Векторная диаграмма напряжений, фазных и линейных токов при
соединении фаз приемника треугольником при несимметричной нагрузке
|
из
5.00
|
Обсуждение в статье: Симметричный трехфазный приемник, соединенный по схеме «звезда» |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


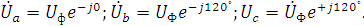 İa = Ua e j0˚/R = Ia e j0˚/;
İb = Ub e -j120˚/XLe +j90˚ = Ibe - j210˚;
İС = UС e+ j120˚/XСe -j90˚ = IС e +j210˚;
İN = İa + İb + İc = IN e+jψiN
İa = Ua e j0˚/R = Ia e j0˚/;
İb = Ub e -j120˚/XLe +j90˚ = Ibe - j210˚;
İС = UС e+ j120˚/XСe -j90˚ = IС e +j210˚;
İN = İa + İb + İc = IN e+jψiN
 . Тогда
. Тогда 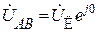 ;
;
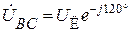 ;
; 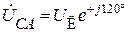 .
Комплексные сопротивления приемника
.
Комплексные сопротивления приемника  ;
; 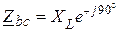 ;
;
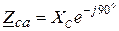 .
.