Теорема деления тензоров (критерий тензорности)

Рассмотрим удобный критерий для характеристики геометрических и физических величин при помощи тензоров. Пусть некоторая величина в прямоугольных координатах и определяется при помощи чисел и соответственно, и пусть для любых трех векторов , , справедливо равенство:

(114)

т.е. левая и правая части равенства – скаляры. Тогда можно показать, что и являются компонентами тензора 3-его ранга относительно координатных систем и соответственно. Для доказательства выразим в равенстве (114) компоненты векторов в старой системе 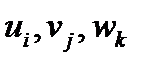через компоненты в новой системе : , , и подставим в (114): , или

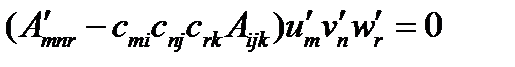(115)

Левая часть этого равенства представляет собой тройную сумму по индексам . Она может тождественно равняться нулю лишь в том случае, когда обращаются в нуль все ее коэффициенты при компонентах векторов, т.е. когда для всех значений индексов выражение в скобках равно нулю: . Отсюда получим: (116)

т.е. величины в старой системе координат преобразуются в величины в новой системе так же, как компоненты тензора 3-его ранга. Аналогично можно провести рассуждения и для обратного перехода от новой системы к старой. Следовательно, приходим к выводу, что – это тензор 3-его ранга.

Аналогично можно показать, что – тензор 3-его ранга, если известно, что есть вектор при любом выборе тензора 2-ого ранга .

Для краткости мы рассмотрели лишь тензор 3-его ранга, но можно получить обобщение для тензоров любого ранга. Изложенный критерий является частным случаем известной в тензорной алгебре теоремы деления тензоров.

§18. - тензор Леви-Чивиты (единичный тензор 3-го ранга).

Во многих случаях очень удобным оказывается использование так называемого символа Леви-Чивиты:

(117)

Круговые перестановки – это 123, 231, 312. Некруговые перестановки – это 132, 213, 321. Следствием этого определения являются следующие соотношения:

(118)

Справедливость их следует из того, что перестановки и являются круговыми из первоначальной перестановки , а перестановки 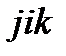, , круговыми не являются.

Приведем полезные соотношения, связанные с символом Леви-Чивиты:

, , (119)

Рассмотрим применение символа Леви-Чивиты. Как известно из курса векторной алгебры, смешанное произведение трех векторов записывается в виде определителя:

(120)

С помощью символа Леви-Чивиты смешанное произведение записывается компактно:

(121)

Чтобы доказать это, проведем суммирование по индексам , принимая во внимание определение (117):

С другой стороны, если раскрыть определитель (120), то получим то же самое.

Как известно, смешанное произведение, т.е. определитель (120), положительно, если тройка перемножаемых векторов 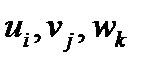и тройка базисных векторов имеют одинаковую ориентацию (например, обе – правые). В противном случае смешанное произведение отрицательно. Отсюда следует, что при переходе от правой системы координат к левой и наоборот, смешанное произведение меняет знак. Такие величины называются псевдоскалярами, в отличие от истинных скаляров, которые не меняются при любых преобразованиях. В частности, модуль смешанного произведения, т.е. объем параллелепипеда, построенного на перемножаемых векторах, является истинным скаляром.

Выведем закон преобразования символа Леви-Чивиты при преобразованиях координат. Обозначим компоненты символа Леви-Чивиты в новой координатной системе через , а компоненты векторов, участвующих в смешанном произведении, через 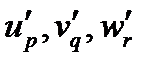. В новой координатной системе смешанное произведение запишется как , и имеет место равенство:

, (122)

где знак плюс берется, если при преобразовании координат ориентация базисных векторов не меняет знак, и знак минус – в противном случае. Вспоминая закон преобразования векторов (формулы (40), (41)), получим из (122): , или .

Рассуждая теперь так же, как в параграфе 17, получим:

(123)

Аналогично получается и обратная формула:

(124)

Этими формулами определяется закон преобразования символа Леви-Чивиты. С точностью до знака он совпадает с законом преобразования тензора 3-его ранга.

Если при преобразовании ориентация системы координат не меняется, т.е. если, например, правая система остается правой, то в формулах (123) и (124) нужно брать знак плюс, если же правая система переходит в левую, или наоборот, – то знак минус. Геометрический объект, преобразующийся по формулам (123) и (124), называется псевдотензором, в данном случае 3-его ранга. Если ограничиться только правыми системами координат, что мы и будем подразумевать в дальнейшем за небольшими исключениями, то символ Леви-Чивиты будет истинным тензором 3-его ранга. Он так и называется тензором Леви-Чивиты или 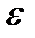- тензором. Из определений (117) и (118) следует, что 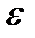- тензор является полностью антисимметричным по всем трем индексам.

Векторное произведение тоже очень просто записывается с помощью 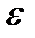- тензора:

(125)

В курсе линейной алгебры векторное произведение определялось как вектор. Это не совсем так с точки зрения определения вектора, данного в параграфе 2. Там мы определяли вектор как объект, компоненты которого преобразуются по формулам (40), (41). Найдем закон преобразования компонент векторного произведения, имея в виду, что символ Леви-Чивиты преобразуется по формулам (123), (124), а векторы – по формулам (40), (41):

Поскольку в новой системе координат векторное произведение определяется той же формулой (125), то , и тогда

(126)

Аналогично получаем формулу обратного перехода, тоже с двумя знаками: плюс и минус:

(127)

Рис. 9а)

Таким образом, векторное произведение в действительности является псевдовектором. Псевдовекторы иначе называются аксиальными векторами. Истинные векторы, которые преобразуются согласно формулам (40), (41), называются иначе полярными векторами, когда необходимо провести четкое различие между двумя этими типами векторов.

Примерами аксиальных или псевдовекторов являются угловая скорость, момент количества движения, момент силы, ротор полярного вектора, напряженность и индукция магнитного поля. В то время как перемещение, скорость, ускорение, сила – это все полярные векторы. Аксиальный вектор характеризует вращение вокруг некоторой оси и поэтому изображается отрезком прямой определенной длины параллельно оси с указанием направления вращения вокруг оси. На рис. 9 показано символическое изображение полярного вектора (а) и аксиального вектора (б):

Рис. 9б)

Чтобы пояснить различие между двумя этими типами векторов, отразим каждый символ на рис. 9 в плоскости, перпендикулярной их длине. Символ, изображающий полярный вектор, изменит направление на обратное, а символ аксиального вектора останется неизменным. Если же отразить каждый символ в плоскости, параллельной их длине, то результат будет обратным.

Допустим, что мы перешли от правой системы координат к левой посредством преобразования , т.е. изменили направление всех осей напротивоположные (рис. 10). Новые компоненты полярного вектора будут равны:

(128)

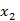Рис. 10

т.е. все компоненты изменят знак. Для аксиального вектора:

(129)

т.е. аксиальный вектор не изменился.

Подчеркнем еще раз, что если ограничиться только правосторонними системами координат, то различия между полярными и аксиальными векторами, а также вообще между тензорами и псевдотензорами нет.

Бивектор.

Антисимметричный тензор 2-ого ранга называется иначе бивектором. Такое название проистекает из того, что этому тензору можно поставить в соответствие вектор (точнее аксиальный вектор, т.е. псевдовектор). Пусть – антисимметричный тензор 2-го ранга. Его матрица имеет вид:

(130)

Такой тензор имеет всего три, как говорят, существенные компоненты . Найдем компоненты тензора в какой-либо другой системе, используя закон преобразования тензоров 2-ого ранга (70) и принимая во внимание его антисимметричность:

(131)

Как было показано в параграфе 12, свойство антисимметричности не зависит от системы координат. Поэтому и в новой системе существенными будут только три компоненты:

(132)

Проанализируем сначала первую из этих формул. В правой части в скобках выражения равны минорам элементов третьей строки матрицы преобразования (см. §3):

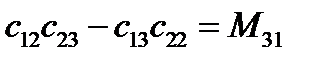, , (133)

или, заменяя миноры алгебраическими дополнениями , получим:

(134)

Аналогично для двух других существенных компонент получим:

, (135)

В задаче 6 параграфа 8 было показано, что каждый элемент матрицы преобразования равен с точностью до знака своему алгебраическому дополнению. С учетом этого получаем:

,

(136)

Если при преобразовании координат ориентация новой системы не изменится, то в (136) следует брать знак плюс. Тогда:

(137)

Эти выражения напоминают закон преобразования компонент вектора. Последнее будет особенно заметно, если переобозначить существенные компоненты тензора так: , , 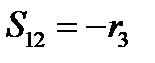. Соответственно в новой системе: , , . Тогда формулы (137) принимают знакомый вид:

(138)

или коротко: (139)

Если же ориентация новой системы изменилась, то:

(140)

Объединяя эти две формулы, окончательно получим:

(141)

Теперь видно, что три величины являются компонентами аксиального вектора. Матрица антисимметричного тензора 2-ого ранга (бивектора) выглядит теперь так:

(142)

Таким образом, всякий антисимметричный тензор 2-ого ранга эквивалентен аксиальному вектору. В правосторонних системах координат это будет истинный вектор. Используя - тензор, связь между вектором и бивектором можно записать так:

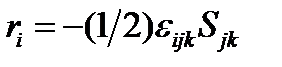(143)

Чтобы убедиться в этом, распишем подробно:

. Тогда: , , , что совпадает с введенными выше компонентами вектора .

По формуле (143) можно найти аксиальный вектор , зная бивектор . Можно получить и обратную формулу. Для этого умножим обе части (143) на : .

Воспользуемся третьей формулой (119):

или с учетом антисимметричности 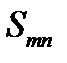: . Окончательно: (144)

Эта формула позволяет найти бивектор , если известен вектор .