 |
Главная |
Симметричного тензора второго ранга
|
из
5.00
|
Определение. Направление, определяемое единичным вектором  , называется главным направлением симметричного тензора 2-го ранга
, называется главным направлением симметричного тензора 2-го ранга  , если вектор
, если вектор  коллинеарен вектору
коллинеарен вектору 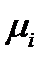 . Это можно записать в виде:
. Это можно записать в виде:
 (158)
(158)
Число  называется главным значением тензора
называется главным значением тензора  . С помощью тождества
. С помощью тождества  соотношению (158) можно придать форму:
соотношению (158) можно придать форму:
 , (159)
, (159)
которая представляет систему трех уравнений для неизвестных компонент 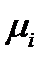 . В развернутой записи эта система имеет вид:
. В развернутой записи эта система имеет вид:
 (160)
(160)
Это однородная линейная система. Из курса линейной алгебры известно, что она всегда имеет тривиальное решение  , однако нашей целью является получение нетривиального решения. Известно, что если нетривиальное решение существует, то таких решений не одно, а бесконечно много. Нас интересует решение, определяющее единичный вектор, т.е. удовлетворяющее условию
, однако нашей целью является получение нетривиального решения. Известно, что если нетривиальное решение существует, то таких решений не одно, а бесконечно много. Нас интересует решение, определяющее единичный вектор, т.е. удовлетворяющее условию  . Условием существования нетривиального решения является равенство нулю определителя системы (160), т.е.
. Условием существования нетривиального решения является равенство нулю определителя системы (160), т.е.
 (161)
(161)
Сокращенно формулу (161) запишем так:
 (162)
(162)
Выражение (161) определяет уравнение относительно неизвестного  . Корни этого уравнения являются главными значениями тензора
. Корни этого уравнения являются главными значениями тензора  . Если развернуть определитель в (161), то получим кубическое уравнение относительно
. Если развернуть определитель в (161), то получим кубическое уравнение относительно  , которое называется характеристическимуравнением симметричного тензора
, которое называется характеристическимуравнением симметричного тензора  и записывается в виде:
и записывается в виде:
 (163)
(163)
Так как корни этого уравнения являются скалярами, не зависящими от системы координат, то коэффициенты характеристического уравнения  ,
,  ,
,  также не зависят от системы координат, т.е. тоже скаляры. Они называются главными инвариантами симметричного тензора
также не зависят от системы координат, т.е. тоже скаляры. Они называются главными инвариантами симметричного тензора  . Первый главный инвариант:
. Первый главный инвариант:
 (164)
(164)
– это знакомый нам след тензора  . Второй инвариант
. Второй инвариант  равен
равен
сумме миноров элементов главной диагонали матрицы тензора, взя-
той со знаком минус, т.е.:
 (165)
(165)
Можно показать, что он равен:
 (166)
(166)
Наконец, третий инвариант  представляет собой определитель матрицы тензора, т.е.:
представляет собой определитель матрицы тензора, т.е.:
 (167)
(167)
Характеристическое уравнение (163) имеет три корня, причем хотя бы один из них – действительный. Это следует из того, что поскольку коэффициенты уравнения (т.е. главные инварианты) действительны, то комплексные корни появляются парами, как комплексно-сопряженные числа. Значит три корня характеристического уравнения либо все действительные, либо один действительный, а два других – комплексно-сопряженные.
Обозначим действительное главное значение через  . Подставляя в (160), решаем систему и находим одно главное направление
. Подставляя в (160), решаем систему и находим одно главное направление  . Примем теперь его за ось
. Примем теперь его за ось  новой системы координат и найдем компоненты тензора
новой системы координат и найдем компоненты тензора  в новой системе. Подставим
в новой системе. Подставим  и
и 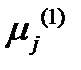 в уравнение (158), а компоненты тензора отнесем к новой системе, тогда получим:
в уравнение (158), а компоненты тензора отнесем к новой системе, тогда получим:
 (168)
(168)
Компоненты вектора  в новой системе
в новой системе  ,
,  , или коротко
, или коротко  . Подставив в (168), получим:
. Подставив в (168), получим: 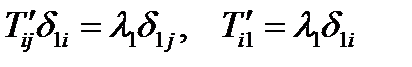 , Отсюда:
, Отсюда:  (169)
(169)
В новой системе координат характеристическое уравнение (161) сохраняет свой вид, только компоненты тензора заменяются на  . С учетом (169) уравнение (161) будет выглядеть так:
. С учетом (169) уравнение (161) будет выглядеть так:
 (170)
(170)
Раскрыв определитель, получим:
 , или
, или
 , или
, или
 .
.
Такой вид приняло характеристическое уравнение (163) в новой системе. Из него получаем, во-первых, уже найденное главное значение  , а во-вторых, два других главных значения определяются как корни квадратного уравнения:
, а во-вторых, два других главных значения определяются как корни квадратного уравнения:
 (171)
(171)
Его дискриминант равен:
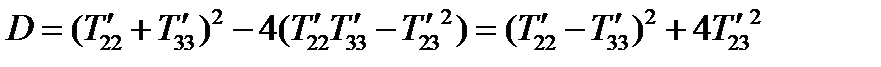 (172)
(172)
Видно, что дискриминант неотрицателен, поэтому корни уравнения (171) действительны. Следовательно, приходим к важному выводу, что все три главных значения симметричного тензора действительны.
Допустим, что нашли два других главных значения 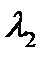 и
и  . Подставляя их последовательно в (160) и решая систему, найдем еще два главных направления
. Подставляя их последовательно в (160) и решая систему, найдем еще два главных направления 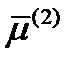 ,
,  . Покажем, что главные направления ортогональны между собой, если главные значения различны. Подставив главные значения
. Покажем, что главные направления ортогональны между собой, если главные значения различны. Подставив главные значения 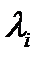 и векторы главных направлений
и векторы главных направлений  в уравнение (159), получим:
в уравнение (159), получим:
 ,
,  ,
, 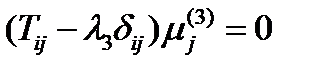 .
.
Умножим первое уравнение на  , второе – на
, второе – на 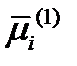 и вычтем их друг из друга:
и вычтем их друг из друга:  , или, раскрывая скобки и приводя подобные члены:
, или, раскрывая скобки и приводя подобные члены:  , или
, или
 . (173)
. (173)
Если  , то получим:
, то получим:
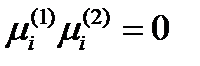 (174)
(174)
Это скалярное произведение, и равенство его нулю означает, что 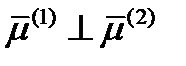 . Аналогично доказывается ортогональность других главных направлений между собой. Таким образом, приходим к еще одному важному выводу: главные направления, соответствующие различным главным значениям, ортогональны. Из этого вытекает важное следствие: если главные значения
. Аналогично доказывается ортогональность других главных направлений между собой. Таким образом, приходим к еще одному важному выводу: главные направления, соответствующие различным главным значениям, ортогональны. Из этого вытекает важное следствие: если главные значения  ,
,  ,
,  являются различными, то главные направления определяются однозначно. Действительно, допустив противоположное, т.е. многозначность, получим, что каждое первое главное направление должно быть ортогонально каждому второму и каждому третьему главным направлениям, а каждое второе ортогонально каждому третьему. Это противоречит тому, что в трехмерном пространстве не может быть более трех взаимно ортогональных направлений.
являются различными, то главные направления определяются однозначно. Действительно, допустив противоположное, т.е. многозначность, получим, что каждое первое главное направление должно быть ортогонально каждому второму и каждому третьему главным направлениям, а каждое второе ортогонально каждому третьему. Это противоречит тому, что в трехмерном пространстве не может быть более трех взаимно ортогональных направлений.
Тензор с различными главными значениями  ,
,  ,
,  и соответствующими главными направлениями
и соответствующими главными направлениями  ,
,  ,
,  можно записать в виде:
можно записать в виде:
 (175)
(175)
Чтобы показать справедливость этого, посмотрим, какой вектор сопоставляется, например, главному направлению  :
:

В силу ортогональности главных направлений скалярные произведения  ,
,  , а скалярное произведение
, а скалярное произведение 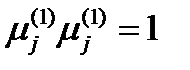 . Тогда получим, что
. Тогда получим, что  , т.е. главному направлению
, т.е. главному направлению  сопоставляется коллинеарный вектор, как и должно, быть. Аналогично показывается для главных направлений
сопоставляется коллинеарный вектор, как и должно, быть. Аналогично показывается для главных направлений  и
и 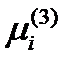 .
.
Направим теперь новые оси координат по трем главным направлениям и посмотрим, какова будет матрица тензора в новой системе. Ось  направим по направлению
направим по направлению  . Тогда вектор
. Тогда вектор  будет иметь компоненты:
будет иметь компоненты: 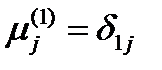
 Ось
Ось  направляем вдоль
направляем вдоль  . Вектор
. Вектор  будет иметь компоненты:
будет иметь компоненты:  . Ось
. Ось 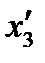 направляем вдоль
направляем вдоль 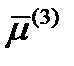 . Тогда
. Тогда  . Подставляя все это в (175), получим:
. Подставляя все это в (175), получим:
 (176)
(176)
Отсюда  ,
, 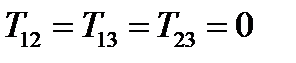 ,
, 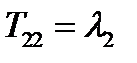 ,
,  .Следовательно:
.Следовательно:
 (177)
(177)
т.е. матрица тензора в главных осях диагональна. Верно и обратное: три взаимно ортогональных оси являются главными осями симметричного тензора 2-го ранга, если матрица этого тензора в системе координат, составленной из главных осей, принимает диагональную форму. В случае трех различных главных значений существует только одна система главных осей.
Мы исследовали случай,когда дискриминант (172) строго положителен. Пусть теперь он равен нулю. Это означает, что два главных значения, отличных от  , равны друг другу, т.е.
, равны друг другу, т.е.  . Как видно из (172), условие
. Как видно из (172), условие 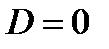 выполняется, если
выполняется, если  . Характеристическое уравнение (171) при этом принимает вид:
. Характеристическое уравнение (171) при этом принимает вид:  , или
, или  . (178)
. (178)
Отсюда: 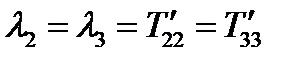 . (179)
. (179)
Найдем теперь главные направления, соответствующие главным значениям  и
и  . Направим ось
. Направим ось  вдоль ранее найденного главного направления
вдоль ранее найденного главного направления  , а оси
, а оси  ,
,  произвольно, но перпендикулярно к
произвольно, но перпендикулярно к  . В такой системе координат характеристическое уравнение имеет вид (170), а система уравнений (160) принимает вид с главным значением
. В такой системе координат характеристическое уравнение имеет вид (170), а система уравнений (160) принимает вид с главным значением  :
:
 (180)
(180)
В силу (179) два последних уравнения выполняются тождественно при произвольных значениях  ,
,  .
.

|

|

|
| Рис. 11 |
 , имеем:
, имеем: 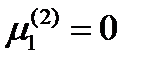 . Итак, главное направление
. Итак, главное направление  определяется компонентами
определяется компонентами 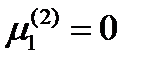 ,
,  и
и  – любые в пределах условия:
– любые в пределах условия:  , которое означает единичность вектора
, которое означает единичность вектора  . Из того, что первая компонента
. Из того, что первая компонента  равна нулю, следует, что вектор
равна нулю, следует, что вектор  перпендикулярен вектору
перпендикулярен вектору  , т.е. главным направлением является любое направление, перпендикулярное вектору
, т.е. главным направлением является любое направление, перпендикулярное вектору  , т.е. лежащее в плоскости, перпендикулярной
, т.е. лежащее в плоскости, перпендикулярной  . Третье главное направление
. Третье главное направление  определяется однозначно, как лежащее в той же плоскости и перпендикулярное
определяется однозначно, как лежащее в той же плоскости и перпендикулярное  . Таким образом, если
. Таким образом, если  , то имеется целая плоскость главных направлений, перпендикулярная главному направлению
, то имеется целая плоскость главных направлений, перпендикулярная главному направлению  (рис 11).
(рис 11).
Следовательно, мы имеем однопараметрическое семейство главных осей, которые можно получить одну из другой вращением вокруг первой главной оси. Обозначим через  – главное значение, соответствующее главному направлению
– главное значение, соответствующее главному направлению  , а через
, а через  – главное значение, соответствующее плоскости главных направлений. Тогда тензор
– главное значение, соответствующее плоскости главных направлений. Тогда тензор  можно записать в виде:
можно записать в виде:
 (181)
(181)
Справедливость этого представления докажем тем, что найдем векторы, которые сопоставляются главным направлениям. Начнем с главного направления  :
:
 .
.
Здесь мы использовали тот факт, что скалярное произведение  . Получили, что направлению
. Получили, что направлению  сопоставляется коллинеарный ему вектор, как и должно быть. Возьмем теперь произвольное направление
сопоставляется коллинеарный ему вектор, как и должно быть. Возьмем теперь произвольное направление  , перпендикулярное
, перпендикулярное  , т.е.
, т.е.  :
:
 , т.е. получили вектор, коллинеарный
, т.е. получили вектор, коллинеарный  .
.
Выясним теперь, какова матрица тензора в системе главных осей. Пусть ось  направлена вдоль
направлена вдоль  , а две другие оси находятся в плоскости, перпендикулярной
, а две другие оси находятся в плоскости, перпендикулярной  . Тогда компоненты
. Тогда компоненты  ,
,  , т.е.
, т.е.  . Подставив в (181), получим:
. Подставив в (181), получим:
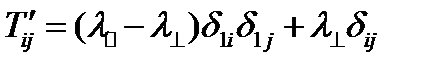 . Отсюда:
. Отсюда:
 ,
,  ,
,  ,
,  ,
,  .
.
Таким образом, в любой системе координат, когда ось  направлена вдоль первого главного направления, а оси
направлена вдоль первого главного направления, а оси  и
и  произвольно в перпендикулярной плоскости, матрица тензора имеет вид:
произвольно в перпендикулярной плоскости, матрица тензора имеет вид:
 (182)
(182)
Определение: Тензор, у которого два главных значения одинаковы, называется трансверсально-изотропным или поперечно-изотропным.
Рассмотрим теперь третий случай, когда все три главных значения одинаковы, т.е.  . Из (179) имеем
. Из (179) имеем  . Система уравнений (180) в этом случае удовлетворяется тождественно. В предыдущем случае два вторых уравнения (180) тождественно удовлетворялись, а теперь удовлетворяется и первое из них. Отсюда следует, что компоненты главных направлений могут быть совершенно любыми, лишь бы соблюдалась единичность направления. Иными словами, любое направление в пространстве будет главным и любая система ортогональных осей – системой главных осей. Тензор в этом случае в любой системе координат представляется в виде:
. Система уравнений (180) в этом случае удовлетворяется тождественно. В предыдущем случае два вторых уравнения (180) тождественно удовлетворялись, а теперь удовлетворяется и первое из них. Отсюда следует, что компоненты главных направлений могут быть совершенно любыми, лишь бы соблюдалась единичность направления. Иными словами, любое направление в пространстве будет главным и любая система ортогональных осей – системой главных осей. Тензор в этом случае в любой системе координат представляется в виде:
 (183)
(183)
или сокращенно:  (184)
(184)
Такой тензор называется шаровым или изотропным.
|
из
5.00
|
Обсуждение в статье: Симметричного тензора второго ранга |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

