 |
Главная |
Векторное произведение как антисимметричный тензор
|
из
5.00
|
Векторное произведение двух векторов впервые появилось при изучении векторной алгебры и определялось там, как вектор, поставленный в соответствие по определенному правилу перемножаемым векторам. Познакомившись с понятием тензора, мы увидели, что в действительности векторное произведение – псевдовектор (аксиальный вектор). В тензорном анализе векторное произведение векторов  и
и  часто определяют как величину:
часто определяют как величину:
 (149)
(149)
Видим, что это удвоенная антисимметричная часть диады  , взятая со знаком минус, и потому являющаяся антисимметричным тензором 2-го ранга (бивектором). Три существенные компоненты этого бивектора являются компонентами векторного произведения в смысле определения векторной алгебры. В самом деле, матрица бивектора (149) выглядит так:
, взятая со знаком минус, и потому являющаяся антисимметричным тензором 2-го ранга (бивектором). Три существенные компоненты этого бивектора являются компонентами векторного произведения в смысле определения векторной алгебры. В самом деле, матрица бивектора (149) выглядит так:
 (150)
(150)
В параграфе 19 формулой (142) мы обозначили существенные компоненты бивектора как  . Сравнивая (150) и (142) видим, что:
. Сравнивая (150) и (142) видим, что:  ;
; 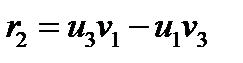 ;
;  (151)
(151)
А это и есть компоненты векторного произведения, как они были определены в векторной алгебре. Следовательно, векторное произведение двух векторов – это бивектор вида (149).
Задачи.
Задача 13. Расшифровать следующие тензорные символы:  ,
,  ,
, 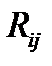 ,
,  ,
,  .
.
Решение. а)  представляет собой сумму:
представляет собой сумму:  и получается свёрткой тензора 2-ранга
и получается свёрткой тензора 2-ранга  . Она называется следом тензора
. Она называется следом тензора 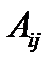 и обозначается
и обозначается  или
или 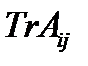 . След тензора 2-ого ранга равен сумме его диагональных компонент.
. След тензора 2-ого ранга равен сумме его диагональных компонент.
б)  – это свертка тензора третьего ранга
– это свертка тензора третьего ранга  по двум последним индексам. Она равна
по двум последним индексам. Она равна  . Результат этой свертки является тензором 1-ого ранга (вектором).
. Результат этой свертки является тензором 1-ого ранга (вектором).
в) 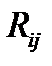 – это тензор 2-ого ранга. Он имеет девять компонент:
– это тензор 2-ого ранга. Он имеет девять компонент:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 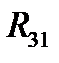 ,
,  ,
,  .
.
г)  – получается в результате свертки произведения вектора
– получается в результате свертки произведения вектора  и тензора 2-ого ранга
и тензора 2-ого ранга 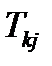 (
(  ). Это произведение является тензором 3-его ранга. В результате свертки по индексам
). Это произведение является тензором 3-его ранга. В результате свертки по индексам  и
и  получается тензор, ранг которого меньше на два, т.е. тензор 1-ого ранга (вектор). В подробной записи это будет так:
получается тензор, ранг которого меньше на два, т.е. тензор 1-ого ранга (вектор). В подробной записи это будет так:  .
.
д) Рассмотрим произведение векторов  ,
,  и тензора 2-ого ранга
и тензора 2-ого ранга  . Получим тензор 4-ого ранга
. Получим тензор 4-ого ранга  . Произведем свертку по парам индексов
. Произведем свертку по парам индексов  и
и 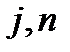 :
:  . Суммируем по индексу
. Суммируем по индексу  :
:  и далее по индексу
и далее по индексу 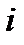 . В результате получаем тензор нулевого ранга (скаляр):
. В результате получаем тензор нулевого ранга (скаляр):
 .
.
Задача 14. Показать, что сумма  является тензором 2-ого ранга, если известно, что
является тензором 2-ого ранга, если известно, что  и
и  – тензоры 2-ого ранга.
– тензоры 2-ого ранга.
Решение. При переходе к новой системе координат тензоры  и
и  преобразуются по закону, выраженному формулами (70), (72). Применяя формулу (72), получим:
преобразуются по закону, выраженному формулами (70), (72). Применяя формулу (72), получим: 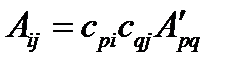 ,
,  . Отсюда:
. Отсюда:  , а это значит, что указанная сумма преобразуется как тензор 2-ого ранга.
, а это значит, что указанная сумма преобразуется как тензор 2-ого ранга.
Задача 15. Показать, что  .
.
Решение. В выражении  все индексы являются немыми. Поскольку немые индексы можно обозначить любыми буквами, во втором слагаемом заменим индексы следующим образом:
все индексы являются немыми. Поскольку немые индексы можно обозначить любыми буквами, во втором слагаемом заменим индексы следующим образом:  . Тогда второе слагаемое примет вид:
. Тогда второе слагаемое примет вид:  . В третьем слагаемом немые индексы переобозначим так:
. В третьем слагаемом немые индексы переобозначим так:  . Тогда третье слагаемое будет иметь вид:
. Тогда третье слагаемое будет иметь вид:  . В результате получаем:
. В результате получаем:
 .
.
Задача 16.  – симметричный,
– симметричный,  – антисимметричный тензоры. Показать, что
– антисимметричный тензоры. Показать, что  .
.
Решение. Так как  и
и  , то
, то 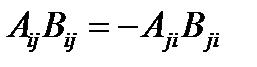 и
и  . Поскольку все индексы являются немыми, то во втором слагаемом переобозначим индексы так:
. Поскольку все индексы являются немыми, то во втором слагаемом переобозначим индексы так: 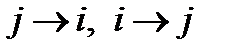 . Тогда
. Тогда  . Отсюда
. Отсюда  .
.
Задача 17. Показать, что свернутое произведение  произвольного тензора
произвольного тензора  с симметричным тензором
с симметричным тензором  не зависит от антисимметричной части
не зависит от антисимметричной части  .
.
Решение. Разложим тензор  на симметричную и антисимметричную части:
на симметричную и антисимметричную части:  .
.
Тогда  . В силу предыдущей задачи
. В силу предыдущей задачи  , поэтому свертка
, поэтому свертка  содержит только симметричную часть тензора
содержит только симметричную часть тензора 

Задача 18. Пусть физическая величина определена в прямоугольной системе координат двадцатью семью числами  . Пусть при переходе к другой системе координат величина
. Пусть при переходе к другой системе координат величина  преобразуется как вектор при любом выборе тензора
преобразуется как вектор при любом выборе тензора  . Доказать, что величины
. Доказать, что величины  представляют собой компоненты тензора 3-его ранга (один из вариантов теоремы деления тензоров).
представляют собой компоненты тензора 3-его ранга (один из вариантов теоремы деления тензоров).
Решение. Обозначим через  вектор
вектор  . В другой системе координат этот же вектор будет иметь компоненты
. В другой системе координат этот же вектор будет иметь компоненты  , равные
, равные  . Поскольку нам известно, что
. Поскольку нам известно, что  – это тензор 2-ого ранга, а
– это тензор 2-ого ранга, а  – вектор, то
– вектор, то  ;
;  . Тогда
. Тогда  . Умножив обе части на
. Умножив обе части на  , получим:
, получим:  . Отсюда
. Отсюда  . С другой стороны
. С другой стороны  . Тогда
. Тогда 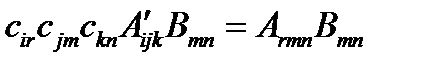 и
и  . Это равенство может выполняться для произвольного тензора
. Это равенство может выполняться для произвольного тензора 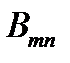 только в том случае, если коэффициенты при компонентах
только в том случае, если коэффициенты при компонентах 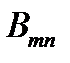 равны нулю. Отсюда получаем:
равны нулю. Отсюда получаем:  . Умножим обе части этого равенства на
. Умножим обе части этого равенства на  :
:  , или
, или 
 , т.е.
, т.е. 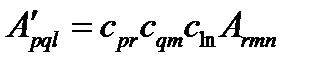 .
.
Видим, что величины  и
и  преобразуются друг в друга как компоненты тензора 3-его ранга.
преобразуются друг в друга как компоненты тензора 3-его ранга.
Задача 19. Доказать формулу (119) для  - тензора.
- тензора.
Решение. а)  . Здесь производится свертка по всем трем индексам. Распишем ее подробно, пользуясь определением символа Леви-Чивитты (117), (118).
. Здесь производится свертка по всем трем индексам. Распишем ее подробно, пользуясь определением символа Леви-Чивитты (117), (118).

б)  . Здесь производится свертка по двум парам индексов. В подробной записи:
. Здесь производится свертка по двум парам индексов. В подробной записи:
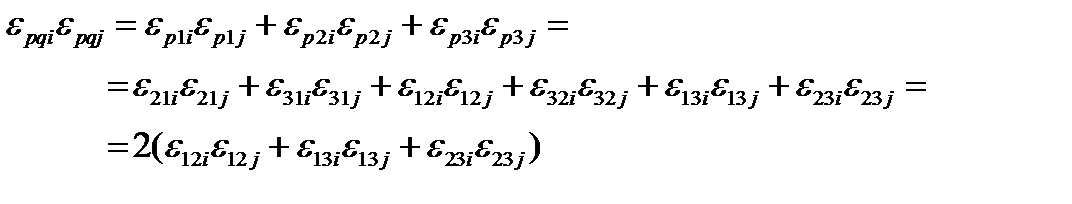
Каждое слагаемое по отдельности в скобках равно:
 ,
,  ,
,
 .
.
Поэтому 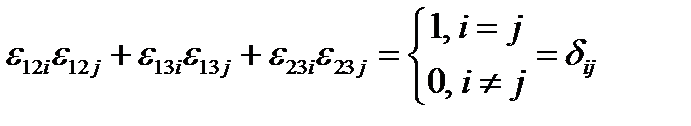 . Отсюда
. Отсюда  .
.
Чтобы доказать третью формулу (119), вначале докажем вспомогательное тождество.
Задача 20. Доказать тождество:
 (151)
(151)
Решение. Для доказательства рассмотрим определитель:
 (152)
(152)
Известно, что перестановка строк и столбцов ведет к изменению знака определителя. Например,
 .
.
Если менять местами строки произвольное число раз, то  . А если менять местами столбцы, то
. А если менять местами столбцы, то  .
.
Следовательно, для произвольной последовательности перестановок строк и столбцов получим:
 (153)
(153)
Положим в определителе (152)  :
:
 . Определитель (153) при этом примет вид:
. Определитель (153) при этом примет вид: 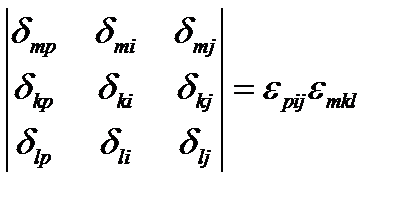 , ч.т.д.
, ч.т.д.
Задача 21. Используя тождество (151), доказать третью формулу (119), т.е.  .
.
Решение. Разложим определитель в (151) по элементам первой строки:

Положим теперь 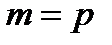 :
:
 ч.т.д.
ч.т.д.
Задача 22. Пользуясь свойствами и определением 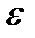 - тензора, доказать основные свойства векторного произведения.
- тензора, доказать основные свойства векторного произведения.
Решение. В параграфе 18 показано, что векторное произведение векторов 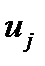 и
и  может быть записано так:
может быть записано так:  (154)
(154)
а) Покажем, что векторное произведение ортогонально к своим сомножителям. Умножим обе части (154), например, на 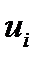 :
:

Скалярное произведение  равно нулю, а это и означает, что векторное произведение
равно нулю, а это и означает, что векторное произведение  ортогонально вектору
ортогонально вектору  Аналогично доказываем, что векторное произведение ортогонально и второму сомножителю
Аналогично доказываем, что векторное произведение ортогонально и второму сомножителю  .
.
б) Докажем антикоммутативность векторного произведения. Векторное произведение 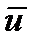 на вектор
на вектор  определено формулой (154). Векторное произведение вектора
определено формулой (154). Векторное произведение вектора  на вектор
на вектор 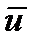 будет равно:
будет равно:  , ч.т.д.
, ч.т.д.
в). Найдем модуль векторного произведения. Умножив обе части (154) на  , получим квадрат модуля:
, получим квадрат модуля:  .
.
В соответствии с формулой (121) в правой части стоит смешанное произведение векторов  ,
,  ,
, 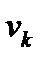 . Как известно, оно равно алгебраическому значению объема параллелепипеда, построенного на этих векторах. Поскольку в левой части стоит квадрат модуля, то правая часть положительна и векторы
. Как известно, оно равно алгебраическому значению объема параллелепипеда, построенного на этих векторах. Поскольку в левой части стоит квадрат модуля, то правая часть положительна и векторы  ,
,  ,
, 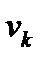 образуют правую тройку (если система координат правая). Кроме того, как было показано в п. а), ребро
образуют правую тройку (если система координат правая). Кроме того, как было показано в п. а), ребро  параллелепипеда ортогонально основанию, образованному векторами
параллелепипеда ортогонально основанию, образованному векторами  и
и 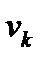 . Поэтому объем параллелепипеда равен произведению длины ребра
. Поэтому объем параллелепипеда равен произведению длины ребра  на площадь основания. С другой стороны, этот же объем равен
на площадь основания. С другой стороны, этот же объем равен  . Поэтому
. Поэтому  . Отсюда
. Отсюда  .
.
Задача 23. Пользуясь определением и свойствами  - тензора, доказать некоторые свойства смешанного произведения.
- тензора, доказать некоторые свойства смешанного произведения.
Решение. Смешанное произведение трех векторов  ,
,  ,
,  с помощью
с помощью  - тензора записывается так:
- тензора записывается так:
 (155)
(155)
а) Докажем, что если векторы  ,
,  ,
,  компланарны, то их смешанное произведение равно нулю. Компланарные векторы лежат в одной плоскости. Но три вектора, лежащие в одной плоскости, обязательно будут линейно зависимыми. Это означает, что один из них представляет собой линейную комбинацию двух других. Например,
компланарны, то их смешанное произведение равно нулю. Компланарные векторы лежат в одной плоскости. Но три вектора, лежащие в одной плоскости, обязательно будут линейно зависимыми. Это означает, что один из них представляет собой линейную комбинацию двух других. Например,  или в координатах:
или в координатах: 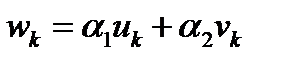 . Смешанное произведение таких векторов будет равно:
. Смешанное произведение таких векторов будет равно:

Расписывая каждое слагаемое подробно, так же, как в задаче 22а, легко показать, что оба они равны нулю, т.е. равно нулю само смешанное произведение.
б) Докажем, что если переставить местами два сомножителя в смешанном произведении, то оно меняет знак:  .
.
Поскольку здесь все индексы немые и их можно обозначить любыми буквами, то мы произвели замену индексов так:  ,
,  .
.
в) Докажем, что при круговой перестановке сомножителей смешанное произведение не меняется:
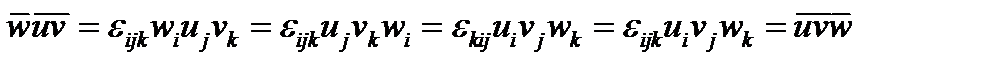 .
.
Здесь мы произвели замену немых индексов так:  ,
,  ,
, 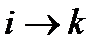 .
.
Задача 24. Доказать, что двойное векторное произведение трех векторов  можно представить в виде
можно представить в виде
 (156).
(156).
Решение: Пользуясь  - тензором, нетрудно получить, что:
- тензором, нетрудно получить, что:

Задача 25. Показать, что  является бивектором и построить эквивалентный ему аксиальный вектор.
является бивектором и построить эквивалентный ему аксиальный вектор.
Решение. Как было определено в параграфе 19, бивектором называется антисимметричный тензор 2-ого ранга. Докажем вначале, что величины  образуют тензор 2-ого ранга. Ограничившись только правыми системами координат, получим, что при преобразовании координат:
образуют тензор 2-ого ранга. Ограничившись только правыми системами координат, получим, что при преобразовании координат:
 ,
,
т.е. величины  действительно преобразуются как компоненты тензора 2-ого ранга. Докажем теперь антисимметричность тензора
действительно преобразуются как компоненты тензора 2-ого ранга. Докажем теперь антисимметричность тензора  :
:  .
.
Как было показано в параграфе 19 (формула (143)), вектор, эквивалентный бивектору, равен  . В данном случае:
. В данном случае:
 .
.
Мы воспользовались здесь второй формулой (119). Таким образом, вектор, эквивалентный бивектору, совпадает с вектором  .
.
Задача 26. Показать, что вектор, двойственный произвольному тензору  , зависит только от его антисимметричной части
, зависит только от его антисимметричной части  .
.
Решение. Вектор, двойственный произвольному тензору второго ранга  , был определен в параграфе 20 формулой (145):
, был определен в параграфе 20 формулой (145):  .
.
Разложив тензор  на симметричную
на симметричную  и антисимметричную
и антисимметричную  части, получим:
части, получим:
 , (157)
, (157)
где 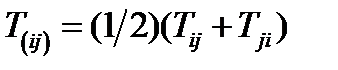 ,
,  .
.
Покажем, что первое слагаемое в (157), соответствующее симметричной части тензора  , равно нулю:
, равно нулю:  . Поскольку индексы
. Поскольку индексы  – немые и их можно обозначить любыми буквами, то сделаем замену этих индексов:
– немые и их можно обозначить любыми буквами, то сделаем замену этих индексов:  . Тогда:
. Тогда: 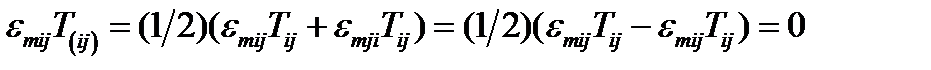 , а это означает, что двойственный вектор
, а это означает, что двойственный вектор  от симметричной части тензора
от симметричной части тензора  не зависит.
не зависит.
|
из
5.00
|
Обсуждение в статье: Векторное произведение как антисимметричный тензор |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

