 |
Главная |
Степени тензоров второго ранга
|
из
5.00
|
Уравнение Гамильтона-Кэли.
Приведение симметричного тензора 2-го ранга к главным осям позволяет очень просто записать степени этого тензора. В параграфе 16 был определен квадрат тензора  как тензор
как тензор  , куб – как
, куб – как  и т.д. Легко показать, что из симметрии тензора
и т.д. Легко показать, что из симметрии тензора  следует симметрия всех его степеней (Задача 32). Если матрица симметричного тензора относительно системы главных осей имеет диагональный вид (177), то квадрат тензора в той же системе равен
следует симметрия всех его степеней (Задача 32). Если матрица симметричного тензора относительно системы главных осей имеет диагональный вид (177), то квадрат тензора в той же системе равен
 (185)
(185)
Аналогично для всех других степеней, и в общем виде:
 (186)
(186)
Сравнение (186) и (177) показывает, что тензор  и все его целые степени имеют одни и те же главные оси.
и все его целые степени имеют одни и те же главные оси.
Все главные значения удовлетворяют характеристическому уравнению (163), а матрица тензора  имеет диагональный вид (186). Из этого следует, что сам тензор
имеет диагональный вид (186). Из этого следует, что сам тензор  будет удовлетворять уравнению (163). Таким образом, получаем:
будет удовлетворять уравнению (163). Таким образом, получаем:
 , (187)
, (187)
где 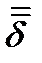 – единичный тензор. Уравнение (187) называется уравнением Гамильтона-Кэли. Из него получаем:
– единичный тензор. Уравнение (187) называется уравнением Гамильтона-Кэли. Из него получаем:
 (188)
(188)
Умножим обе части на тензор  со свертыванием по одной паре индексов, т.е. способом, описанным в пункте 5 параграфа 16, которым получаются степени тензора
со свертыванием по одной паре индексов, т.е. способом, описанным в пункте 5 параграфа 16, которым получаются степени тензора  :
:
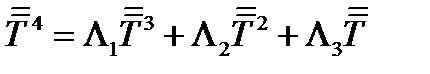 .
.
Подставив сюда (188), после преобразований получим:
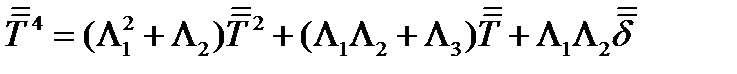 (189)
(189)
Продолжая действовать таким же образом, можно получить более высокие степени тензора  в виде линейных комбинаций тензоров
в виде линейных комбинаций тензоров  ,
,  ,
,  . Коэффициенты этих линейных комбинаций представляют собой многочлены относительно инвариантов
. Коэффициенты этих линейных комбинаций представляют собой многочлены относительно инвариантов  .
.
Круги Мора.
Часто случается, что мы хотим преобразовать компоненты симметричного тензора 2-го ранга от одной системы координат к другой, получающейся из первой простым поворотом вокруг одной из осей. Компоненты тензора в новой системе можно найти графически с помощью построения Мора.
Предположим, что новая система координат получается из старой поворотом вокруг оси  на угол
на угол  против часовой стрелки. Этот случай был рассмотрен в задаче 2 параграфа 8 (см. Рис. 6). Матрица перехода
против часовой стрелки. Этот случай был рассмотрен в задаче 2 параграфа 8 (см. Рис. 6). Матрица перехода  была определена формулой (53). Воспроизведём её:
была определена формулой (53). Воспроизведём её:
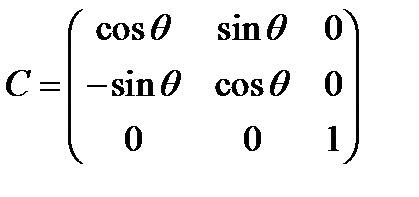 (190)
(190)
Пусть старые оси координат  – это главные оси тензора
– это главные оси тензора 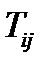 . Это значит, что в старой системе матрица тензора диагональна (см. формулу (177)). Компоненты тензора в новой системе
. Это значит, что в старой системе матрица тензора диагональна (см. формулу (177)). Компоненты тензора в новой системе  определяются по уже известной нам формуле:
определяются по уже известной нам формуле:
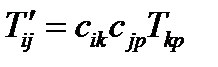 (192)
(192)
Имея в виду формулу (177), получим:
 (193)
(193)
Учитывая, что матрица перехода определена формулой (190), имеем:
 (194)
(194)
т.е. из всех компонент тензора в новой системе отличны от нуля только четыре:  (195)
(195)
где  ,
,  ,
,
 .
.
Преобразуем эти формулы к виду:
 (196)
(196)

|

|
|

|

|
|

|

|

|
| Рис. 12а) |

|
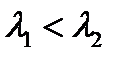 . Отметим на оси абсцисс точки
. Отметим на оси абсцисс точки  и
и  , и на отрезке между ними как на диаметре построим окружность.
, и на отрезке между ними как на диаметре построим окружность.

|
 . Центр окружности – точка
. Центр окружности – точка 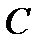 – имеет абсциссу, равную
– имеет абсциссу, равную 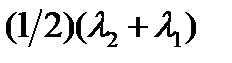 . Построим радиус
. Построим радиус  так, чтобы угол, образуемый им с осью абсцисс, был равен
так, чтобы угол, образуемый им с осью абсцисс, был равен  и откладывался против часовой стрелки. Найдем координаты точки
и откладывался против часовой стрелки. Найдем координаты точки  . Абсцисса будет равна:
. Абсцисса будет равна:  , а ордината
, а ордината 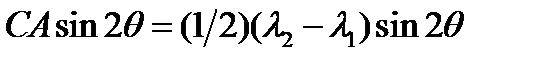 .
.
Сравнивая с формулами (196), видим, что координаты точки  равны компонентам тензора
равны компонентам тензора  и
и 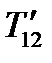 , т.е.
, т.е. 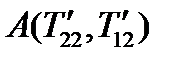 . Продолжим радиус
. Продолжим радиус  до точки
до точки  и получим, что абсцисса точки
и получим, что абсцисса точки  равна:
равна:
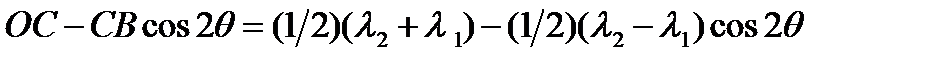 , т.е. координаты точки
, т.е. координаты точки  :
:  .
.
Когда ось  на рис. 6 поворачивается против часовой стрелки до совпадения с осью
на рис. 6 поворачивается против часовой стрелки до совпадения с осью  , точка
, точка  на рис. 12а движется вдоль верхней половины окружности от положения
на рис. 12а движется вдоль верхней половины окружности от положения  до положения
до положения  . Компоненты тензора
. Компоненты тензора 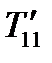 и
и  всегда имеют промежуточное значение между
всегда имеют промежуточное значение между  и
и  , и достигают экстремальных значений, когда точка
, и достигают экстремальных значений, когда точка  находится в положениях
находится в положениях  или
или  , т.е. когда новые оси
, т.е. когда новые оси  совпадают с главными осями. Легко видеть также, что сумма
совпадают с главными осями. Легко видеть также, что сумма 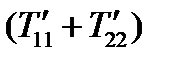 имеет неизменное значение при любом положении осей координат. Следовательно,
имеет неизменное значение при любом положении осей координат. Следовательно, 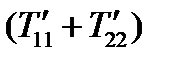 является инвариантом этого преобразования:
является инвариантом этого преобразования:  .
.
Компонента  достигает наибольшего значения, равного
достигает наибольшего значения, равного  , когда
, когда  , или
, или  . Когда ось
. Когда ось  вращается в обратном направлении, то точка
вращается в обратном направлении, то точка  тоже движется в обратном направлении. Компонента
тоже движется в обратном направлении. Компонента  отрицательна, когда точка
отрицательна, когда точка  находится на нижней полуокружности.
находится на нижней полуокружности.

|
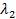
|
| Рис. 12в) |
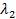
|

|

|

|
| Рис. 12б) |
 и
и  положительны, но все построение остается справедливым и в том случае, когда оба главных значения
положительны, но все построение остается справедливым и в том случае, когда оба главных значения  и
и  отрицательны, как показано на рис. 12б, или они имеют разные знаки, как на рис. 12в.
отрицательны, как показано на рис. 12б, или они имеют разные знаки, как на рис. 12в.

|
 . Рассмотрим теперь обратную задачу. Пусть известны компоненты тензора
. Рассмотрим теперь обратную задачу. Пусть известны компоненты тензора 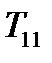 ,
,  ,
,  . Необходимо найти главные значения
. Необходимо найти главные значения  и
и  . Отмечаем на плоскости две точки:
. Отмечаем на плоскости две точки:  и
и  . На отрезке
. На отрезке  , как на диаметре, строим окружность. Точки пересечения окружности с осью абсцисс и определяют главные значения.
, как на диаметре, строим окружность. Точки пересечения окружности с осью абсцисс и определяют главные значения.
На практике построение окружности Мора полезно, главным образом, как быстрый способ вывода формул. Из выражений (196) можно найти главные значения  и
и  . Но пользуясь окружностью Мора, это можно сделать гораздо быстрее. Из рис. 12а видно, что
. Но пользуясь окружностью Мора, это можно сделать гораздо быстрее. Из рис. 12а видно, что
 ,
,  (197)
(197)
Отрезок  определяет абсциссу центра окружности Мора. Ее легко найти, зная координаты точек
определяет абсциссу центра окружности Мора. Ее легко найти, зная координаты точек  и
и 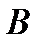 :
:
 (198)
(198)
Отрезок  , как и
, как и  , равен радиусу окружности. Его можно найти опять-таки, зная координаты точек
, равен радиусу окружности. Его можно найти опять-таки, зная координаты точек  и
и 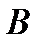 :
:
 (199)
(199)
Тогда: 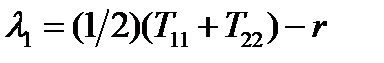 ,
,  (200)
(200)
Угол поворота  точки легко определить из рис. 12:
точки легко определить из рис. 12:
 (201)
(201)
При построении рис. 12а-в мы предполагали, что вращение системы координат происходит вокруг оси  , и что
, и что  . На практике часто приходится применять это построение для случаев, когда порядок осей не соответствует рассмотренной схеме. Поэтому поступают следующим образом. Из двух главных компонент, участвующих в преобразовании, выбирается наибольшая и соответствующее ей главное направление принимается за ось
. На практике часто приходится применять это построение для случаев, когда порядок осей не соответствует рассмотренной схеме. Поэтому поступают следующим образом. Из двух главных компонент, участвующих в преобразовании, выбирается наибольшая и соответствующее ей главное направление принимается за ось  . Вдоль главного направления, соответствующего меньшей компоненте, направляется ось
. Вдоль главного направления, соответствующего меньшей компоненте, направляется ось 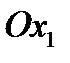 . Затем вводятся соответствующие обозначения осей на чертежах рис. 12а-в.
. Затем вводятся соответствующие обозначения осей на чертежах рис. 12а-в.
|
из
5.00
|
Обсуждение в статье: Степени тензоров второго ранга |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

