Теоремы умножения и сложения вероятностей

Условная вероятность. Правило умножения вероятностей

Условной вероятностью события A по отношению к событию B называется вероятность события A, найденная при условии, что событие B произошло. Обозначается символом .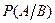

События A и B называются независимыми, если появление одного из них не меняет вероятность появления другого, т. е. если

, .

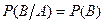Теорема (правило) умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого, найденную в предположении, что первое событие произошло, т.е.

или (4)

Теорема умножения вероятностей для нескольких событий.Вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности остальных событий, вычисленные в предположении, что все предыдущие события произошли, т. е.

. (5)

Для независимых событий и правило умножения вероятностей принимает вид:

(6)

Эта формула часто используется в качестве определения независимых событий.

События называются независимыми (или независимыми в совокупности), если вероятность любого из них не меняется от того, что произошло одно или несколько других событий, т. е.

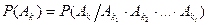, где .

В случае n независимыхсобытий имеем

, (7)

т.е. вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий.

События называются попарно - независимыми, если любые два события и ( ) из этого набора независимы.

Независимые события являются попарно – независимыми. Обратное, вообще говоря, неверно.

Вероятность суммы совместных событий

Вероятность суммы конечного числа попарно несовместных событийопределяется аксиомой 3(аксиомой сложения вероятностей).

При решении ряда задач требуется найти вероятность суммы двух или нескольких совместных событий, т.е. вероятность появления хотя бы одного из этих событий. В этом случае аксиома сложения вероятностей не применима.

Теорема (правило) сложения вероятностей.Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения, т. е.

(8)

В случае трех и более совместных событий соответствующая формула для вероятности суммы событий весьма громоздка, проще перейти к противоположному событию и затем воспользоваться равенством . Тогда

, (9)

т. е. вероятность суммы нескольких совместных событий 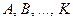равна разности между единицей и вероятностью произведения противоположных событий .

Если при этом события независимые, то

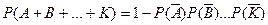(10)

Решение задач

Пример 1. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4 % всей продукции является браком, а 75 % небракованных изделий удовлетворяют требованиям первого сорта.

Решение.Пусть событие A={выбранное изделие небракованное}, событие B={небракованное изделие удовлетворяет требованиям первого сорта}, событие C={выбранное наудачу изделие первосортное}. Событие C предоставляет собой произведение событий A и B: C=AB. По условию , 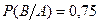. Тогда по теореме умножения вероятностей (см. 2.1) искомая вероятность .

Пример 2. В первом ящике 2 белых и 10 красных шаров; во втором ящике 8 белых и 4 красных шара. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые?

Решение.В данном случае речь идет о совмещении событий A и B, где событие A={появление белого шара из первого ящика}, событие B={появление белого шара из второго ящика}. При этом A и B – независимые события. Имеем , . По теореме умножения для независимых событий (см. (6)) находим .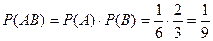

Пример 3. На 100 лотерейных билетов приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному билету, если приобретено: а) 2 билета; б) 4 билета?

Решение.Пусть событие ={выигрыш по 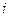-му билету}, 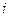=1, 2, 3, 4. События - совместные, но зависимые.

а) По формулам (8) и (4) вероятность выигрыша хотя бы по одному из двух билетов

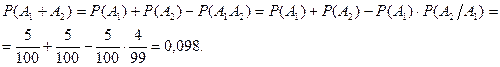
б) по формулам (9) и (5) вероятность выигрыша хотя бы по одному из четырех билетов

Пример 4.Произведено три выстрела по цели из орудия. Вероятность попадания при первом выстреле равна 0,75, при втором – 0,8, при третьем – 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.

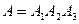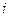Решение.а) Пусть событие A состоит в том, что будет три попадания в цель. Событие A представляет собой произведение трех событий: , где - попадание в цель при -м выстреле, 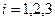. События - независимые. По теореме умножения для независимых событий (см. (7)) .

б) Пусть событие B состоит в том, что будет хотя бы одно попадание в цель при трех выстрелах (т.е. не менее одного попадания в цель). Событие - сложное событие. События - совместные, а потому использовать аксиому сложения для вычисления вероятности события B нельзя. Представим событие B в виде суммы несовместных событий (вариантов):

.

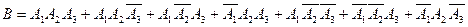По теореме умножения для независимых событий можно найти вероятность каждого варианта и все эти вероятности сложить в соответствии с аксиомой сложения. Однако такой путь решения задачи слишком сложен. Целесообразнее от события B перейти к противоположному событию ={нет ни одного попадания в цель при трех выстрелах}. Учитывая, что событие , по теореме умножения для независимых событий (см. (7)), найдем , откуда .

На этом примере проиллюстрирован принцип целесообразности применения противоположных событий в теории вероятностей.

Пример 5. Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,3, второй – 0,4, третий -0,5. По условиям приема события, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.

Решение.Пусть событие ={принят корреспондентом 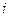-й вызов}, 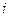=1, 2, 3. События совместные и независимые. По условию ; ; . Событие B={корреспондент вообще услышит вызов}: . Найдем вероятность события B. Для этого от события B перейдем к противоположному событию {корреспондент не услышит вызов}: 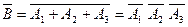, воспользовавшись формулой (9), найдем:

Пример 6.Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,9, третий – 0,8. Найти вероятность того, что студентом будут сданы: а) только 2-й экзамен; б) только один экзамен; в) три экзамена; г) по крайней мере два экзамена; д) хотя бы один экзамен.

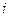Решение. а) Обозначим события: = {студент сдаст -й экзамен}, 1,2,3; B = {студент сдаст только 2-й экзамен из трех}. Очевидно, что событие B представляет собой совместное наступление трех событий, состоящих в том, что студент сдаст 2-й экзамен и не сдаст 1-й и 3-й экзамены, т.е. . Учитывая, что события независимы, получим .

б) Пусть событие C = {студент сдаст один экзамен из трех}. Очевидно, что событие C можно представить в виде суммы трех несовместных событий: .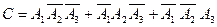

По аксиоме сложения и теореме умножения для независимых событий .

в) Пусть событие E = {студент сдаст все три экзамена}, т.е. . Тогда по формуле (7) .

г) Пусть событие F = {студент сдаст, по крайней мере, два экзамена} (т.е. хотя бы два экзамена или не менее двух экзаменов). Ясно, что событие F означает сдачу любых двух экзаменов из трех, либо всех трех экзаменов. Представим событие F в виде суммы несовместных событий: .

Тогда по аксиоме сложения и теореме умножения для независимых событий найдем .

д) Пусть событие K – студент сдал хотя бы один экзамен (т.е. не менее одного экзамена). От прямого события K перейдем к противоположному событию и воспользуемся формулой (2.7). Тогда

т.е. сдача хотя бы одного экзамена из трех является событием практически достоверным.