Непосредственный подсчет вероятностей

Рассмотрим несколько примеров вычисления вероятностей событий, пользуясь классическим определением вероятности. Приводимые ниже примеры носят исключительно иллюстративный характер.

Пример 1.В первом ящике находятся шары с номерами от 1 до 5, а во втором – с номерами от 6 до 10. Из каждого ящика вынули по одному шару. Какова вероятность того, что сумма номеров вынутых шаров: а) не меньше 7; б) равна 11; в) не больше 11?

Решение.а) Пусть A – событие, состоящее в том, что сумма номеров вынутых шаров не меньше 7 (т.е. больше или равна 7).

После вынимания из каждого ящика по одному шару возможны следующие исходы: (1,6), (1,7), (1,8), (1,9), (1,10), (2,6), (2,7), (2,8), (2,9), (2,10), (3,6), (3,7), (3,8), (3,9), (3,10), (4,6), (4,7), (4,8), (4,9), (4,10), (5,6), (5,7), (5,8), (5,9), (5,10).

Число всех равновозможных случаев (исходов) . Очевидно, что число случаев (исходов), благоприятствующих наступлению события A, равно m=25. Тогда по формуле (1) . Событие A – достоверное.

б) Исходами, благоприятствующими наступлению события B={сумма номеров вынутых шаров равна 11}, являются (5,6), (4,7), (3,8), (2,9), (1,10). Число таких случаев m=5. Число всех равновозможных случаев (см. пункт a). Поэтому .

в) Число всех случаев . Исходами, благоприятствующими наступлению события C={сумма номеров вынутых шаров не больше 11 (т.е. меньше или равна 11)}, являются (1,6), (1,7), (1,8), (1,9), (1,10), (2,6), (2,7), (2,8), (2,9), (3,6), (3,7), (3,8), (4,6), (4,7), (5,6). Число таких случаев равно . Следовательно, .

Пример 2.Числа 1, 2, 3, 4, 5 написаны на пяти карточках. Наугад последовательно выбираются три карточки, и вынутые таким образом цифры ставятся слева направо. Найти вероятность того, что полученное при этом трехзначное число будет четным.

Решение. Пусть событие A={получение четного трехзначного числа}. Различные комбинации трех цифр из имеющихся пяти представляют собой размещения, так как они могут отличаться как составом входящих цифр, так и порядком их следования (или и тем и другим), т. е. общее число всех случаев , из которых событию A благоприятствует случаев (число будет четным, если оно оканчивается либо на 2, либо на 4). По формуле (1) .

Пример 3. (задача о выборке). В партии из 50 деталей 5 нестандартных. Определить вероятность того, что среди выбранных наудачу для проверки 6 деталей 2 окажутся нестандартными.

Решение. Пусть событие A={из 6 выбранных наудачу для проверки деталей две - нестандартные}. Общее число всех случаев выбора 6 деталей из 50 равно , так как комбинации из 50 деталей по 6 представляют собой сочетания, ибо они отличаются только составом деталей. Определим число случаев, благоприятствующих событию A. Число способов выбрать 2 нестандартные детали из 5, находящихся в партии, равно . Каждому такому выбору соответствует 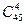способов выбора 4 стандартных деталей из 45 стандартных деталей в партии. Следовательно, по правилу произведения число случаев, благоприятствующих событию A, равно: . Таким образом, .

Пример 4. Из колоды карт (36 карт) наудачу вынимаются 3 карты. Найти вероятность того, что среди них окажется хотя бы одна “дама”.

Решение. Обозначим интересующее нас событие буквой A. Событие A можно представить в виде суммы трех несовместных событий: , где событие - появление одной “дамы”, - появление двух “дам”, - появление трех “дам”. Проводя рассуждения, аналогичные тем, которые были при решении предыдущей задачи, найдем, что число случаев, благоприятствующих событиям равно соответственно , , . Так как число всевозможных случаев выбрать 3 карты из 36 равно , то ; ; .

В силу аксиомы сложения .

Этот пример можно решить и иным способом.

Пусть событие , противоположное событию A, состоит в том, что среди вынутых трех карт не окажется ни одной “дамы”. Очевидно, что число случаев, благоприятствующих событию , равно и, следовательно, .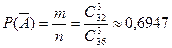

Тогда искомая вероятность .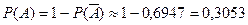

Пример 5.В урне 3 белых, 6 красных и 5 синих шаров. Из нее наудачу вынимают 3 шара. Какова вероятность того, что: a) все они одного цвета; б) все они разных цветов; в) среди них 1 белый и 2 синих шара.

Решение.Сначала заметим, что число способов вынуть 3 шара из 14, имеющихся в урне, равно .

а) Пусть событие A состоит в том, что три шара, вынутых из урны, одного цвета (т.е. три шара либо белые, либо красные, либо синие). Выбрать 3 белых шара из 3 можно способами; 3 красных из имеющихся 6 можно выбрать способами; 3 синих из 5 синих - способами. По правилу суммы общее число m случаев, благоприятствующих событию A, равно . Отсюда .

б) Пусть событие B состоит в том, что три вынутых из урны шара разных цветов. По правилу произведения, найдем, что число m случаев, благоприятствующих событию B, равно . Поэтому .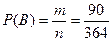

в) Пусть C – событие, состоящее в том, что из трех вынутых шаров, 1 белый и 2 синих. Выбрать 1 белый шар из имеющихся в урне 3 белых шаров можно способами, а 2 синих из имеющихся 5 синих - способами. Тогда по правилу произведения имеем: . Следовательно, .

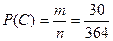Пример 6.Наудачу взятый телефонный номер состоит из 5 цифр. Как велика вероятность, что в нем: 1) все цифры различные; 2) все цифры нечетные?

Решение. 1) Пусть событие A состоит в том, что все цифры пятизначного телефонного номера различны. Так как на каждом из пяти мест в пятизначном номере может стоять любая из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то число всех различных пятизначных номеров (все они могут быть перенумерованы следующим образом: номер 00000 – 1-й, 00001 – 2-й, 00002 – 3-й, …, 99998 - 99999-й и, наконец, 99999 – 100 000 –й). Номера, у которых все цифры различные, есть размещение из 10 элементов по 5. Поэтому, число случаев, благоприятствующих событию A, и искомая вероятность .

2) Пусть событие B – все цифры пятизначного номера нечетные. Поскольку из 5 нечетных цифр (1, 3, 5, 7, 9) можно образовать различных пятизначных номеров, то число случаев, благоприятствующих событию B, m = . Учитывая, что число всех равновозможных случаев , найдем .