Краевые, граничные условия. Задачи Дирихле и Неймана. Функция Грина задач электростатики

 

Уравнение Пуассона иногда решают в граничных условиях. Задаются краевые граничные условия типа Дирихле или типа Неймана.

В задаче Дирихле задаётся потенциал:

- краевое условие Дирихле.

В задаче Неймана задается :

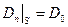- краевое условие Неймана.

и - заданные нами функции.

Они задаются для уравнения Пуассона в электростатике.

В случае изотропных сред:

В случае задачи Неймана для изотропных сред:

 

Общее решение уравнения Пуассона состоит из общего решения соответствующего однородного уравнения - и частного решения неоднородного -

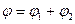
На лежит нагрузка удовлетворения граничным условиям, удовлетворяет однородным граничным условиям:

Рассмотрим . Далее будем писать без индекса, т.е. .

Введём некоторый интегральный оператор и

Если , то

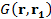- ядро интегрального оператора , т. е. 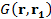- функция Грина.

Пусть - единичный оператор, т.е. , тогда:

-ядро единичного оператора, это и есть

Итак, на языке ядер выглядит следующим образом:

, есть функция Грина задач электростатики.

определяется характером граничных условий.

1. - частное решение, удовлетворяющее однородному граничному условию Дирихле.

тогда из того, что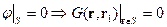

2. - граничное условие Неймана

В обоих случаях и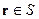

Для

 

 

Физический смысл функции Грина. Теорема взаимности в электростатике

 

Из равенства видно, что при помощи получаем:

т.е. точечный заряд источник потенциала - функции Грина.

Сравним левые части выражений:

Следовательно - потенциал, создаваемый в точке 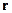порождённый точечным зарядом с .

, здесь - точка, где находится источник, а функция Грина является функцией источника.

Функция Грина – это потенциал в точке 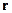, создаваемый зарядом , помещённым в точку . В этом заключается физический смысл функции Грина.

- потенциал, создаваемый в точке 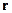элементарным зарядом , помещённым в точку . Значит

 

На языке функции Грина:

Смысл теоремы: Потенциал, создаваемый в точке 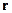точечным источником, помещённым в точку равен потенциалу, создаваемому в точке тем же точечным источником, помещённым в точку .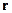

 

На языке операторов:

 

* - комплексное сопряжение

T- транспонирование

 

Факультатив

 

1 § 1. Тензоры и их свойства. Симметрия кристаллов

 

Запись преобразований тензора 2-го ранга при вращении.

Пусть у нас есть монокристалл определённого вещества. Существует набор преобразований, при которых его свойства инвариантны. Операции симметрии можно задать матрицами ортогональных преобразований

 

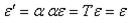
Оператор принадлежит к симметрическим операторам. Итак, условие инвариантности:

Для монокристалла орторомбической системы:

Оси выбираются к характерным направлениям в кристалле.

Для монокристаллов гексагональной системы:

Для кубической:

 

При решении кристаллофизических задач часто оказывается удобной не кристаллофизическая (декартова система координат, условленным образом ориентированная относительно кристаллографической системы), а какая-то другая декартова система координат, направления осей которой определяются геометрией данной задачи. Так как система декартовых координат полностью задается своим ортонормированным базисом, преобразование декартовых координат означает переход от одного ортонормированного базиса к другому.

Преобразование, при котором ортонормированный базис переходит в ортонормированный, называется ортогональным преобразованием.

Пусть старая система координат построена на базисе , а новая -на базисе . Разложение нового базиса по векторам старого определяется коэффициентами , которые образуют матрицу ортогонального преобразования:

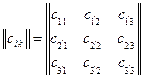
Она также называется матрицей косинусов, поскольку каждый ее элемент равен косинусу угла между соответствующими координатными осями. Ортогональные преобразования обладают тем свойством, что квадрат определителя их матрицы равен единице [4, с. 135].

Примерами матриц ортогональных преобразований могут выступать:

матрица вращения вокруг оси Z:

матрица отражения относительно плоскости XY:

Для описания свойств кристалла введем материальные тензоры. Материальными называются тензоры, которые описывают свойства кристалла.

Пусть с кристаллом связана какая-либо декартова система координат. Набор компонент материального тензора относительно этой системы координат численно характеризует соответствующее свойство. Подвергнем координатную систему какому-либо ортогональному преобразованию. Компоненты материального тензора относительно новой системы, вообще говоря, не равны одноименным его компонентам относительно старой системы. Однако если данное преобразование входит в группу симметрии кристалла, то компоненты материального тензора относительно новой системы совпадают с его компонентами относительно старой. Следовательно, материальный тензор кристалла инвариантен относительно всех преобразований симметрии этого кристалла.

Пусть - материальный тензор, а - матрица преобразования симметрии кристалла, свойства которого этот тензор описывает. В новой системе координат

причем компоненты тензора в новой системе должны совпадать с его компонентами в старой системе. Поэтому можно записать:

Отсюда получим:

и эти равенств должны выполняться, если - матрица преобразования симметрии.