|
Главная |
Основные теоремы о направленности антенн
|
из
5.00
|
ТЕОРЕМА СЛОЖЕНИЯ – является прямым следствием принципа суперпозиции и утверждает, что если антенна имеет амплитудно-фазовое распределение колебательной скорости по ее поверхности F(s), равное сумме двух функций A(s) и B(s), то она создает в произвольной точке пространства такое же давление как и две антенны с распределениями A(s) и B(s). Т.е. поскольку характеристика направленности отражает распределение энергии в пространстве, то теорема сложения показывает, что в каждом направлении энергия от двух или нескольких источников суммируется, и общее распределение энергии в пространстве от нескольких источников можно заменить распределением от одного источника с определенным амплитудно-фазовым распределением. Для отыскания характеристики направленности антенну можно представить состоящей из двух или большего числа частей многими способами, причем для использования впоследствии теоремы сложения удобно делать это так, чтобы фазовые центры частей антенны совпадали, иначе задача определения характеристики направленности усложняется необходимостью сложения комплексных величин.
ТЕОРЕМА СМЕЩЕНИЯ – теорема, используемая при расчетах характеристики направленности антенны в заданной плоскости. В соответствии с теоремой характеристика направленности антенны, лежащей в бесконечном экране, в некоторой плоскости, перпендикулярной экрану, равна характеристике направленности антенны, являющейся проекцией рассматриваемой антенны на плоскость. При проецировании антенны на плоскость производительность участка проецируемой антенны должна быть равна производительности участка исходной антенны.
ТЕОРЕМА УМНОЖЕНИЯ – теорема, используемая при расчетах характеристик направленности антенн, состоящих из элементов конечных размеров, групп элементов и непрерывных антенн, образованных путем параллельного переноса некоторой кривой вдоль образующей. Согласно теореме умножения характеристика направленности антенны, состоящей из одинаковых и одинаково ориентированных в пространстве элементов, характеристики направленности которых также одинаковы и одинаково ориентированы в пространстве, равна произведению характеристик направленности элемента антенны и характеристики направленности гипотетической антенны, состоящей из точечных элементов, расположенных в фазовых центрах реальных элементов и имеющих такое же амплитудно-фазовое распределение, что и реальные элементы. В формулировке теоремы под элементом можно принимать группу элементом и применять теорему последовательно несколько раз. Из теоремы следует, что характеристика направленности непрерывной антенны, полученной путем параллельного переноса некоторой кривой вдоль направляющей, равна произведению характеристик направленности этой кривой и направляющей.
ФАЗОВЫЙ ЦЕНТР АНТЕННЫ– характеристики направленности некоторых типов антенн отличаются одним интересным свойством, заключающемся в том, при фиксированном положении начала координат аргумент характеристики направленности (фазовая характеристика направленности) либо вообще не зависит от направления в пространстве, либо при плавном изменении положения в пространстве точки наблюдения меняет свое значение на p.В таких случаях говорят, что антенна имеет фазовый центр, совпадающий с началом координат. Наличие в антенне фазового центра свидетельствует о том, что фронт волны относительно выбранной системы координат сферический. В случае отсутствия фазового центра в рассмотрение вводят некоторый его эквивалент, например, частичный фазовый центр, эквивалентный фазовый центр и др. Антенны обладающие геометрической симметрией имеют фазовый центр.
Задача №3

|
| Рис. 10. Антенная решетка |
Антенна представляет собой решетку, набранную из антенн в виде отрезков прямых размером l. Расстояние между фазовыми центрами равно d.Вид антенны показан на рис.10. В результате решения необходимо:
1. Получить выражение, описывающее характеристику направленности такой антенны в плоскости параллельной отрезку прямой (параллельной оси х).
2. Определить размер l, при котором первый ноль характеристики направленности отрезка прямой попадает на первый дополнительный максимум, равный основному максимуму характеристики направленности гипотетической антенны, составленной из точечных элементов, расположенных в фазовых центрах реальных преобразователей.
3. Построить характеристику направленности антенны, полученной по п.2, определить ее параметры.
4. Определить коэффициент осевой концентрации такой антенны методом графического интегрирования.
5. Сравнить коэффициент осевой концентрации, полученный в п.3 с коэффициентом осевой концентрации, рассчитанным по формуле.
Решение
1.Антенна представляет собой решетку, состоящую из трех одинаковых, одинаково ориентированных в пространстве антенн в виде отрезка прямой. По теореме умножения характеристика направленности антенны, состоящей из n одинаковых, одинаково ориентированных в пространстве антенн равна характеристике направленности одной из составляющих ее антенн, умноженной на ХН гипотетической антенны, состоящей из точечных антенн, находящихся в фазовых центрах реальных антенн. Таким образом, ХН рассматриваемой антенны равна произведению ХН антенны в виде отрезка прямой и ХН антенны, представляющей собой эквидистантную антенную решетку с равномерным амплитудным распределением, состоящую из 3-х элементарных излучателей
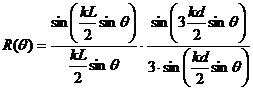
| (3.1) |
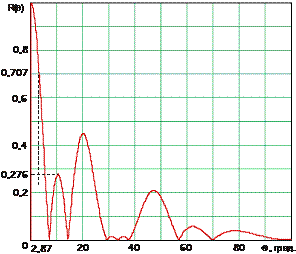
.Подставив заданные значения частоты f и размеров d и L, получим (см. рисунок 11)
|
| Рис. 11 |
Ширина ХН на уровне 0,7 равна 5,740.
Уровень первого бокового лепестка 27,6%.
- Чтобы ответить на второй вопрос, поставленный в задаче, необходимо приравнять выражения для определения направления нуля ХН отрезка прямой и направление максимума для эквидистантной антенной решетки
 отсюда
отсюда 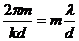 . l=d.
. l=d.
Т.е. при l=d первый нуль ХН отрезка прямой совпадет с первым дополнительным единичным максимумом гипотетической антенны.
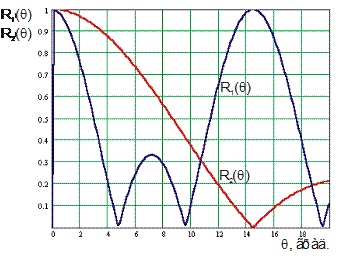
На рисунке 11 приведены модули характеристики направленности отрезка прямой и антенны в виде точечных источников, расположенных в фазовых центрах преобразователей антенны.
|
| Рис. 12 |
- Построим ХН антенны, у которой l=d . Для этого в выражение (3.1) подставим значение l=d. На рисунке 13 приведена характеристика направленности всей антенны.

|
| Рис. 13. ХН антенны при d=l |
Из рисунка следует, что уровень боковых лепестков такой антенны равен 22%, ее ширина на уровне –3дБ составляет приблизительно 40.
- Для определения коэффициента осевой концентрации (КОК) методом графического интегрирования построим ХН в декартовой системе координат в виде
 . Для этого в выражении (3.1) необходимо сделать замену переменных, принять
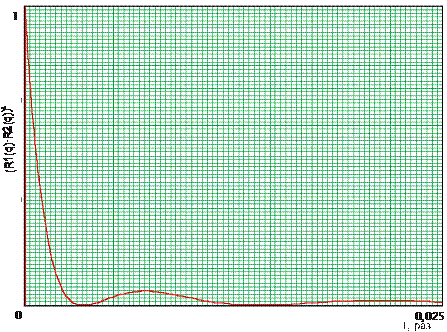
. Для этого в выражении (3.1) необходимо сделать замену переменных, принять  . При этом t меняется от 0 до 2. На рисунке 14 приведена часть графика для вычисления коэффициента осевой концентрации, по которому можно рассчитать площади под кривой и бланка, площадь которого соответствует площади под квадратом характеристики направленности ненаправленной антенны (точечного элемента.
. При этом t меняется от 0 до 2. На рисунке 14 приведена часть графика для вычисления коэффициента осевой концентрации, по которому можно рассчитать площади под кривой и бланка, площадь которого соответствует площади под квадратом характеристики направленности ненаправленной антенны (точечного элемента.
|
| Рис. 14 |
- Коэффициент осевой концентрации для такой антенны вычисляется по выражению
 .
.
Вычисление проводим с помощью прикладной программы MathCad, получаем

1.4. Влияние амплитудных распределений на характеристику направленности антенны
АМПЛИТУДНО-ФАЗОВОЕ РАСПРЕДЕЛЕНИЕ - в теории антенн вводится комплексный коэффициент возбуждения элементов антенны равный отношению нормальной составляющей колебательной скорости поверхности произвольного элемента антенны к нормальной составляющей колебательной скорости поверхности элемента антенны, принятого за опорный. Обычно за опорный элемент принимают лежащий в фазовом центре антенны. Модуль комплексного коэффициента возбуждения называется коэффициентом амплитудного распределения, а аргумент – коэффициентом фазового распределения. Амплитудное распределение вводится изменением напряжений возбуждения на элементах антенны, либо изменением чувствительности (или производительности) элементов антенны в режиме излучения, а в режиме приема возможно изменение коэффициентов усиления предварительных усилителей. Фазовое распределение вводится посредством введения задержек сигналов в каналах антенной системы, либо введением фазовых сдвигов в каналах, что приводит к изменению разности хода лучей в антенне. С помощью амплитудного распределения возможно управление параметрами характеристики направленности – уровнем бокового излучения, шириной характеристики направленности. Линейное фазовое распределение приводит к изменению положения акустического луча, формируемого антенной, в пространстве, а фазовое распределение другого типа может изменять форму характеристики направленности и ее положение, в том числе можно создавать фокусирующие системы на основе введения фазовых распределений.
ХАРАКТЕРИСТИКА НАПРАВЛЕННОСТИ АНТЕННЫ В ВИДЕ ОТРЕЗКА ПРЯМОЙ. Характеристика направленности антенны в виде отрезка прямой определится формулой

 - определяет амплитудное распределение по отрезку.
- определяет амплитудное распределение по отрезку.
Определим приближенное выражение для вычисления ширины характеристики направленности антенны в виде отрезка прямой большего по сравнению с длиной волны размера при произвольном амплитудном распределении  . Для этого совместим начало координат с центром тяжести антенны и представляя ее некоторой материальной линией имеющей распределение плотности соответствующее распределению
. Для этого совместим начало координат с центром тяжести антенны и представляя ее некоторой материальной линией имеющей распределение плотности соответствующее распределению  . При этом должно выполняться условие
. При этом должно выполняться условие  .
.
Разложим в выражении для 
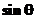 в ряд Тейлора вблизи точки
в ряд Тейлора вблизи точки  и ограничимся тремя первыми членами разложения
и ограничимся тремя первыми членами разложения
 ,
,
где  . Воспользуемся также разложением в степенной ряд экспоненциальной функцией
. Воспользуемся также разложением в степенной ряд экспоненциальной функцией  . В результате получим выражение для
. В результате получим выражение для  , состоящее из трех членов, один из которых обращается в нуль, вследствие выбора начала координат в центре тяжести прямой. Окончательно имеем
, состоящее из трех членов, один из которых обращается в нуль, вследствие выбора начала координат в центре тяжести прямой. Окончательно имеем
 .
.
Будем считать приближенно, что полная ширина характеристики направленности 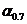 равна разности
равна разности 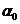 и
и  соответствующему значению ХН на уровне 0,707 и лежащему слева от
соответствующему значению ХН на уровне 0,707 и лежащему слева от 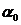 . Тогда
. Тогда  , при этом
, при этом  и второе слагаемое выражения равны 0,223. Откуда
и второе слагаемое выражения равны 0,223. Откуда
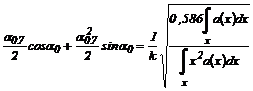 .
.
Рассмотрим частные случаи.
Пусть второе слагаемое в последнем выражении намного больше первого, тогда  и при малых
и при малых 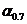 второе слагаемое не меньше чем на порядок отличается от первого при выполнении условия
второе слагаемое не меньше чем на порядок отличается от первого при выполнении условия
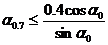
При выполнении этого условия
Если же антенна компенсирована в продольном направлении 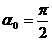 , то
, то
 .
.
Для случая равномерного распределения  можно получить следующие выражения
можно получить следующие выражения

 .
.
Рассматривая полученные выражения можно сделать следующие выводы:
- зависимость ширины характеристики направленности от волнового размера различна для разных углов компенсации.
- при выполнении условия (10.5) с увеличением наклона главного максимума характеристики направленности ширина ее возрастает пропорционально  .
.
Задача №4
Исследовать характеристику направленности антенны в виде отрезка прямой c размером L, лежащего в плоскости хоz, с различными амплитудными распределениями:  а(х) = сos х, сos2x, cos5x, для чего:
а(х) = сos х, сos2x, cos5x, для чего:
1. Построить вид амплитудного распределения.
2. Построить характеристику направленности такой антенны в плоскости параллельной отрезку при заданных значениях f, l, c при постоянных углах компенсации Θ0 = 00, 300, 450.
3. Исследовать зависимость ширины характеристики направленности от типа амплитудного распределения.
4. Построить зависимость амплитуды первого бокового лепестка R1 от типа амплитудного распределения (от значения показателя степени).
5. Построить ХН и исследовать ее ширину 2Θ0,7(l) и уровень боковых лепестков R1(l) в зависимости от размера антенны l (где l изменяется от 3λ до 10 λ), а также от длины волны 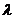 (т.е. 2Θ0,7(λ) и R1(λ) ) (λ изменяется от l/3 до l/10).
(т.е. 2Θ0,7(λ) и R1(λ) ) (λ изменяется от l/3 до l/10).
Решение.
1.Вид амплитудного распределения построим с помощью прикладной программы МathCad. При этом учтем, что первые нули функции cos((x) должны совпадать с концами антенны. Для этого аргумент функции cos необходимо разделить на l.
2.Построенный вид амплитудных распределений приведен на рис. 15.
3.Характеристику направленности антенны в виде отрезка прямой можно вычислить по выражению [1]
 .
.
На рисунке 16 приведены диаграммы направленности антенны для различных углов компенсации.
| ||
Рис. 16. ХН антенны при различных углах компенсации. Кривая 1 – угол компенсации 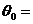 00, кривая 2 - 00, кривая 2 - 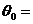 300, кривая 3 - 300, кривая 3 - 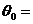 450 450
|
На рис. 17 приведены диаграммы направленности антенны в виде отрезка прямой с различным амплитудными распределением с углом компенсации  . Кривая 1 – равномерное амплитудное распределение, кривая 2 соответствует амплитудному распределению вида
. Кривая 1 – равномерное амплитудное распределение, кривая 2 соответствует амплитудному распределению вида  , кривая 3 -
, кривая 3 -  , кривая 4 -
, кривая 4 - 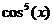 .
.

|
| Рис. 17. ХН антенны с различными амплитудными распределениями |
Полученные результаты показывают, что уровень боковых лепестков тем больше понижается чем выше показатель степени в амплитудном распределении, а ширина ХН при этом увеличивается.
4.На рис. 18 и 19 приведены зависимости ширины ХН и уровня боковых лепестков от показателя степени t изменения амплитудного распределения, соответственно.

|

|
| Рис.18. Зависимость ширины ХН от показателя степени амплитудного распределения | Рис.19. Зависимость уровня бокового лепестка от показателя степени амплитудного распределения |
5. Для построения зависимости ширины ХН и УБЛ от размеров антенны (l изменяется от 3λ до 10 λ) посчитаем ДН при различных значениях 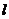 , оценим ширины ХН и УБЛ для каждого случая и построим искомые зависимости.
, оценим ширины ХН и УБЛ для каждого случая и построим искомые зависимости.

| 
|
| Рис. 19. Зависимость ширины ХН от изменения размеров антенны | Рис. 20. Зависимость уровня боковых лепестков от размеров антенны |
Примечание. Можно решить нелинейное уравнение вида 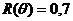 для различных значений размеров элементов антенны
для различных значений размеров элементов антенны 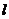 и найти таким способом ширину ХН.
и найти таким способом ширину ХН.
Используя предыдущий способ решения, оценить ширину ХН и УБЛ от длины излучаемой волны. Результаты оценки приведены на рис. 21, 22.

| 
|
| Рис. 21. Зависимость ширины ХН от длины волны | Рис. 22. Зависимость уровня боковых лепестков от длины волны |
Задача №5
В антенне, состоящей из 5 точечных элементов, расположенных на расстоянии d друг от друга, лежащей в плоскости xoz, задано амплитудное распределение в виде диаграмм (см. рис.24 )

| 
|
| a | б |
| Рис. 24 |
Рассчитать ХН антенны с заданными амплитудными распределениями. Определить ширину ХН, уровень боковых лепестков и коэффициент осевой концентрации, если антенна нагружена на воду, d=1cм. F=100 кГц.
Решение.
Для антенны состоящей из точечных источников характеристику направленности можно записать в виде
 .
.
а) Для амплитудного распределения, показанного на рисунке 24 б, предыдущее выражение можно записать в виде
 Построенная по этому выражению диаграмма направленности в плоскости параллельной прямой, вдоль которой располагаются элементы антенны показана на рисунке 25 кривой R1(Q).
Построенная по этому выражению диаграмма направленности в плоскости параллельной прямой, вдоль которой располагаются элементы антенны показана на рисунке 25 кривой R1(Q).
По кривой найдем ширина ХН равна 140, УБЛ=56%.
|
из
5.00
|
Обсуждение в статье: Основные теоремы о направленности антенн |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы