 |
Главная |
Несобственный интеграл.
|
из
5.00
|
Пусть f(x) определена и непрерывна на множестве от  и
и  . Тогда:
. Тогда:
1. Если  , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  называется сходящимся.
называется сходящимся.
2. Если не существует конечного  (
(  или
или  ), то интеграл
), то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся.
Пусть f(x) определена и непрерывна на множестве от  и
и  . Тогда:
. Тогда:
1. Если  , то используется обозначение
, то используется обозначение  и интеграл называется несобственным интегралом Римана первого рода. В этом случае
и интеграл называется несобственным интегралом Римана первого рода. В этом случае  называется сходящимся.
называется сходящимся.
2. Если не существует конечного  (
(  или
или  ), то интеграл
), то интеграл  называется расходящимся к
называется расходящимся к  , или просто расходящимся.
, или просто расходящимся.
Если функция f(x) определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:
 , где с — произвольное число.
, где с — произвольное число.


Признаки сходимости. Признаки сравнения.




Приложение определенного интеграла в физике и механике. Площадь плоской фигуры.
а) Площадь фигуры
Как уже отмечалось в лекции 19,  численно равен площади криволинейной трапеции, ограниченной кривой у = f(x) , прямыми х = а, х = b и отрезком [a, b] оси ОХ. При этом если f(x) £ 0 на [a, b], то интеграл следует взять со знаком минус.
численно равен площади криволинейной трапеции, ограниченной кривой у = f(x) , прямыми х = а, х = b и отрезком [a, b] оси ОХ. При этом если f(x) £ 0 на [a, b], то интеграл следует взять со знаком минус.
Если же на заданном отрезке функция у = f(x) меняет знак, то для вычисления площади фигуры, заключенной между графиком этой функции и осью ОХ, следует разбить отрезок на части, на каждой из которых функция сохраняет знак, и найти площадь каждой части фигуры. Искомая площадь в этом случае есть алгебраическая сумма интегралов по этим отрезкам, причем интегралы, соответствующие отрицательным значения функции, взяты в этой сумме со знаком «минус».
Если фигура ограничена двумя кривыми у = f1(x) и у = f2(x), f1(x)£f2(x), то, как следует из рис.9, ее площадь равна разности площадей криволинейных трапеций аВСb и аАDb, каждая из которых численно равна интегралу. Значит,
 .
.

|

Вычисление длины дуги плоской кривой
1 случай. Пусть в прямоугольных координатах на плоскости дана кривая  . Вычислим длину дуги кривой, заключенной между точками
. Вычислим длину дуги кривой, заключенной между точками  и
и  (рис. 12).
(рис. 12).

Возьмем на дуге  точки
точки  с абсциссами
с абсциссами  и проведем хорды
и проведем хорды  , длины которых обозначим соответственно
, длины которых обозначим соответственно  . Тогда получим ломанную
. Тогда получим ломанную  , вписанную в дугу
, вписанную в дугу  . Длина ломанной равна
. Длина ломанной равна
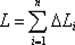 .
.
Определение. Длиной  дуги
дуги  называется тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю:
называется тот предел, к которому стремится длина вписанной ломанной, когда длина ее наибольшего звена стремится к нулю:
 .
.
Длина всей дуги  , заключенной между точками
, заключенной между точками  и
и  , вычисляется по формуле
, вычисляется по формуле
 .
.
В полярных .
Связь декартовых координат с полярными задается формулами

Известно, что длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле 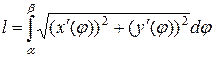 .
.
Вычислим производные координатных функций

Подставим их в подкоренное выражение и упростим его

Подставляя это выражение в формулу длины дуги кривой, заданной параметрическими уравнениями, получаем формулу длины дуги, заданной
в полярных координатах
 .
.
Параметрически:
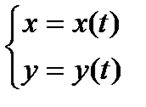 ,
,  ,
, 
 =
= 
Длина кривой заданной параметрически, выражается через определенный интеграл L= 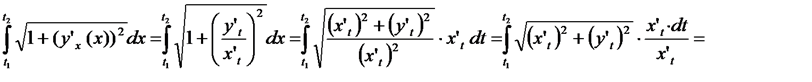
 .
.
|
из
5.00
|
Обсуждение в статье: Несобственный интеграл. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

