 |
Главная |
Замена переменной в неопр. интеграле.
|
из
5.00
|
Определение первообразной, неопределенный интеграл, свойства первообразной
Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство 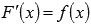 для любого х из заданного промежутка.
для любого х из заданного промежутка.
Теорема: Пусть - F1(x) и F2(x) - две первообразные для функции f(x) , тогдаF1(x)=F2(x)+C.
Док-во: рассмотримF1(x) - F2(x) и найдем ее производную F1’(x) -F2’(x) получилосьf(x)-f(x)=0 (любой xпринадлежащий промежутку)По следствию т Логранжа (если произв. функции на множестве равно 0, то эта ф. - const ) ->F1(x) - F2(x)=const=C, чтд т.е. F1(x) = F2(x)+С
Определениен. интеграла.Совокупность F(x)+C всех первообразных функции f(x) на множестве Х называется неопределенным интегралом и обозначается:
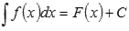
Выражение 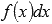 называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).
1. Производная от неопределенного интеграла равна подынтегральной функции.
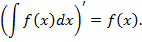
Доказательство. Непосредственно по определению неопределенного интеграла следует, что
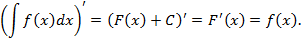
2. Дифференциал неопределенного интеграла равен подынтегральному выражению.
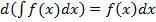 .
.
Доказательство.Из свойства 1 и по определению неопределенного интеграла и дифференциала, имеем
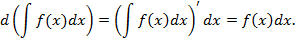
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного множителя.
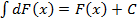 .
.
Доказательство. На основании свойства 2 и определения неопределенного интеграла, имеем
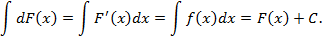
Следующие два свойства называются линейными свойствами неопределенного интеграла.
4. Постоянный множитель можно выносить за знак интеграла.
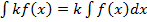 .
.
Доказательство. Введем новую функцию
 .
.
Возьмем производную этой функции и применяя свойство 1, получим
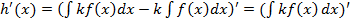 -
- 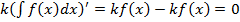 .
.
Из теоремы Лагранжа найдется такое число С,что 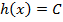 . Отсюда следует
. Отсюда следует
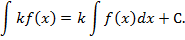
Замена переменной в неопр. интеграле.
Теорема.: Пусть функция x= φ(t) – строго монотонная и непрерывно дифференцируемая на некотором интервале функции φ(t). Если функция ƒ(x) интегрируема на соответствующем интервале измененийx, то имеет место равенство:
∫ ƒ(x)dx=∫ƒ(φ(t))·φ'(t)dt
Доказательство.
Определени1: Если функция ƒ(x) непрерывна на отрезке [a,b], то существует неопределенный интеграл∫ƒ(x)dx, а функция ƒ(x) в этом случае называется интегрируемой.
По определению1 неопределенного интеграла
∫ ƒ(x)dx=F(x) +C, причемF'(x) = ƒ(x)
Покажем, что функция F(φ(t)) является первообразной для функции: ƒ(φ(t))·φ'(t).
Для этого найдем (F(φ(t)))' = |по правилу дифференцирования сложной функции| =
= F'(φ(t))·φ'(t);
Но F'(φ(t)) = ƒ (φ(t)), тогда
(F(φ(t)))' = ƒ(φ(t))·φ'(t)
∫ƒ(φ(t))·φ'(t) dt = F(φ(t)) + C = F(x) + C = ∫ƒ(x) dx.
∫ƒ(x) dx = ∫ƒ(φ(t)) ·φ'(t) dt.
Пример 1.
Положим x – 1 = t ; тогда x = t + 1. Отсюда dx = dt.
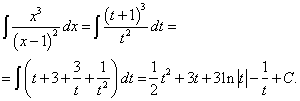
Возвращаясь к переменной x, окончательно получаем
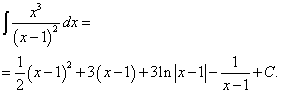
Пример 2.
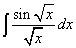 .
.
Решение. Положим 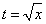 .Отсюда
.Отсюда
 .
.
По формуле (1)
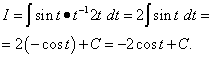 .
.
Возвращаясь к переменной x, окончательно получаем
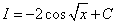
|
из
5.00
|
Обсуждение в статье: Замена переменной в неопр. интеграле. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

