 |
Главная |
Необходимое условие сходимости ряда.
|
из
5.00
|
Теорема: Если ряд 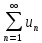 сходится, то его общий член
сходится, то его общий член 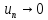 , т.е.
, т.е. 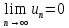 (1)
(1)
Доказательство: Если ряд 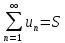 ,
, 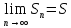 .Запишем:
.Запишем: 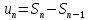 и найдем его предел
и найдем его предел 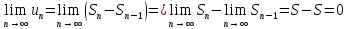 ч.т.д.
ч.т.д.
Если условие (1) не выполняется, то ряд расходится. Условие (1) не является достаточным условием сходимости ряда, т.е. из выполнения равенства 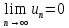 не обязательно вытекает сходимость ряда.
не обязательно вытекает сходимость ряда.
Пример.Гармоническим рядом называется ряд
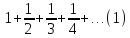
Для этого ряда 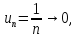 но этот ряд расходится, как показывает далее интегральный признак Коши.
но этот ряд расходится, как показывает далее интегральный признак Коши.


Расходимость гармонического ряда.


Теоремы сравнения для положительных рядов.
Если известно, что все члены ряда  имеют, начиная с некоторого номера, постоянный знак, то исследовать его сходимость проще, чем в общем случае. Это связано с простым критерием сходимости для таких рядов. Для простоты предположим, что все
имеют, начиная с некоторого номера, постоянный знак, то исследовать его сходимость проще, чем в общем случае. Это связано с простым критерием сходимости для таких рядов. Для простоты предположим, что все 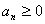 .
.
Теорема. (Критерий сходимости рядов с неотрицательными членами). Ряд 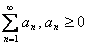 сходится
сходится 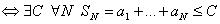 .
.
Доказательство.
 . Пусть
. Пусть 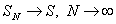 . Тогда
. Тогда 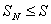 при всех
при всех 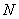 .
.
 . Пусть
. Пусть 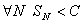 .Поскольку
.Поскольку 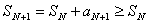 , последовательность
, последовательность  возрастает и, по условию, ограничена. Следовательно, по теореме Вейерштрасса (см. 1-ый семестр), она имеет предел, то есть ряд сходится.
возрастает и, по условию, ограничена. Следовательно, по теореме Вейерштрасса (см. 1-ый семестр), она имеет предел, то есть ряд сходится.
Простые следствия из этого критерия – очень полезные теоремы сравнения.
Теорема 1. Пусть для всех 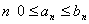 и пусть ряд
и пусть ряд  - сходится. Тогда сходится ряд
- сходится. Тогда сходится ряд  .
.
Доказательство. Очевидны неравенства  . По условию
. По условию  - сходится. Значит, по приведенному выше критерию,
- сходится. Значит, по приведенному выше критерию, 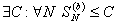 . Но тогда и
. Но тогда и  и, значит, ряд
и, значит, ряд  - сходится.
- сходится.
Примечание 1. Эта теорема может быть сформулирована и так: Пусть для всех 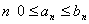 и ряд
и ряд  - расходится, тогда расходится и ряд
- расходится, тогда расходится и ряд  . Действительно, если бы этот ряд сходился, то первой теореме должен был бы сходиться и ряд
. Действительно, если бы этот ряд сходился, то первой теореме должен был бы сходиться и ряд  .
.
Примечание 2. Теорема 1 справедлива и в случае, когда неравенство 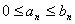 выполняется начиная с некоторого номера
выполняется начиная с некоторого номера 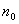 .
.
Теорема 2. Пусть 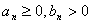 для всех
для всех 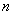 и
и 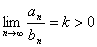 . Тогда либо оба ряда
. Тогда либо оба ряда  и
и  сходятся, либо они оба расходятся. (Т.е. не может быть так, что один из них сходится, а другой расходится).
сходятся, либо они оба расходятся. (Т.е. не может быть так, что один из них сходится, а другой расходится).
Доказательство. 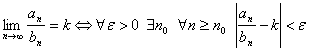 .Выберем
.Выберем 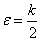 .Тогда
.Тогда 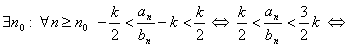 (т.к.
(т.к.  )
) 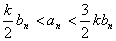 при
при 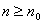 .
.
Если ряд  – сходится, то сходится и ряд
– сходится, то сходится и ряд 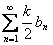 (по примечанию 2 к теореме 1). Тогда, взяв
(по примечанию 2 к теореме 1). Тогда, взяв 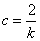 , получим, что и ряд
, получим, что и ряд  , т.е. ряд
, т.е. ряд  – сходится.
– сходится.
Если ряд  – сходится, то сходится и ряд
– сходится, то сходится и ряд 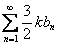 и, следовательно, сходится ряд
и, следовательно, сходится ряд  .
.
Теорема доказана.
Пример применения теоремы 2. Ряд 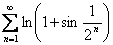 сходится, т.к.
сходится, т.к.  при
при 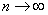 и ряд
и ряд 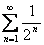 – сходится.
– сходится.
Сравнение рядов с положительными членами
Пусть имеем два положительных ряда с положительными членами:
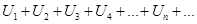 (1)
(1)
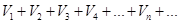 (2)
(2)
Для них справедливы следующие теоремы:
Теорема 1:
Если члены ряда (1) не больше соответствующих членов ряда (2), т.е.
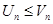

и ряд (2) сходится, то сходится и ряд (1).
Теорема 2:
Если члены ряда (1) не меньше соответствующих членов ряда (2), т.е.
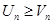

и ряд (2) расходится, то и ряд (1) расходится.
Важно!
Обе теоремы справедливы только для рядов с положительными членами или если некоторые члены ряда равны нулю.
|
из
5.00
|
Обсуждение в статье: Необходимое условие сходимости ряда. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

