 |
Главная |
Интегрирование выражений, содержащих тригонометрические функции
|
из
5.00
|
Рассмотрим основные случаи интегрирования выражений, содержащих тригонометрические функции.
При нахождении интегралов вида  ,
,
 ,
,  подынтегральные функции из произ-
подынтегральные функции из произ-
ведений преобразовываются в суммы с помощью формул:
 ,
,
 ,
,
 .
.
В результате полученные интегралы находятся с использованием методов интегрирования и таблицы интегралов. При этом можно использовать формулы  и
и  .
.
Интегралы вида 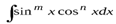 можно находить довольно просто в следующих случаях.
можно находить довольно просто в следующих случаях.
1.Если m – положительное нечётное число, то можно отделить первую степень синуса и применить подстановку  . Тогда
. Тогда  и подынтегральное выражение с помощью тригонометрических формул сведётся к степенным функциям.
и подынтегральное выражение с помощью тригонометрических формул сведётся к степенным функциям.
2.Если n - положительное нечётное число, то можно отделить первую степень косинуса и выполнить замену  . Тогда
. Тогда  и подынтегральное выражение с помощью тригонометрических функций тоже сведётся к степенным функциям.
и подынтегральное выражение с помощью тригонометрических функций тоже сведётся к степенным функциям.
3.Если m и n – неотрицательные чётные числа, то преобразование подынтегральных выражений можно выполнять с помощью формул понижения степени  и
и  .
.
4.Подынтегральная функция представляет собой дробь, в числителе которой находится степень синуса, а в знаменателе – степень косинуса, или наоборот. При этом показатели степени или оба чётные, или оба нечётные, т.е. одинаковой чётности.
В этом случае, если в числителе синус, то наиболее подходящей является подстановка  .Отсюда
.Отсюда  ,
,  ,
,  ,
,  .
.
Если же в числителе косинус, то удобно использовать подстановку  .Тогда
.Тогда  ,
,  ,
,  ,
,  .
.
5. Нахождение интегралов вида  сводится с помощью подстановки
сводится с помощью подстановки  к нахождению интегралов от рациональных функций. Подстановка
к нахождению интегралов от рациональных функций. Подстановка  называетсяуниверсальной тригонометрической подстановкой, которая всегда приводит к результату. В этом случае
называетсяуниверсальной тригонометрической подстановкой, которая всегда приводит к результату. В этом случае  ,
,  ,
,  ,
,  ,
,  .
.
Интегрирование иррациональных выражений. Интеграл от Дифференциального бинома.
а) Рассмотрим интегралы вида
 (2)
(2)
где R – рациональная функция от  переменных,
переменных,  - натуральные числа,
- натуральные числа, 
Пусть S – наименьший общий знаменатель дробей  Тогда с помощью замены
Тогда с помощью замены  интеграл (2) сводится к интегралу от рациональной функции переменного
интеграл (2) сводится к интегралу от рациональной функции переменного  .
.
Рассмотрим, например, интеграл
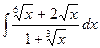 .
.
Выбирая наименьший общий знаменатель дробей  (то есть 6), сделаем замену
(то есть 6), сделаем замену  . Тогда
. Тогда  и
и

Остается вычислить последний интеграл, как это указано в интегрировании рациональных дробей.
б) При вычислении интегралов вида
1)  2)
2)  3)
3) 
где  - рациональная функция, удобно пользоваться следующими тригонометрическими подстановками соответственно:
- рациональная функция, удобно пользоваться следующими тригонометрическими подстановками соответственно:
 или
или  2)
2) 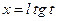 или
или  3)
3)  или
или 
В этом случае исходные интегралы сводятся к интегралам, описанным в универсальной триг подстановке и в интегрлах вида где
где и
и - целые числа.
- целые числа.
|
из
5.00
|
Обсуждение в статье: Интегрирование выражений, содержащих тригонометрические функции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

