 |
Главная |
Решение дифференциальных уравнений первого порядка с разделяющимися переменными
|
из
5.00
|
Введение
Учебно-методическое пособие написано для студентов заочной формы обучения в помощь в выполнении контрольных работ №1,2 дисциплины «Дополнительные главы математики».
Учебно-методическое пособие особенно полезно студентам, обучающимся по направлению подготовки 23.03.03 «Эксплуатация транспортно-технологических машин и комплексов», профиль «Автомобили и автомобильное хозяйство».
В пособии в краткой форме приводится теоретический материал, необходимый для выполнения контрольных работ, задачи с решениями. Так же в пособии представлены задания контрольных работ №1,2 и примеры их решения.
Обыкновенные дифференциальные уравнения и системы дифференциальных уравнений.
Основные определения и понятия
Дифференциальным уравнением (обыкновенным дифференциальным уравнением) называется соотношение  между независимой переменной х, функцией от неё у, и производными различного порядка от этой функции, записанное в форме равенства:
между независимой переменной х, функцией от неё у, и производными различного порядка от этой функции, записанное в форме равенства:

В частных случаях в указанное соотношение может не входить независимая переменная или функция от неё, или и то и другое, но обязательно должна входить производная (производные), иначе данное соотношение нельзя назвать дифференциальным уравнением.
Наибольший порядок производной, входящей в уравнение, определяет и порядок уравнения.
Решением дифференциального уравнения называется всякая функция у, которая при подстановке в уравнение обращает его в тождество.
Решение, полученное в виде:  , где
, где  – произвольные константы, число которых соответствует порядку уравнения, называется общим.
– произвольные константы, число которых соответствует порядку уравнения, называется общим.
Решение, полученное при наличии ряда условий, когда произвольные константы принимают вполне определенные значения, называется частным.
Решение уравнения, представленное в виде:  , называется общим интегралом; при конкретных значениях произвольных констант оно называется частным интегралом.
, называется общим интегралом; при конкретных значениях произвольных констант оно называется частным интегралом.
Решение, которое нельзя получить из общего ни при каких значениях произвольных постоянных, называется особым. Заметим, что в дальнейшем нахождение особых решений уравнений не рассматривается.
График функции, являющейся решением дифференциального уравнения, называется интегральной кривой.
Решение дифференциальных уравнений первого порядка с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение, которое можно представить в виде:
 (1)
(1)
или
 . (1¢)
. (1¢)
Рассмотрим примеры решения таких уравнений.
Пример 1. Найти общий интеграл уравнения
 .
.
Решение.
Представим уравнение в виде:  .
.
Чтобы разделить переменные, поделим обе части равенства на выражение  , получим: .
, получим: .
Интегрируем обе части данного уравнения:  .
.
Получим ответ:  .
.
Проверим найденное решение. Следует сказать, что проверка может оказаться сложнее, чем нахождение решения, особенно, если оно получено в неявной форме. Чтобы её выполнить, нужно иметь хорошие навыки дифференцирования. Достаточно легко проверка выполняется в линейных уравнениях, т.к. их решение получается в явном виде.
Для проверки выразим из общего интеграла 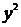 :
:


 .
.
Продифференцируем обе части последнего равенства по 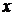 :
:
 .
.
Разделим обе части данного уравнения на 2 и умножим на  :
:
 , напомним, что
, напомним, что  .
.
Подставим полученное выражение в правую часть исходного уравнения, записанного в виде:  .
.
 .
.
Проверка выполнена, решение верное.
В дальнейшем проверка решений обычно не приводится, но предполагается, что она выполнена.
Пример 2. Найти частное решение уравнения 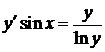 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  .
.
Решение.
Полагая  , перепишем данное уравнение в виде
, перепишем данное уравнение в виде  .
.
Разделяем переменные:  .
.
Интегрируем обе части уравнения:  , или
, или  , получим
, получим  – общий интеграл.
– общий интеграл.
Теперь найдем С. Положим 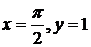 , тогда
, тогда  Þ
Þ  .
.
Подставляя значение  в выражение общего интеграла, найдем частный интеграл уравнения:
в выражение общего интеграла, найдем частный интеграл уравнения:  .
.
Во многих практических задачах решение нужно получить в явном виде и для его проверки и для анализа поведения той функции, для нахождения которой и было составлено дифференциальное уравнение. Покажем на примере данного уравнения, как это можно сделать.
Умножим обе части написанного равенства на 2, получим:  или
или  , тогда
, тогда  . Чтобы избавиться от логарифма, применим обратную функцию – показательную, такая операция называется потенцированием:
. Чтобы избавиться от логарифма, применим обратную функцию – показательную, такая операция называется потенцированием:
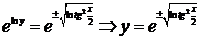
|
из
5.00
|
Обсуждение в статье: Решение дифференциальных уравнений первого порядка с разделяющимися переменными |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

