 |
Главная |
Нахождение приближённого решения дифференциальных уравне- ний
|
из
5.00
|
Обычный путь решения дифференциальных уравнений – это решение их в квадратурах, т.е. с помощью интегрирования. Термин «квадратура» происходит от геометрического смысла определённого интеграла  , который равен площади (квадратуре) криволинейной трапеции, фигуры, образованной линиями
, который равен площади (квадратуре) криволинейной трапеции, фигуры, образованной линиями  , при условии, что график последней расположен выше оси абсцисс.
, при условии, что график последней расположен выше оси абсцисс.
Однако существуют дифференциальные уравнения, к которым такой способ решения не применим. В этом случае можно найти их решение приближённо, например, в виде суммы степенных функций:
 (1)
(1)
В написанной формуле 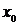 - это значение аргумента, при котором известно значение функции. Коэффициенты
- это значение аргумента, при котором известно значение функции. Коэффициенты  при степенных функциях можно найти различными способами, наверное, самый удобный – нахождение их таким же образом, как в формуле Тейлора:
при степенных функциях можно найти различными способами, наверное, самый удобный – нахождение их таким же образом, как в формуле Тейлора:
 , где
, где  - производная порядка
- производная порядка 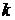 , вычисленная при
, вычисленная при  , при данном способе обозначения производная нулевого порядка – это сама функция.
, при данном способе обозначения производная нулевого порядка – это сама функция.
Тогда формула (1) примет вид:
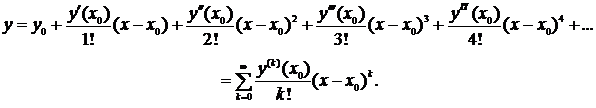
Как видим, для нахождения точного решения нужно найти бесконечное количество слагаемых. Поскольку это невозможно, ограничиваются несколькими слагаемыми, тогда решение будет найдено приближённо:
 .
.
Тригонометрические ряд. Ряд Фурье.
Функциональный ряд называется тригонометрическим, если членами ряда являются синусы и косинусы кратных значений аргумента x, то есть ряд вида
 (1)
(1)
1.Пусть функция  - периодическая с периодом
- периодическая с периодом 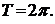 Рядом Фурье для функции
Рядом Фурье для функции 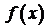 называется тригонометрический ряд (1), коэффициенты которого (коэффициенты Фурье) находятся по формулам:
называется тригонометрический ряд (1), коэффициенты которого (коэффициенты Фурье) находятся по формулам:
 Если разлагаемая в ряд Фурье функция
Если разлагаемая в ряд Фурье функция  - нечетная, то
- нечетная, то
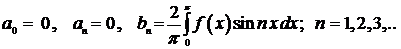
Если функция  - четная, то
- четная, то

Условия разложимости функции в ряд Фурье определяются следующей теоремой.
Теорема (Дирихле).
Если функция  - периодическая с периодом
- периодическая с периодом  на отрезке
на отрезке  непрерывна или имеет конечное число точек разрыва первого рода и если этот отрезок можно разбить на конечное число отрезков так, что внутри каждого из них функция
непрерывна или имеет конечное число точек разрыва первого рода и если этот отрезок можно разбить на конечное число отрезков так, что внутри каждого из них функция  монотонна, то ряд Фурье для этой функции сходится для всех значениях х и сумма полученного ряда равна значению функции
монотонна, то ряд Фурье для этой функции сходится для всех значениях х и сумма полученного ряда равна значению функции  в точках её непрерывности. В точках разрыва функции сумма ряда равно среднему арифметическому односторонних пределов в этих точках, т.е.
в точках её непрерывности. В точках разрыва функции сумма ряда равно среднему арифметическому односторонних пределов в этих точках, т.е.
 где
где 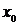 - точка разрыва.
- точка разрыва.
2. Если функция  - периодическая с периодом
- периодическая с периодом  , то коэффициенты ряда Фурье
, то коэффициенты ряда Фурье


вычисляются по формулам:
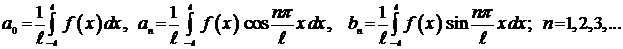
Если функция  - нечетная, то
- нечетная, то


Если функция  - четная, то
- четная, то

Пример. Разложить в ряд Фурье функцию  с периодом
с периодом  .
.
Решение. Данная Функция удовлетворяет условиям сходимости теоремы Дирихле. Следовательно, она допускает разложение в ряд Фурье
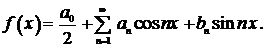
Функция  нечетная, поэтому
нечетная, поэтому 
Найдем коэффициент  :
: 



Таким образом,

|
из
5.00
|
Обсуждение в статье: Нахождение приближённого решения дифференциальных уравне- ний |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

