 |
Главная |
Задачи различного характера на составление дифференциаль ных уравнений
|
из
5.00
|
При решении таких задач для составления уравнения используют соотношение между малым изменением (дифференциалом) одной величины (функции) и соответствующим малым изменением (дифференциалом) другой величины, которая рассматривается как независимая переменная. В качестве такой независимой переменной часто выступает время. Отношение дифференциала функции к дифференциалу независимой переменной (производная) имеет смысл скорости изменения функции, это понятие также часто используется при составлении дифференциальных уравнений. Кроме того, решение задач из физики, химии, биологии и тому подобное, естественно требует некоторых знаний из соответствующих тем.
Пример 1. Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый данный момент времени его фактической стоимости. Начальная стоимость равна A0. а) Найти зависимость стоимости оборудования от времени; б) найти стоимость оборудования в момент времени 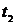
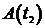 , если известна его стоимость в момент времени
, если известна его стоимость в момент времени 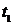
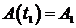 .
.
Решение.
а) Обозначим 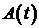 - стоимость оборудования в момент времени t. Пусть за промежуток времени dt стоимость уменьшилась на величину dA. Тогда скорость обесценивания равна
- стоимость оборудования в момент времени t. Пусть за промежуток времени dt стоимость уменьшилась на величину dA. Тогда скорость обесценивания равна 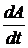 . Т.к. она пропорциональна фактической стоимости, то можно написать
. Т.к. она пропорциональна фактической стоимости, то можно написать 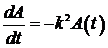 ;
; 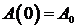 , где
, где 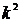 - коэффициент пропорциональности, знак минус отражает тот факт, что стоимость уменьшается.
- коэффициент пропорциональности, знак минус отражает тот факт, что стоимость уменьшается.
Решим составленное уравнение:
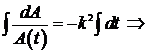
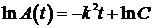 Þ
Þ 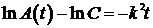
Þ 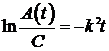 Þ
Þ 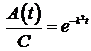 .
.
При 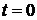
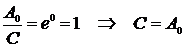 .
.
Тогда 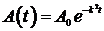 .
.
б) Используя условие 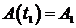 , найдем коэффициент пропорциональности.
, найдем коэффициент пропорциональности. 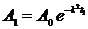 Þ
Þ 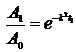 Þ
Þ 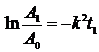 Þ
Þ 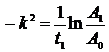 .
.
Тогда 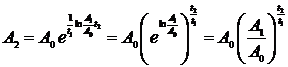 .
.
Пример 2. Некоторое вещество преобразуется в другое со скоростью, пропорциональной количеству не преобразованного вещества. По истечении времени t1первого вещества было m1, по истечение времени t2 – m2. Найти массу вещества в начале процесса; через какое время после начала реакции останется 1% исходного вещества?
Решение.
Пусть m0 - исходное количество вещества при t = 0,
m(t) - количество не преобразованного вещества в момент времени t.
Если за промежуток времени dt преобразуется dm первого вещества, то скорость преобразования 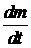 .
.
По условию задачи 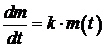 , где
, где 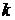 - коэффициент пропорциональности;
- коэффициент пропорциональности; 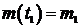 ;
; 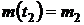 ,
,
Решаем уравнение: 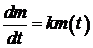 ; Þ
; Þ 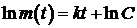 .
.
При t = 0 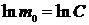 ,
, 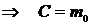 .
.
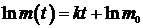 ;
; 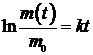 ,
, 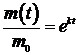 ;
; 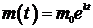 ;.
;.
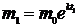 ,
, 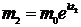 , разделим
, разделим 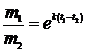 ;
;
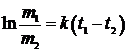 Þ
Þ  ;
;
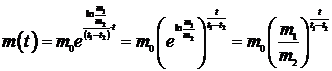 .
.
Для нахождения m0 возьмем t = t1.
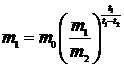 Þ
Þ 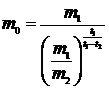 .
.
Для ответа на второй вопрос запишем:
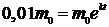 ;
; 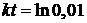 ;
; 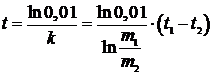 .
.
Пример 3. Задача истечения жидкости из сосуда через малое отверстие.
В общем виде задача формулируется следующим образом. Имеется сосуд, площадь поперечного сечения которого 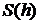 есть известная функция высоты уровня жидкости над отверстием, поперечное сечение – сечение, проведённое перпендикулярно оси симметрии сосуда. Сосуд (резервуар, бак) наполнен жидкостью до уровня
есть известная функция высоты уровня жидкости над отверстием, поперечное сечение – сечение, проведённое перпендикулярно оси симметрии сосуда. Сосуд (резервуар, бак) наполнен жидкостью до уровня 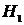 . В момент времени
. В момент времени 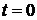 жидкость начинает вытекать из сосуда через малое отверстие площади
жидкость начинает вытекать из сосуда через малое отверстие площади 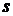 в самой нижней части сосуда. Определить время
в самой нижней части сосуда. Определить время 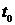 , за которое уровень жидкости понизится до значения
, за которое уровень жидкости понизится до значения 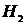 .
.
Решение.
Решение задачи основано на том, что изменение объема жидкости за небольшое время 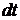 , связанное с понижением её уровня в сосуде, равно объёму жидкости, вытекающему за это время из отверстия. Изменение объёма, связанное с понижением уровня равно
, связанное с понижением её уровня в сосуде, равно объёму жидкости, вытекающему за это время из отверстия. Изменение объёма, связанное с понижением уровня равно 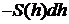 ,
, 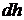 - изменение уровня за время
- изменение уровня за время 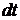 , знак минус отражает тот факт, что объём уменьшается. Количество жидкости, вытекающей из сосуда, равно
, знак минус отражает тот факт, что объём уменьшается. Количество жидкости, вытекающей из сосуда, равно 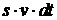 , где
, где 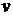 - скорость жидкости, вытекающей из сосуда. Согласно формуле Торричелли:
- скорость жидкости, вытекающей из сосуда. Согласно формуле Торричелли: 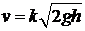 . В этой формуле
. В этой формуле 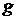 - ускорение свободного падения, приближённо равное 9,81
- ускорение свободного падения, приближённо равное 9,81 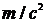 ,
, 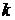 - коэффициент расхода, который определяется эмпирически, т.е. опытным путём, и зависит от жидкости. Для воды этот коэффициент примерно равен 0,62, для керосина – 0,6. Учитывая всё сказанное, получим уравнение:
- коэффициент расхода, который определяется эмпирически, т.е. опытным путём, и зависит от жидкости. Для воды этот коэффициент примерно равен 0,62, для керосина – 0,6. Учитывая всё сказанное, получим уравнение:
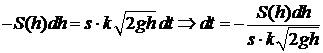 .
.
При изменении высоты уровня от 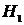 до
до 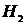 время изменится от 0 до
время изменится от 0 до 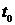 . Поэтому:
. Поэтому:
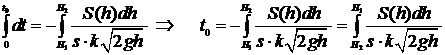 .
.
Вычисление интеграла в правой части зависит от формы сосуда, в котором находится жидкость, размеров и формы отверстия, через которое она вытекает. Для примера рассмотрим следующую задачу.
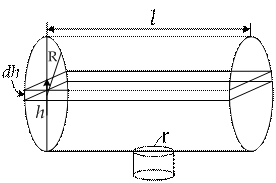 Цилиндрический резервуар длиной l и радиусом R расположен горизонтально. За какое время вода полностью вытечет из резервуара, если отверстие радиуса r находится на уровне самой нижней из образующих цилиндра.
Цилиндрический резервуар длиной l и радиусом R расположен горизонтально. За какое время вода полностью вытечет из резервуара, если отверстие радиуса r находится на уровне самой нижней из образующих цилиндра.
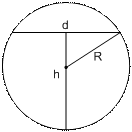 В данной задаче площадь поперечного сечения S(h) представляет собой прямоугольник, одна сторона которого фиксирована и равна l, другая зависит от h, назовем её d. Из рисунка видно, что
В данной задаче площадь поперечного сечения S(h) представляет собой прямоугольник, одна сторона которого фиксирована и равна l, другая зависит от h, назовем её d. Из рисунка видно, что
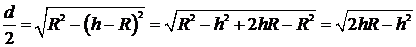 ;
;
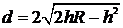 ,
,
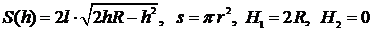 .
.
Тогда время истечения 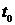 воды из резервуара равно:
воды из резервуара равно:
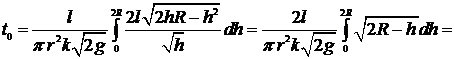
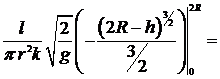
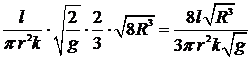 .
.
В частности, при 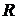 = 1 м,
= 1 м, 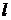 = 2 м,
= 2 м, 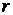 = 2,5 см, получим:
= 2,5 см, получим: 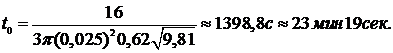
1.6. Дифференциальные уравнения вида 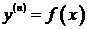
Общее решение получается путем n-кратного интегрирования. По определению, производная порядка п это производная от производной предыдущего порядка 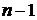 :
: 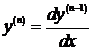 . Используя это определение, исходное уравнение можно записать в виде:
. Используя это определение, исходное уравнение можно записать в виде:
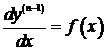 Þ
Þ 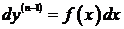 Þ
Þ 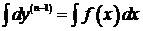 Þ
Þ 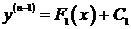 .
.
Используя 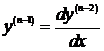 , получим
, получим 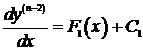 Þ
Þ 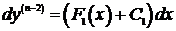 Þ
Þ 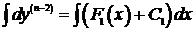 Þ
Þ 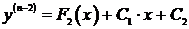 .
.
Понижение порядка уравнения продолжается до тех пор, пока не получим саму функцию y.
Пример 1. Найти общее решение уравнения 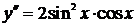 .
.
Решение.
Общее решение получается путем двукратного интегрирования данного уравнения.
1) 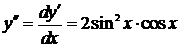 ,
, 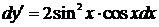 ,
,
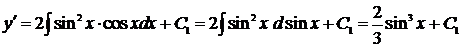 .
.
2) 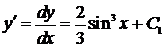 ,
, 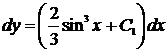 ,
, 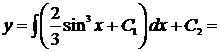
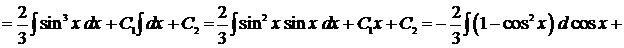
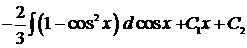
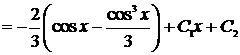 .
.
Пример 2. Найти частное решение уравнения 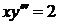 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 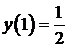 ;
; 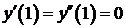 .
.
Решение.
Запишем уравнение в виде 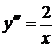 .
.
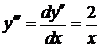 Þ
Þ 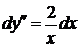 Þ
Þ 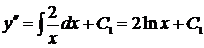 .
.
Найдем 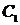 :
:  Þ
Þ 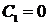 .
.
Следовательно: 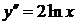 ,
, 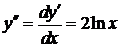 Þ
Þ 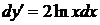 Þ
Þ
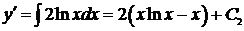 . (При нахождении
. (При нахождении 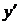 использован метод интегрирования по частям.) Найдем
использован метод интегрирования по частям.) Найдем 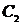 :
: 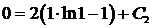 Þ
Þ 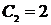 .
.
Следовательно: 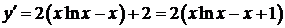 .
.
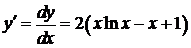 Þ
Þ 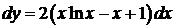 Þ
Þ
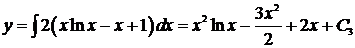 . (Снова использован метод интегрирования по частям.) Найдем
. (Снова использован метод интегрирования по частям.) Найдем 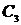 :
: 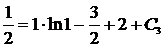 Þ
Þ 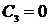 .
.
Ответ: 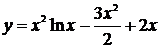 .
.
|
из
5.00
|
Обсуждение в статье: Задачи различного характера на составление дифференциаль ных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

