Задачи на составление дифференциальных уравнений

Как уже говорилось, к составлению дифференциальных уравнений приводят задачи, встречающиеся в различных областях науки: физики, биологии, математики и др. Вначале из этого широкого круга задач рассмотрим геометрические задачи, требующие для нахождения ответа составления и решения дифференциальных уравнений.

1.5.1. Задачи с геометрическим содержанием на составление диффе- ренциальных уравнений

В этих задачах необходимо найти (составить) уравнение линии по заданному свойству её касательной или нормали. Вместо слова линия часто используют слово кривая.

При рассмотрении примеров будут использованы следующие термины:

точка 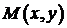- произвольная точка на искомой кривой; MT - касательная; MN - нормаль; TA - подкасательная; AN - поднормаль; a - угол, образованный касательной с положительным направлением Ох; tg a - угловой коэффициент касательной. Также используется геометрический смысл производной: значение производной в точке касания равно угловому коэффициенту касательной 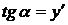. При составлении уравнений на данную тему полезно помнить уравнение касательной: 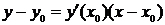и нормали (прямой, проходящей через точку касания перпендикулярно касательно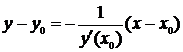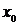й): , и 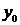- абсцисса и ордината точки касания.

Пример 1. Найти уравнение кривой, проходящей через точку P(1,2), для которой отрезок касательной между точкой касания и осью Ох делится пополам в точке пересечения с осью Оу.

Решение.

Пусть 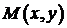- произвольная точка искомой кривой, MA - касательная к кривой, A - точка пересечения касательной с осью Ох, B - точка пересече ния с осью Оу, C - проекция точки M на ось Ох (см. рис.).

Обозначив через a угол, образованный касательной с положительным направлением оси Ох, будем иметь .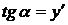

С другой стороны, из рисунка следует, что .

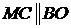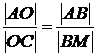Выразим это отношение через текущие координаты точки М. Так как , то , но 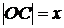, по условию 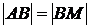, поэтому 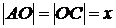и .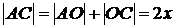

Кроме того, 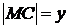. Таким образом, .

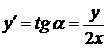Это дифференциальное уравнение первого порядка с разделяющимися переменными. Разделяем переменные и интегрируем: , ,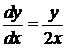

, , , , .

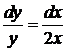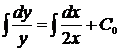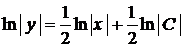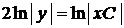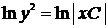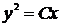Полученное общее решение определяет семейство парабол, проходящих через начало координат, с осью симметрии Ох.

Из полученного семейства интегральных кривых выделим теперь искомую кривую, удовлетворяющую начальному условию, т.е. проходящую через точку P(1,2).

Подставляя значения 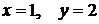в общее решение 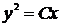, получим .

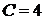Таким образом, уравнение искомой кривой имеет вид: .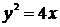

Ответ: .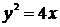

Пример 2. Найти уравнения кривых, для которых площадь треугольника, образованного осью Ох, касательной и радиус-вектором точки касания, постоянная величина, равная .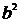

Решение.

Пусть 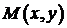- произвольная точка искомой кривой, MA - касательная к кривой, A - точка пересечения касательной с осью Ох, B - проекция точки M на ось Ох, OM - радиус-вектор точки M (см. рис.). Согласно условию задачи: (*)

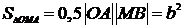Из рис. видно, что .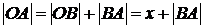

Из треугольника MBA найдем:

, , , .

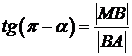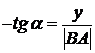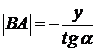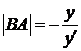Следовательно, .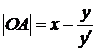

Подставляя в равенство (*) выражение для 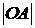и 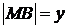и выполнив необходимые преобразования, получим дифференциальное уравнение первого порядка:

, , , .

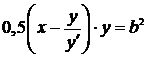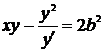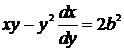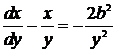Это линейное уравнение относительно функции 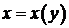. Интегрируем его с помощью замены :

; .

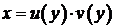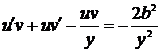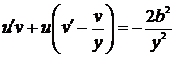Решаем систему: .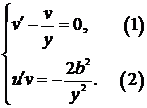

(1): , , , , .

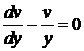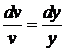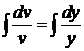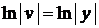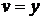Подставим 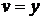во второе уравнение системы:

, , , .

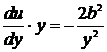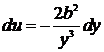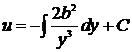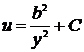Находим общее решение: 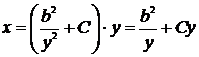, 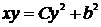. Оно определяет семейство кривых, удовлетворяющих условию задачи.

Ответ: .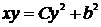

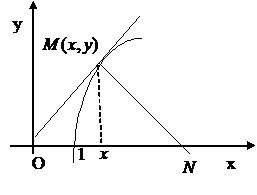Пример 3. Найти уравнение кривой, проходящей через точку (1; 0), если длина отрезка оси абсцисс, отсекаемого её нормалью, на 2 больше абсциссы точки касания.

Решение.

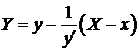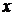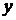Запишем уравнение нормали в виде: , где Х,Y – текущие координаты точек нормали, и - абсцисса и ордината точки касания.

Проведем нормаль MN в произвольной точке 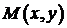к искомой кривой. Подставив координаты точки 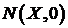в уравнение нормали, получим:

, , .

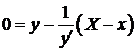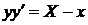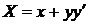Согласно условию 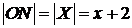. Следовательно, 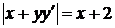. Раскрывая модуль, получим два уравнения:

1) , , , , , .

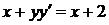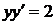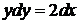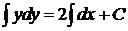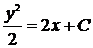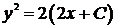Подставляя начальное условие 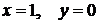в общее решение, получим .

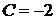Таким образом, уравнение искомой кривой имеет вид: .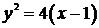

2) , , , ,

, , ,

.

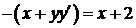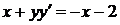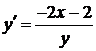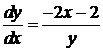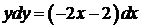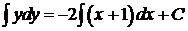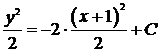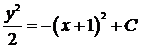Подставив начальное условие 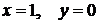в общее решение, получим 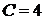. Следовательно, уравнение искомой прямой принимает вид

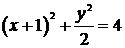или .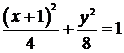

Пример 4. Найти уравнение кривой, у которой отрезок, отсекаемый касательной на оси ординат, равен поднормали.

Решение.

Пусть 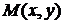- произвольная точка искомой линии, МТ - касательная, В – точка пересечения касательной с осью ОУ, А – проекция точки М на ось ОХ, МN – нормаль, АN – поднормаль. Обозначив через a угол, образованный касательной МТ с положительным направлением оси ОХ, получим .

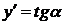В этой задаче берем уравнение касательной в виде уравнения прямой с угловым коэффициентом 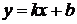, где , .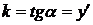

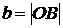По условию 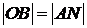. Найдем 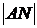из треугольника 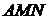(см. рис.):

.

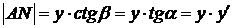Следовательно, уравнение касательной принимает вид .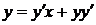

Преобразуя его, получим 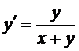, это однородное уравнение. Разделим числитель и знаменатель дроби на 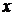, получим 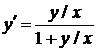. Сделаем замену 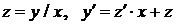, используя её, получим уравнение: 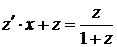. Выразим производную: 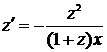. Представив 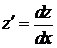и разделяя переменные, придём к равенству: 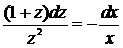. Интегрируя обе части этого равенства, придём к ответу.

.

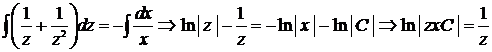Возвращаясь к исходным обозначениям, получим .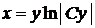

Полученное уравнение определяет совокупность линий, удовлетворяющих условию задачи.