Пример выполнения задания Д1

(Рассматривается выполнение только пункта 1 задания)

Рис. Д1

Груз М массой m = 20 кг начинает движение из точки D с начальной скоростью V₀ = 20 м/c. Его движение происходит по наклонной плоскости длины ℓ, составляющей угол α = 30^о с горизонтом, вдоль линии АВ наибольшего ската. Положение точки D задается величиной AD = S₀ = 10 м, вектор V₀ направлен параллельно прямой АВ к точке В. При движении по плоскости на груз действует постоянная сила Q = 100 Н, направление которой задается углом γ = 60^о, коэффициент трения скольжения между грузом и наклонной плоскостью равен f = 0,1. Через τ сек груз покидает плоскость или в точке А, или в точке В и, двигаясь далее в вертикальной плоскости под действием одной только силы тяжести через T секунд после отделения от плоскости попадает в точку С. Возможные варианты траекторий попадания груза в точку C показаны на рисунке.

Считая груз материальной точкой найти:

‒ точку (А или В) отрыва от плоскости,

‒ времяτ движения груза по наклонной плоскости,

‒ скорость груза в момент отрыва,

‒ координаты точки С приземления груза,

­‒ время T полета груза в воздухе,

‒ скорость груза в точке падения.

Решить задачу для двух значений начальной скорости:

V₀ = 25 м/c и V₀ = 20 м/c.

Решение 1

(дляначальной скоростиV₀ = 25 м/c)

 

1‒1. Изучение движения на участке АВ.

Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Для описания прямолинейного движения груза достаточно одной координатной оси х₁(рис. Д1‒1).

Рис. Д1‒1

Изобразим груз в произвольном положении и покажем действующие на него силы: силу тяжести груза G, нормальную реакцию N, заданную силу Q и силу трения скольжения F_тр (рис. Д1‒2).

Рис. Д1‒2

Составим дифференциальное уравнение движения груза вдоль оси 0х₁.

; (1.1)

Распишем входящие в уравнение силы: силу тяжести и силу трения скольжения, которая в общем случае вычисляется по формуле

F_тр = f∙N. (1.2)

Для определения нормальной реакции N проведем следующие рассуждения. Движение тела происходит вдоль оси 0х₁, а в направлении перпендикулярном этой оси никакого движения нет. Если на рисунке провести ось 0у₁,то дифференциальное уравнение движения груза вдоль этой оси имеет вид

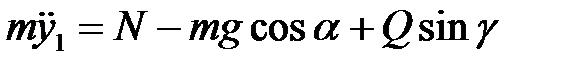. (1.3)

Величину нормальной реакции N найдем из уравнения (1.3), так как движения груза вдоль оси 0у₁ не происходит и, соответственно, =0,

. (1.4)

Таким образом, подставляя (1.2) и (1.4) в уравнение (1.1), получаем

. (1.5)

Подставляя численные значения, получим дифференциальное уравнение

. (1.6)

Полученное уравнение представляет собой дифференциальное уравнение второго порядка. Представив левую часть уравнения (1.6) в виде , получаем дифференциальное уравнение первого порядка

Для разделения переменных умножаем обе его части уравнения на dt

.

Вычисляем от обеих частей уравнения неопределенные интегралы

,

получаем первый интеграл от дифференциального уравнения движения тела или выражение скорости, в котором присутствует неизвестная величина С₁ (постоянная интегрирования).

. ( 1.7)

Для того чтобы проинтегрировать уравнений второй раз представим алгебраическое уравнение скорости в виде дифференциального уравнения первого порядка

.

Так же, как и ранее, умножаем обе его части уравнения на dt

и вычисляем от обеих частей уравнения неопределенные интегралы

,

в результате чего получаем второй интеграл от дифференциального уравнения движения тела или уравнение движения тела, в котором присутствуют две постоянных интегрирования С₁ и С₂.

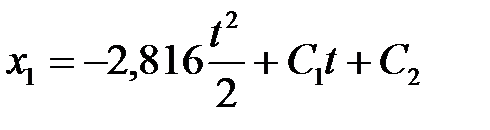. (1.8)

Найти постоянные интегрирования можно с помощью начальных условий, в качестве которых в механике используются значения координаты и скорости движущегося объекта в начальный момент времени. Для данной задачи начальные условия имеют вид

t = 0, x₁ = х₁₀ = 10 м, = V₀ = 25 м/с. (1.9)

Подставляя их сначала в первый

,

а затем во второй интегралы

10 ,

находим

С₁ = V₀ = 25, C₂ = х₁₀ = 10.

 

Подставляем найденные значения постоянных интегрирования в уравнения (1.7) и (1.8) получаем уравнение скорости и уравнение движения материальной точки в данной задаче

, (1.10)

. (1.11)

Для определения точки, в которой груз покидает плоскость, проведем следующие рассуждения. Предположим, что груз покидает плоскость в точке В. В момент достижения грузом этой точки время движения груза принимает значение, а координата х₁ становится равной ℓ = 100 м.

Подставляя эти значения в уравнение движения материальной точки (1.11), получаем

,

или

.

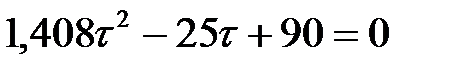Находим корни этого квадратного уравнения

.

Оба корня уравнения являются положительными и действительными

t₁= 5,018 с и τ₂ = 12,738 с.

Первое время t₁= 5,018 с соответствует достижению грузом точки В при движении по наклонной плоскости вверх (от А к В). Наличие второго времениτ₂ = 12,738 с объясняется следующим образом. Составленная математическая модель движения груза по наклонной плоскости в виде уравнения (1.11) не учитывает ограниченности длины этой плоскости (она предполагается бесконечной). Согласно этой модели груз движется вверх до его полной остановки, а затем под действием скатывающей силы начинает двигаться вниз, и, спустя τ₂ = 12,738 с после начала движения попадает в точку В двигаясь (по наклонной плоскости бесконечной длины) уже сверху вниз.

Для вычисления величины скорости V_В при отрыве груза от наклонной плоскости выбираем момент времени τ₁ = 5,018 с.

м/c.

1‒2. Изучение движения на участке ВС.

Перейдем к рассмотрению движения груза после отрыва от наклонной плоскости на участке ВС. Для описания криволинейного движения на этом участке необходимы две оси координат. Можно использовать приведенную на рисунке Д.1‒1 систему координат хАу, но лучше начало системы координат совместить с начальным (для этого участка движения) положением груза ‒ точкой В. Движение происходит под действием только силы тяжести G (рис. Д1‒3).

Рис. Д1‒3

Составим дифференциальные уравнения движения груза на этом участке:

.

Интегрируя дифференциальные уравнения дважды, получаем:

.

Запишем начальные условия движения груза в системе координат хВу, время будем отсчитывать от нуля:

. (1.12)

Используя начальные условия (1.12) найдем постоянные интегрирования:

;

.

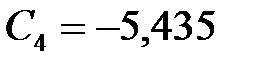Таким образом, постоянные интегрирования найдены, и, подставляя их значения в общее решение, получаем закон изменения проекций вектора скорости на оси координат и уравнения движения груза вдоль осей координат после отрыва:

(1.13)

(1.14)

; (1.15)

. (1.16)

Как видно из рисунка Д1‒3 существует три варианта полета груза и его соприкосновения с горизонтальной, вертикальной и наклонной плоскостями. Для того, чтобы выбрать один из этих вариантов, определим момент времени T_К, когда координатаx примет значение равное ширине рва d = 15м, т. е. . Подставляя данное условие в уравнение (1.14),

,

находим

T_K= 1,594 с.

Выяснить, по какой из трех траекторий происходит движение груза, можно путем вычисления для момента времени Т_К координаты у:

‒ если координата меньше у_К< 5 м, то груз пролетает выше точки К и падает на наклонную плоскость,

‒ если у_К = 5 м ‒ груз попадает точно в точку К,

‒ если у_К> 5 м, то груз находится ниже точкиК и возможно его попадание на вертикальную или горизонтальную поверхности рва (или в его угол):

‒ если 5 м <у_К< 70 м ‒ приземление на вертикальную поверхность рва и найденное время Т_К есть время полета груза,

‒ если у_К = 70 м ‒ приземление в углу рва, время Т_К также есть время полета груза,

‒ если у_К> 70 м ‒ приземление на горизонтальную поверхность рва, для нахождения времени полета груза Т следует решить уравнение (1.16) при y = h₂= 70 м).

Подставляя значение времени T_K= 1,594 с в уравнение (1.16), получаем

м.

Это означает, что груз пролетает над точкой К и приземляется на наклонную плоскость.

Найдем время Т прошедшее от момента отделения груза от наклонной плоскости АВ до момента его соприкосновения с наклонной поверхностью земли, а также координаты точки приземления x_C и y_C.

Анализ рисунка Д.1‒3 показывает, что в момент касания грузом наклонной плоскости в точке С, выполняется условие

;

при этом координаты точки К заданы по условию задания, а координаты точки С находятся путем подстановки времени Т в уравнения (1.14) и (1.16)

.

В результате, получаем квадратное уравнение

4,9T²‒ 14,847T + 10 = 0,

корни которого равны

T₁= 1,011 c, T₂= 2,019 c.

Первый корень T₁ = 1,011 c соответствует моменту времени, когда груз летит надо рвом и пересекает воображаемое продолжение наклонной плоскости. Второй кореньT₂= 2,019 c соответствует времени приземления на наклонную плоскость. Следовательно, в качестве искомого параметра ‒ время полета груза ‒ принимаем T = 2,019 c.

Координаты точки приземления С можно вычислить, подставляя время T = 2,019 c в уравнения (1.14) и (1.16):

x_C = 9,412T = 19,003 м;

y_C = 4,9T² ‒ 5,435T = 9,000 м.

Найдем скорость груза в момент приземления V_С через проекции на оси координат (1.13) и (1.15):

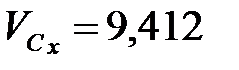м/с, м/с.

Тогда модуль скорости определится выражением

м/с.

 

Ответ: при начальной скорости груза V₀= 25 м/c получены следующие результаты:

‒ время движения по наклонной плоскости АВ τ = 5,018 с;

‒ точка отрыва от наклонной плоскости АВ ‒ точка В;

‒ скорость в момент отрыва в точке ВV_B = 10,869 м/c;

‒ время полета Т = 2,019 с;

‒ координаты точки приземления x_C = 19,006 м; y_C = 9,000 м;

‒ скорость касания с поверхностью земли V_C = 17,162 м/с.

 

Решение 2

(дляначальной скоростиV₀ = 20 м/c)

Рассмотрение движения груза на участке АВ полностью повторяет рассмотренный выше случай решения задания для начальной скорости V₀ = 25 м/с (до записи начальных условий в формуле 1.9) для определения постоянных интегрирования при решении дифференциального уравнения движения груза.

Ниже эта часть решения полностью повторяется(выделено шрифтом серого цвета), она воспроизводится с целью создания целостной картины порядка выполняемых действий по решению отдельной самостоятельной задачи.

2‒1. Изучение движения на участке АВ.

Рассмотрим движение груза на участке АВ, считая, считая груз материальной точкой. Для описания прямолинейного движения груза достаточно одной координатной осих₁ (Рис. Д1‒4).

Рис. Д1‒4

Изображаем груз в произвольном положении и показываем действующие на него силы: силу тяжести груза G, нормальную реакцию N, заданную силу Q и силу трения скольжения F_тр (Рис. Д1‒5).

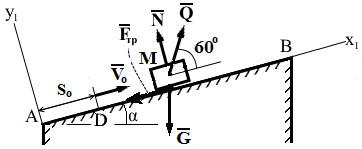
Рис. Д1‒5

Составим дифференциальное уравнение движения груза вдоль оси 0х₁.

;(1.1)

Распишем входящие в уравнение силы: силу тяжести и силу трения, которая в общем случае вычисляется по формуле

F_тр = f∙N. (1.2)

Для определения нормальной реакции N проведем следующие рассуждения. Движение тела происходит вдоль оси 0х₁, а в направлении перпендикулярном этой оси никакого движения нет. Если на рисунке провести ось 0у₁,то дифференциальное уравнение движения груза вдоль этой оси имеет вид

. (1.3)

Величину нормальной реакции N найдем из уравнения (2), так как =0,

. (1.4)

Таким образом,

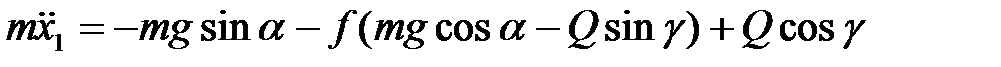. (1.5)

Подставляя численные значения, получим дифференциальное уравнение

. (1.6)

Полученное уравнение представляет собой дифференциальное уравнение второго порядка. Представив левую часть уравнения в виде , получаем дифференциальное уравнение первого порядка

Для разделения переменных умножаем обе его части уравнения на dt

.

Вычисляем от обеих частей уравнения неопределенные интегралы

,

получаем первый интеграл от дифференциального уравнения движения тела или выражение скорости, в котором присутствует неизвестная величина С₁ (постоянная интегрирования).

. (1.7)

Для того чтобы проинтегрировать уравнений второй раз представим алгебраическое уравнение скорости в виде дифференциального уравнения первого порядка

.

Так же, как и ранее, умножаем обе его части уравнения на dt

и вычисляем от обеих частей уравнения неопределенные интегралы

,

в результате чего получаем второй интеграл от дифференциального уравнения движения тела или уравнение движения тела, в котором присутствуют две постоянных интегрирования С₁ и С₂.

. (1.8)

Найти постоянные интегрирования можно с помощью начальных условий, в качестве которых в механике используются значения координаты и скорости движущегося объекта в начальный момент времени.

 

Для данной задачи начальные условия имеют вид

t = 0, x₁ = х₁₀ = 10 м, 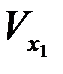= V₀= 20 м/с.

Подставляя их сначала в первый

,

а затем во второй интегралы

10 ,

находим

С₁ = V₀ = 20, C₂ = х₁₀ = 10.

Подставляем найденные значения постоянных интегрирования в уравнения (1.7) и (1.8) получаем уравнение скорости и уравнение движения материальной точки в данной задаче

, (1.17)

. (1.18)

 

Для определения точки, в которой груз покидает плоскость, проведем следующие рассуждения. Предположим, что груз покидает плоскость в точке В. В момент достижения грузом этой точки время движения груза равно τ, а координата х₁ равна ℓ = 100 м.

Подставляя эти значения в уравнение движения материальной точки (1.18), получаем

,

или

.

Находим корни этого квадратного уравнения

Так как дискриминант является отрицательным, то квадратное уравнение не имеет действительных корней. Это означает, что груз не достигает точки В, а двигаясь из точки D по наклонной плоскости вверх, в некоторый момент времени останавливается (точку остановки обозначим Е), а затем скользит вниз и покидает наклонную плоскость к точке А.

Определим момент времениτ₁, в который происходит остановка груза, для чего используем условие равенства нулю скорости груза в момент его остановки

,

откуда находим

τ₁ = 7,102 с.

Вычислим координату точки остановки Е

.

Таким образом, в момент остановки при t = τ₁ = 7,102 с координата и скорость груза равны

,

Эти условия являются начальными для движения груза по наклонной плоскости вниз.

В подтверждение того, что в момент времени τ₁начинается движение вниз, приведем следующие соображения. Хотя скорость груза в этот момент времени равна нулю, это вовсе не означает, что и ускорение равно нулю, ведь для того, чтобы в следующий момент времени появилась скорость, в данный момент должно быть направленное вниз ускорение. А наличие такого ускорения обуславливается действием направленной вниз вдоль наклонной плоскости результирующей силы, что подтверждается следующими расчетами.

Величина нормальной реакции

.

Максимальное значение силы трения

.

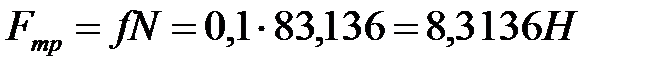Скатывающая сила

.

Сравнение величин скатывающей силы и препятствующей движению вниз силы трения скольжения, показывает, что результирующая сила действительно направлена вниз.

Для изучения движения груза от точки Е до точки А покажем действующие на этом участке силы (Рис. Д1‒6).

Рис. Д1‒6

Дифференциальное уравнение груза на участке ЕА имеет вид:

,

или

(1.19)

Здесь учтено, что поскольку груз движется вниз, то сила трения скольжения направлена вдоль наклонной плоскости вверх. Данное уравнение отличается от уравнения (1.1) знаком проекции силы трения скольжения . Подставляя значения заданных по условию задачи величин, получаем

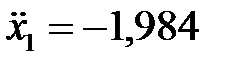
Интегрируя дважды, получаем

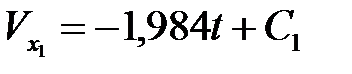; (1.20)

. (1.21)

Для определения постоянных интегрирования воспользуемся начальными условиями, т. е. значениями кинематических характеристик, при которых груз начал свое движение из точки Е вниз (отсчет времени начинаем заново).

t= 0 ,

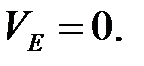
Подставляя начальные условия в уравнения (1.19) и (1.20), находим:

, .

Уравнение скорости и закон движения груза на участке ЕА с учетом найденных значений С₁ и С₂ принимают вид

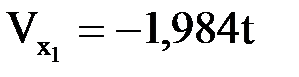, (1.22)

. (1.23)

Найдем время движения груза τ₂по наклонной плоскости вниз. Когда груз достигает точки A, то

.

Получаем уравнение

,

откуда

τ₂= 9,038с.

Из уравнения (1.23) найдем величину скорости груза в точке А при его отрыве от наклонной плоскости

м/c.

Направление вектора скорости V_A показано на рисунке Д1‒7.

Рис. Д1‒7

Время движения груза по наклонной плоскости найдем как сумму времени τ₁ движения от точки D до точки остановки Е и времени τ₂ движения груза после остановки от точки Е вниз до отрыва в точке А

t = τ₁ + τ₂ = 7,102 + 9,038 = 16,140 с.

2‒1. Изучение движения на участке АС.

Рассмотрим движение груза после отрыва его от наклонной плоскости (участок АС). Движение происходит под действием только силы тяжести G, используем систему координат хАу (рис Д1‒8).

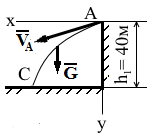
Рис. Д1‒8

Составим дифференциальные уравнения движения груза на этом участке:

.

Интегрируядифференциальные уравнения дважды, получаем:

Запишем начальные условия движения груза в системе координат хАу, время будем опять отсчитывать от нуля:

.

Используя начальные условия найдем постоянные интегрирования:

;

.

Таким образом, постоянные интегрирования найдены, и подставляя их значения в общее решение, получаем закон изменения проекций вектора скорости на оси координат и уравнения движения груза вдоль осей координат после отрыва:

(1.24)

(1.25)

; (1.26)

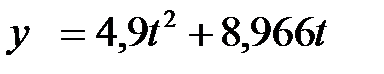. (1.27)

Найдем время Т, спустя которое после отделения от наклонной плоскости груз упадет на горизонтальную плоскость, и координаты точки падения x_C и y_C.

В момент приземления груза в точку С на наклонной плоскости координата у = у_С = h₁. Подставляя это значение в уравнение (1.27), получим квадратное относительно Т уравнение

4,9T² + 8,966T – 40 = 0.

Корни этого квадратного уравнения имеют значения

T₁ = 2,085 c, T₂ = ‒ 3,915 c.

Время не может быть отрицательным, следовательно

T = 2,085 c.

Координаты точки приземления С могут быть вычислены подстановкой в уравнения (1.25) и (1.27) найденного времени Т:

x_C = 15,528∙2,085 = 32,376 м;

y_C= 4,9∙(2,085)² + 8,966∙2,085 = 40м.

Подстановкой в уравнения (1.24) и (1.26) времени Т определим проекции скорости груза в момент в момент его падения на горизонтальную поверхность:

м/с;

= 29,400 м/с,

что позволяет вычислить модуль скорости груза в точке С

м/с.

Ответ:

‒ точкой отрыва груза от плоскости является точкаА,

‒ времяτ движения груза по наклонной плоскости до точки отрыва

τ= 16,140с,

‒ величина скорости груза в момент отрыва ,

‒ координаты точки С приземления груза x_C = 32,376 м;y_C= 40 м,

­‒ время полета груза в воздухе T = 2,085 c,

‒ скорость груза в точке падения м/с.

 

 

Литература

1. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Т.I и II. − М. : Наука, 1984.

2. Королёв Ю.В. Теоретическая механика. Курс лекций. − Иркутск : Изд-во ИрГТУ, 2006.

3. Королев Ю.В. Теоретическая механика. Учимся решать задачи : учебное пособие для самостоятельной работы. Ч. 1 : Статика, 2015. - 108 с.

4. Королев Ю.В. Теоретическая механика. Учимся решать задачи : учебное пособие для самостоятельной работы. Ч. 2 : Кинематика, 2015. - 107 с.

5. Королев Ю.В. Теоретическая механика. Учимся решать задачи : учебное пособие для самостоятельной работы. Ч. 3 : Динамика материальной точки, 2016. - 134 с.

6. Сборник заданий для курсовых работ по теоретической механике : учебное пособие для втузов / А. А. Яблонский [и др.]; под общ. ред. А. А. Яблонского, 2010. - 385 с.

7. Тарг С. М. Краткий курс теоретический механики. – М. : Высшая школа, 2009.

 

Приложение А

Форма задания на курсовую работу

 

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования