Парная регрессия и корреляция

Краткая теория

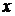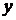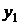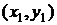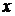Пусть для некоторой пары признаков и в результате проведения наблюдений получены следующие значения: , ,… ; , ,…, . Нанесем на декартову прямоугольную систему координат точки с координатами , ,…, . Полученная точечная диаграмма носит название поле корреляции. Анализ поля корреляции позволяет выдвинуть гипотезу о наличии связи между исследуемыми признаками и .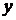

Парная регрессия – уравнение связи двух переменных:

,

где 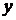– зависимая переменная (результативный признак);

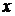– независимая, объясняющая переменная (фактор-признак).

Различают линейные и нелинейные регрессии.

Линейная регрессия: .

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, и регрессии, нелинейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

– полиномы разных степеней ;

– равносторонняя гипербола .

Регрессии, нелинейные по оцениваемым параметрам:

– степенная ;

– показательная ;

– экспоненциальная .

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 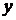от теоретических 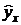минимальна, т.е.:

.

Для оценки параметров линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно и .

Решить данную систему линейных алгебраических уравнений можно любым известным способом или воспользоваться готовыми формулами:

,

.

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции для линейной регрессии:

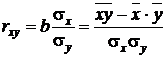
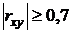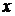Величина коэффициента находится в интервале . При этом чем ближе по абсолютной величине к 1, тем связь сильнее, чем ближе по абсолютной величине к 0, тем связь слабее. В частности, если , то связь отсутствует, значение означает наличие сильной связи, а при говорят о существовании точной функциональной связи между исследуемыми признаками и 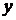. Знак коэффициента показывает направление связи: если , то связь прямая, то есть с увеличением признака 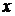признак 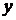увеличивается; если , то связь обратная, то есть с увеличением признака 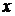признак 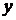уменьшается.

Тесноту связи изучаемых явлений для нелинейной регрессии оценивает индекс корреляции :

.

Величина коэффициента находится в интервале . Оценка тесноты связи с помощью проводится аналогично оценке тесноты связи с помощью с той лишь разницей, что по индексу нельзя делать выводы о направлении связи.

Оценку качества построенной модели дают коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Коэффициент (индекс) детерминации есть квадрат показателя корреляции, то есть для линейной регрессии и 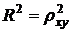для нелинейной. Величина показывает на сколько процентов вариация результативного признака 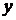объясняется вариацией учтенного в модели объясняющего фактора .

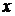Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:

,

где 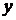-фактические значения,

а 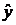-теоретические (расчетные) значения, получаемые путем подстановки фактических значений 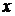в полученное уравнение регрессии

Допустимый предел значений – не более 8–10 %. Если > 10 %, то качество построенной модели признается неудовлетворительным, такую модель нельзя использовать при анализе и прогнозе.

Средний коэффициент эластичности оценивает силу влияния фактора на результат и показывает, на сколько процентов в среднем по совокупности изменится результат 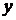от своей средней величины при изменении фактора 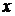на 1 % от своего среднего значения:

.

Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

,

где – общая сумма квадратов отклонений;

– сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);

– остаточная сумма квадратов отклонений.

F-тест – оценивание качества уравнения регрессии состоит в проверке гипотезы о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического и критического (табличного) значений F-критерия Фишера. определяется по формуле:

,

где – число единиц совокупности (наблюдений).

– это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости – вероятности отвергнуть нулевую гипотезу при условии, что она верна. обычно принимается равным 0,05 или 0,01. 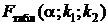для парной регрессии определяется по таблице и зависит от уровня значимости, числа степеней свободы и числа степеней свободы . Таблицу для определения , а также таблицы других используемых при решении задач статистик можно найти в приложениях.

Если , то гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. В противном случае гипотеза не отклоняется и признается статистическая незначимость, ненадёжность уравнения регрессии и показателя тесноты связи.

Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза о случайной природе показателей, т.е. незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия проводится путем сопоставления их значений с величиной случайной ошибки.

Случайные ошибки показателей и 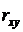определяются по формулам:

,

,

.

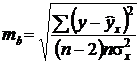Фактическиезначения t-критерия вычисляются следующим образом:

,

,

.

Критическое значение t-критерия определяется по таблице и зависит от уровня значимости и числа степеней свободы , где – число единиц совокупности (наблюдений).

Если , то гипотеза о случайной природе показателей отклоняется, т.е. , и не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора 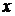. В противном случае гипотеза принимается и признается случайная природа формирования показателей , и .

Для расчета доверительных интервалов определяем предельную ошибку для каждого из показателей:

,

.

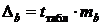Доверительные интервалы рассчитываются по формулам:

,

,

;

,

,

.

Если в границы доверительного интервала попадает нуль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр признается нулевым, статистически ненадежным, так как он не может одновременно принимать и положительные, и отрицательные значения.

Прогнозное значение определяется путем подстановки в уравнение регрессии 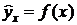соответствующего (прогнозного) значения . Вычисляется средняя стандартная ошибка прогноза :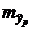

,

где ,

и строится доверительный интервал прогноза:

,

,

,

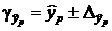где .

Прогноз признается надежным, если в границы его доверительного интервала не попал нуль.

Для оценки точности полученного прогноза вычисляется величина:

.

Чем ближе полученная величина к 1, тем прогноз точнее.