Множественная регрессия и корреляция

Краткая теория

Множественная регрессия – уравнение связи с несколькими независимыми переменными:

,

где 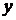– зависимая переменная (результативный признак),

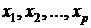–независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

– линейная: ;

– степенная: ;

– экспонента: ;

– гипербола: .

Можно использовать и другие функции, приводимые к линейному виду.

Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:

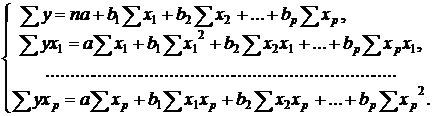
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе:

,

где , – стандартизованные переменные;

– стандартизованные коэффициенты регрессии.

Стандартизованные коэффициенты регрессии ( – коэффициенты) позволяют ранжировать факторы по силе влияния на результат: чем больше по абсолютной величине , тем сильнее фактор влияет на .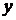

К уравнению множественной регрессии в стандартизованном масштабе применим МНК. – коэффициенты определяются из следующей системы уравнений:

Здесь , -линейные коэффициенты парной корреляции между соответствующими признаками.

Связь коэффициентов множественной регрессии 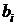со стандарти-зованными коэффициентам описывается соотношением:

.

Параметр определяется так: .

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле:

.

Для расчета частных коэффициентов эластичности применяется формула:

.

Коэффициенты эластичности могут быть использованы для ранжирования факторов по силе влияния на результативный признак.

Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

.

Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

.

Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде:

.

Частные коэффициенты корреляции, измеряющие влияние на 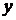фактора при неизменном уровне других факторов можно определить по рекуррентной формуле:

.

Частные коэффициенты корреляцииизменяются в пределах от -1 до 1. Они очищают парную зависимость данной пары признаков от влияния других факторов и дают более точную характеристику связи двух переменных. Частные и парные коэффициенты корреляции могут значительно отличаться друг от друга при наличии сильной межфакторной связи.

Качество построенной модели в целом оценивает коэффициент (индекс) множественной детерминации 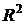, который рассчитывается как квадрат индекса множественной корреляции.

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается следующим образом:

,

где – число наблюдений;

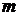– число факторов.

Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера. Фактическое значение критерия определяется по формуле:

.

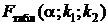определяется по уровню значимости (который обычно принимается равным 0,05 или 0,01), числу степеней свободы и числу степеней свободы .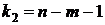

Если , то вероятностью делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи.

Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. Фактическое значение для него определяется по формуле:

.

А табличное значение 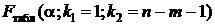зависит от уровня значимости , числа степеней свободы и числа степеней свободы .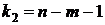

Оценку значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значения:

,

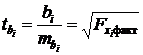где – средняя квадратическая ошибка коэффициента регрессии 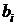, она может быть определена по следующей формуле:

.

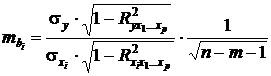При оценке значимости коэффициентов линейной регрессии с помощью t-статистики можно пользоваться следующим «грубым» правилом:

1) – практически стопроцентное свидетельство наличия связи;

2) 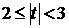говорит о весьма значимой связи (доверительная вероятность от 0,95 до 0,99);

3) если 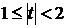, то сделанная оценка может рассматриваться как более или менее значимая (доверительная вероятность от 0,7 до 0,95 – уточняется по таблицам);

4) если 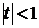, то коэффициент не может быть признан «хорошим» (значимым), поскольку доверительная вероятность здесь составит менее 0,7.

Конечно, при оценке надежности всегда играет роль число элементов совокупности, однако, при сформулированные правила практически всегда верны.

При построении уравнения множественной регрессии может возникнуть проблема мультиколлинеарности факторов, их тесной линейной связанности. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если . По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции . Чем ближе к 0 значение , тем сильнее мультиколлинеарность факторов и ненадежнее результаты регрессии. И наоборот, чем ближе к 1 значение , тем меньше мультиколлинеарность факторов. Коллинеарные факторы не следуют включать в модель одновременно.