 |
Главная |
АДДИТИВНАЯ И МУЛЬТИПЛИКАТИВНАЯ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ
|
из
5.00
|
Краткая теория
Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.
Временной ряд – это совокупность значения какого-либо показателя за несколько последовательных моментов или периодов.
Каждый уровень временного ряда ( 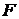 ) формируется из трендовой (
) формируется из трендовой ( 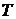 ), циклической (
), циклической ( 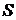 ) и случайной (
) и случайной ( 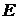 ) компонент.
) компонент.
Модели, в которых временной ряд представлен как сумма перечисленных компонент, – аддитивные модели, как произведение – мультипликативные модели временного ряда.
Аддитивная модель имеет вид: 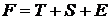 ; мультипликативная модель:
; мультипликативная модель: 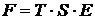 .
.
Построение аддитивной и мультипликативной моделей сводится к расчету значений Т, 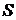 и
и 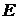 для каждого уровня ряда.
для каждого уровня ряда.
Построение модели включает следующие шаги:
1) выравнивание исходного ряда методом скользящей средней;
2) расчет значений сезонной компоненты 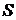 ;
;
3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной 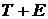 или в мультипликативной
или в мультипликативной 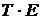 модели;
модели;
4) аналитическое выравнивание уровней 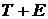 или
или 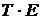 и расчет значений
и расчет значений 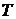 с использованием полученного уравнение тренда;
с использованием полученного уравнение тренда;
5) расчет полученных по модели значений 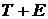 или
или 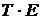 ;
;
6) расчет абсолютных и(или) относительных ошибок.
Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:
– линейная 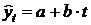 ;
;
– гипербола 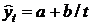 ;
;
– экспонента 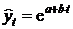 ;
;
– степенная функция 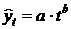 ;
;
– парабола второго и более высоких порядков 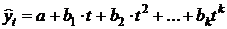 .
.
Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время 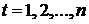 , а в качестве зависимой переменной – фактические уровни временного ряда
, а в качестве зависимой переменной – фактические уровни временного ряда 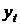 . Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации
. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации 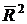 .
.
Десезонализация данных – это устранения влияния сезонной компоненты на уровни временного ряда.
Пример выполненной лабораторной работы № 4
Тема
Задание. Имеются поквартальные данные об объемах потребления электроэнергии жителям региона за 4 года (Таблица 5.2.1).
Таблица 5.2.1
| год | Квартал 1 | Квартал 2 | Квартал 3 | Квартал 4 |
Требуется:
1) Построить аддитивную модель;
2)Постоить мультипликативную модель;
3) Выполнить прогноз потребления электроэнергии на первый квартал 2014 года.
Решение.
1) Аддитивная модель
Шаг 1.Проведем выравнивание исходных уровней ряда методом скользящей средней, для этого:
1. Просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени.
2.Разделив полученные суммы на четыре, найдем скользящую среднюю. Полученные таким образом значения не содержат сезонной компоненты.
3.Приведем эти значения в соответствии с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних – центрированные скользящие средние.
Шаг 2.Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними. Результат занесем в таблицу (Таблица 5.2.2).
Таблица 5.2.2
| Квартал,t | уt | итого за 4к | скол.среднее | центриров. Ск.ср. | оценка сезон.комп. |
| 36,75 | |||||
| 39,375 | 9,625 | ||||
| 47,25 | 44,625 | 17,375 | |||
| 49,625 | -6,625 | ||||
| 56,25 | 54,125 | -19,125 | |||
| 60,5 | 58,375 | 9,625 | |||
| 65,25 | 62,875 | 16,125 | |||
| 70,5 | 67,875 | -7,875 | |||
| 76,75 | 73,625 | -19,625 | |||
| 81,75 | 79,25 | 9,75 | |||
| 84,375 | 19,625 | ||||
| 91,25 | 89,125 | -9,125 | |||
| 97,25 | 94,25 | -19,25 | |||
| 77,25 | |||||
Используем полученные оценки для расчета значений сезонной компоненты 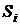 . Для этого найдем средние значения за каждый квартал по всем годам.
. Для этого найдем средние значения за каждый квартал по всем годам.
В моделях с сезонной компонентой обычно предполагается, что сезонные взаимодействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. Этот факт мы будем использовать для корректировки сезонной компоненты (Таблица 5.2.3).
Таблица 5.2.3
| Показатель | год | квартал1 | квартал2 | квартал3 | квартал4 |
| 9,625 | 17,375 | ||||
| -6,625 | -19,125 | 9,625 | 16,125 | ||
| -7,875 | -19,625 | 9,75 | 19,625 | ||
| -9,125 | -19,25 | - | - | ||
| итого за iкв | -23,625 | -58 | 53,125 | ||
| ср.оценка сез.комп. | -7,875 | -19,3333 | 9,666667 | 17,70833 | |
| скорректир.сез комп. | -7,91667 | -19,375 | 9,625 | 17,66667 |
Сумма значенийсезонной компоненты по всем кварталам составит:
-7,875-19,3333+9,666667+17,70833 =0,166667;
Определим корректирующий коэффициент:
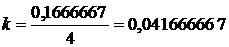 .
.
Рассчитаем скорректированные значениясезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом:
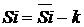 ,
,
где i=1,2,3,4. Проверим условие равенства нулевой суммой значений сезонной компоненты: -7,91667-19,375+9,625+17,66667=0;
Шаг 3.Устраним сезонную компоненту, вычитая ее значение из каждого уровня исходного временного ряда. Эти значения рассчитываются для каждого момента времени и содержат только тенденцию и случайную компоненту (Таблица 5.2.4).
Таблица 5.2.4
| t | yt | Si | yt-Si | T |
| -7,875 | 29,875 | 28,6901 | ||
| -19,3333 | 33,3333 | 33,7592 | ||
| 9,666667 | 39,33333 | 38,8283 | ||
| 17,70833 | 44,29167 | 43,8974 | ||
| -7,875 | 50,875 | 48,9665 | ||
| -19,3333 | 54,3333 | 54,0356 | ||
| 9,666667 | 58,33333 | 59,1047 | ||
| 17,70833 | 61,29167 | 64,1738 | ||
| -7,875 | 67,875 | 69,2429 | ||
| -19,3333 | 73,3333 | 74,312 | ||
| 9,666667 | 79,33333 | 79,3811 | ||
| 17,70833 | 86,29167 | 84,4502 | ||
| -7,875 | 87,875 | 89,5193 | ||
| -19,3333 | 94,3333 | 94,5884 | ||
| 9,666667 | 96,33333 | 99,6575 | ||
| 17,70833 | 110,2917 | 104,7266 |
Шаг 4. Определим компоненту Т для данной модели путем построения линейного тренда по данным, находящимся в столбце 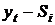 .
.
Получим тренд (Рисунок 5.2.1.):
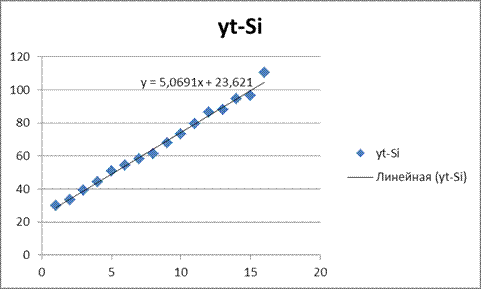
Рисунок 5.2.1
2) Мультипликативная модель.
Шаг 1.Выравнивание исходных уровней ряда методом скользящей средней были выполнены при построении аддитивной модели.
Шаг 2.Найдем оценки сезонной компоненты как отношение фактических уровней ряда к центрированным скользящим средним. Результат занесем в таблицу (Таблица 5.2.5).
Таблица 5.2.5
| Квартал,t | уt | итого за 4к | скол.среднее | центриров. Ск.ср. | оценка сезон.комп. |
| - | |||||
| 36,75 | - | ||||
| 39,375 | 1,244444444 | ||||
| 47,25 | 44,625 | 1,389355742 | |||
| 49,625 | 0,866498741 | ||||
| 56,25 | 54,125 | 0,64665127 | |||
| 60,5 | 58,375 | 1,164882227 | |||
| 65,25 | 62,875 | 1,256461233 | |||
| 70,5 | 67,875 | 0,883977901 | |||
| 76,75 | 73,625 | 0,73344652 | |||
| 81,75 | 79,25 | 1,123028391 | |||
| 84,375 | 1,232592593 | ||||
| 91,25 | 89,125 | 0,897615708 | |||
| 97,25 | 94,25 | 0,795755968 | |||
| 77,25 | |||||
Полученные значения занесем в таблицу 5.2.6:
Таблица 5.2.6
| квартал1 | квартал2 | квартал3 | квартал4 | |
| - | - | 1,2444 | 1,3894 | |
| 0,8665 | 0,6467 | 1,1649 | 1,1256 | |
| 0,8839 | 0,7334 | 1,123 | 1,2326 | |
| 0,8976 | 0,7958 | - | - | |
| среднее | 0,88267 | 0,7253 | 1,177433 | 1,2492 |
Определим корректирующий множитель. Он равен отношению 4 к сумме вычисленных индексов:
4/(0,88267+0,7253+1,177433+1,2492) =0,991423444.
На корректирующий множитель умножается значение каждого из четырех квартальных индексов. Сумма скорректированных индексов должна быть равна числу периодов сезонности (в данном примере числу кварталов). В данном примере скорректированные индексы следующие:
S1 = 0,88267* 0,99142= 0,875097;
S2 = 0,7253* 0,99142= 0,71908;
S3 = 1,177433* 0,99142= 1,167336;
S4 = 1,2492* 0,99142= 1,238487;
Шаг 3 .Десезонализированные данные вычисляются как отношение фактических уровней временного ряда к соответствующему индексу сезонности:
dt = yt/St ;
Вычислим десезонализированные данные (Таблица 5.2.7):
Таблица 5.2.7
| yt | St | dt |
| 0,875097 | 25,14007 | |
| 0,71908 | 19,46932 | |
| 1,167336 | 41,97592 | |
| 1,238487 | 50,06108 | |
| 0,875097 | 49,13741 | |
| 0,71908 | 48,6733 | |
| 1,167336 | 58,25229 | |
| 1,238487 | 63,78751 | |
| 0,875097 | 68,56383 | |
| 0,71908 | 75,09596 | |
| 1,167336 | 76,24197 | |
| 1,238487 | 83,97343 | |
| 0,875097 | 91,41844 | |
| 0,71908 | 104,2999 | |
| 1,167336 | 90,80505 | |
| 1,238487 | 103,3519 |
Шаг 4. По десезонализированным данным строится тренд, как уравнение парной регрессии, где 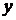 -зависимая переменная, а
-зависимая переменная, а 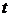 – объясняющий фактор. Линейный тренд в данном примере имеет вид:
– объясняющий фактор. Линейный тренд в данном примере имеет вид:
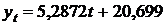 ;
;
3) Выполним прогноз на первый квартал 2014 года по аддитивной модели:
t = 17;
S1=-7,91667;
ŷ17=(23,621+5,0691*17)-7,91667=108,879 (млн. киловатт в час).
Выполним прогноз на первый квартал 2014 года по мультипликативной модели:
t = 17;
Коэффициент сезонности: S1 = 0,875097;
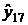 = (5,2872*17 + 20,699)*0,875097 = 94,0938(млн. киловатт в час).
= (5,2872*17 + 20,699)*0,875097 = 94,0938(млн. киловатт в час).
Варианты индивидуальных заданий к лабораторной работе №4
Задание. Имеются поквартальные данные об объемах потребления электроэнергии жителям региона за 4 года (Таблица 5.3.1).
Таблица 5.3.1
| Год | Квартал 1 | Квартал 2 | Квартал 3 | Квартал 4 |
| 22+2N | 14+2N | 49+2N | 62+2N | |
| 43+3N | 35+3N | 68+3N | 79+3N | |
| 60+4N | 54+4N | 89+4N | 104+4N | |
| 79+5N | 75+5N | 106+5N | 128+5N |
Требуется: построить аддитивную модель и мультипликативную модели и выполнить прогноз потребления электроэнергии на N кварталов вперед. N- номер варианта.
|
из
5.00
|
Обсуждение в статье: АДДИТИВНАЯ И МУЛЬТИПЛИКАТИВНАЯ МОДЕЛИ ВРЕМЕННЫХ РЯДОВ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

