Основные положения квантовой механики

Обычно начало формирования современных представлений квантовой механики связывают, прежде всего, с именами де-Бройля, Шредингера, Борна и ряда других выдающихся ученых первой половины ХХ-го века. Если не касаться тех сторон первоначальной теории, которые в настоящее время имеют лишь историческое значение, то основная мысль де-Бройля (1923 г.) заключалась в распространении основных законов квантовой теории света на движение частиц.

В первую очередь, с движением всякой свободно движущейся частицы, имеющей энергию Е и импульс р, де Бройль связывает плоскую волну

 

r, t) = C·exp[ - i(ωt –kr)],

где r– радиус-вектор произвольной точки пространства, t – время. Частота этой волны ω и ее волновой вектор k связаны с энергией и импульсом частицы p= mv (m –масса частицы, v –вектор ее скорости)теми же уравнениями, которые справедливы и для квантов света (фотонов), т.е.

E = 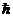ω

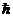p = k

Здесь = 1,05·10 ^-34 Дж·с представляет т.н. постоянную Планка, введенную последним при формулировании начальных положений квантовой теории излучения. Строго говоря, сам Планк в качестве своей постоянной ввел значение h = 2π 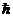= 6,6·10 ^-34 Дж·с, которую можно связать с длиной волны выражением

λ = h / p

Однако сегодня использование в качестве постоянной Планка значения 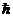считается более удобным, т.к. позволяет в большинстве случаев компактнее записывать основные соотношения и уравнения квантовой механики. Тем не менее, при дальнейшем изложении в ряде случаев будет использоваться и постоянная Планка h в ее исходном значении.

Возвращаясь к гипотезе де-Бройля, отметим, что сам он не дал развернутого физического истолкования введенной волны, но и в такой форме она оказалась приемлемой для интерпретации дифракции электронов на пространственных решетках монокристаллов. Соответствующие эксперименты, проведенные в 1927 г. американскими физиками Дэвиссоном и Джермером, полностью подтвердили высказанную гипотезу. С этого момента начинается интенсивное развитие квантовой (или, как иногда ее называют, волновой) механики, а сама волна де-Бройля по-прежнему остается и фундаментальным понятием, и своеобразным рабочим инструментом при соответствующих квантовомеханических расчетах и интерпретации их результатов.

Поскольку нашей задачей является описание с квантовомеханической точки зрения движения микрочастиц, в совокупности составляющих твердое тело, то здесь нет необходимости учитывать релятивистские эффекты, т.к. тепловые скорости микрочастиц в твердом теле заведомо много меньше скорости света. В этом смысле другим важнейшим элементом квантовой механики является уравнение Шредингера, которое играет в ней такую же роль, как уравнения (законы) Ньютона в классической физике.

Австрийский физик Шредингер предложил рассмотреть вид волновой функции Ψ, первоначально введенной де Бройлем только для свободной частицы, в произвольных силовых полях U(r,t) и, в конечном итоге, постулировал некоторое фундаментальное соотношение для функции Ψ(r, t) и ее производных в качестве основного уравнения нерелятивистской квантовой механики. Справедливость данного постулата (как и всяких постулатов) подтверждается согласием с опытом получаемых с его помощью результатов.

Уравнение Шредингера (нерелятивистское) с учетом ранее введенных выражений имеет вид

 

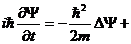U(r,t)

где 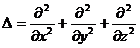- т.н. оператор Лапласа. Это уравнение часто называют временным уравнением Шредингера. Однако, если силовое поле, в котором движется частица, стационарно, т.е. функция U = U(r) не зависит от времени и имеет тогда смысл потенциальной энергии, то решение временного уравнения можно искать в виде произведения двух функций, одна из которых ψ(r) есть функция только координат, а другая φ(t) - только времени. В этом случае, как легко показать, исходное уравнение распадается на два уравнения, причем константу разделения в достаточно стандартной процедуре обозначаем через Е:

 

 

(r) + U(r)· (r) = E (r)

 

Последнее уравнение из этих двух называют стационарным уравнением Шредингера, и оно в дальнейшем изложении будет играть основную роль.

В квантовой механике используется соответствие между измеряемыми физическими величинами (L– векторными, L_x – невекторными) и т.н. операторами векторными и, соответственно, 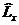невекторными. Здесь под оператором понимается некоторая совокупность (алгоритм) математических действий над исходной функцией, приводящая к получению другой функции. Оказывается, что в квантовой механике представляют интерес только операторы с определенными свойствами (т.н. эрмитовы операторы), которые, в частности, удовлетворяют специальному типу операторных уравнений (как правило, в частных производных), а именно:

 

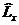ψ = L_x∙ψ

 

Если подобное уравнение (при заданных граничных условиях) имеет решение в виде некоторой функции ψ, то последняя называется собственной функцией оператора или 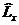, а L и L_x называется собственным значением оператора соответствующего оператора (при заданных условиях). Важно отметить, что в экспериментах по определению конкретной физической величины (импульса, энергии, координаты и т.п.) могут получаться только значения, равные собственным значениям соответствующего оператора.

Теперь очевидно, что в вышеприведенном стационарном уравнении Шредингера константа разделения Е представляет полную энергию частицы, т.к. является собственным значением оператора энергии

,

который называется «гамильтониан»

 

Решая первое уравнение, получаем выражение для временной функции в виде

 

 

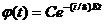
где С – произвольная постоянная. Таким образом, в случае стационарного силового поля состояние частицы описывается волновой функцией

 

Ψ(r, t) = ψ(r)·exp(- iEt/ )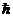

 

Здесь постоянная С включена в функцию ψ(r). Отсюда следует, что стационарность состояния не исключает зависимости волновой функции от времени, а только ограничивает ее гармоническим законом exp(- iEt/ 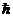) = exp(-iωt). В частном случае свободного движения частицы (U = 0) волновая функция, как легко видеть, переходит в плоскую волну де Бройля.

Интересно, что правильное толкование физического смысла волновой функции дал не Шредингер, а немецкий ученый М.Борн. Согласно Борну, волновые функции Ψ должны интерпретироваться статистически. При этом физический смысл (т.е. утверждение, соответствующее возможности проверке в эксперименте) имеет только квадрат модуля волновой функции, а именно,

| Ψ|² = Ψ* Ψ ,

 

который интерпретируется как плотность вероятности, т.к. определяет вероятность dW нахождения частицы в момент времени t в объемной окрестности dV данной точки пространства r, а именно

dW = | Ψ|² dV

Нетрудно показать, что в стационарном состоянии плотность вероятности | Ψ|² = |ψ|² выражается только через ψ(r) и не зависит от времени. Общепринято ψ(r) также называть волновой функцией, хотя она является только координатной частью полной волновой функции Ψ (r, t) стационарного состояния.

В стационарное уравнение Шредингера в качестве параметра входит полная энергия Е частицы. С точки зрения математики, такие уравнения имеют бесчисленное множество решений. Из них посредством наложения определенных условий отбирают решения, имеющие физический смысл. Для уравнения Шредингера такими условиями являются условия регулярности волновых функций: волновые функции вместе со своими первыми производными должны быть конечными, однозначными и непрерывными. Однако регулярные решения имеют место не при любых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи (точнее, для данного вида U(r), т.е. профиля потенциальной энергии). Эти значения энергии, как уже было сказано, называют собственными. Решения, которые соответствуют собственным значениям энергии, называются собственными функциями. Собственные значения Е могут, в принципе, иметь как непрерывный, так и дискретный спектр значений. В частности, волны де Бройля в безграничном пространстве соответствуют непрерывному энергетическому спектру, а вот любая локализация частицы в пространстве приводит к квантованию ее энергетического спектра.

Состояние, отвечающее волновой функции с наименьшим возможным значением энергии, называется основным состоянием.

Учет волновых характеристик движения микрочастиц и вероятностная интерпретация волновых функций приводят к необходимости введения в рассмотрение т.н. неравенств Гейзенберга:

Δx∙Δp_x ≥ h

Δy∙Δp_y ≥ h

Δz∙Δp_z ≥ h

ΔE∙Δt ≥ h

В дальнейшем нас будут интересовать, в первую очередь, волновые функции, описывающие возможные состояния электрона в металле. При этом каждое конкретное состояние может быть занято электроном или остаться свободным. Степень заполнения состояния (т.е. количество электронов в данном состоянии) определяется статистическим распределением Ферми-Дирака, учитывающим, среди прочего, известный принцип Паули, а именно, в одном квантовом состоянии может находиться не более двух электронов, отличающихся противоположными направлениями проекций спинов на заданную выделенную ось. Иногда спиновое число рассматривают как дополнительное квантовое число, определяющее конкретную функцию состояния; тогда в этом состоянии может находиться или только один электрон, или ни одного.

Теория Зоммерфельда

 

Теория Зоммерфельда сохраняет все основные предпосылки теории Друде в отношении газа электронов в металле (т.е. свободные и независимые электроны), только вместо классического газокинетического (максвелловского) распределения электронов по энергиям принимается распределение Ферми-Дирака.

Для простоты изложения мы сначала рассмотрим свойства электронного газа в основном состоянии (т.е. при температуре Т = 0), а затем уже перейдем к изучению отличных от нуля температур. Оказывается, такой подход представляет и самостоятельный интерес: далее будет показано, что для электронов комнатная температура очень мала, и поэтому многие (но не все!) физические параметры, характеризующие электронные свойства металлов, определяются состоянием электронного газа при нулевой температуре.

Итак, необходимо рассчитать свойства основного состояния системы из N электронов, заключенных в объеме V. Поскольку электроны (электрически!!) не взаимодействуют друг с другом, основное состояние всей этой системы можно найти, определив вначале возможные состояния отдельного (независимого!!) электрона, т.е. рассчитав все волновые функции и соответствующие уровни энергии отдельного электрона в объеме V (такие состояния отдельного независимого электрона иногда называют орбиталями). Затем необходимо заполнить электронами эти уровни снизу вверх по энергии с учетом принципа Паули (в одном состоянии из-за спинового взаимодействия не может быть больше одного электрона с заданным спином), получить чтобы состояние системы из N независимых электронов с наименьшим возможным значением их суммарной энергии.

В отсутствие взаимодействия одноэлектронная волновая функция, соответствующая уровню энергии Е, удовлетворяет стационарному уравнению Шредингера,

(r) + U(r)· (r) = E (r)

где можно положить значение U(r) = 0 (свободный электрон!). Тогда имеем следующее дифференциальное уравнение:

(r) = E (r)

Чтобы учесть, что движение электрона ограничено объемом V металла, необходимо ввести граничные условия, которым должно удовлетворять решение последнего уравнения. В задачах, не связанных с рассмотрением поверхностных явлений, выбор такого граничного условия остается в значительной мере произвольным и обычно производится исходя из удобства дальнейших вычислений.

Естественно ожидать, что при достаточно больших размерах образца металла, его объемные свойства не будут зависеть от детальных характеристик формы и поверхности. Поэтому можно выбрать форму образца в виде куба со стороной L = V ^1/3.

Теперь выберем конкретные граничные условия, отражающие тот факт, что электрон удерживается внутри выбранного куба. Кроме того, эти условия не должны влиять на объемные свойства. Здесь могут быть два пути. Первый, очень часто используемый в некоторых модельных задачах, состоит в том, чтобы положить значения функции (r)= 0 на границах куба. Однако это приводит к решениям в виде стоячих волн, что в нашем случае не совсем удобно, т.к. перенос заряда и энергии целесообразнее анализировать на основе бегущих волн. Более адекватным, следовательно, является второй путь, позволяющий вообще отказаться от поверхности, подчеркнув, тем самым еще раз, отсутствие ее влияния на процессы переноса. Это можно сделать, представив, что каждая из граней куба соединена с противоположной ей гранью: тогда электрон, подходящий к поверхности, не отражается обратно, а выходит из металла и одновременно входит в него в соответствующей точке противоположной грани. Если бы образец металла был одномерным, то это означало, что отрезок прямой L, где содержатся электроны, заменялся бы окружностью длиной L. В трехмерном случае подобная манипуляция, конечно, топологически неосуществима, но аналитически запись соответствующих граничных условий возможна в следующем виде:

 

(x+L, y, z) = (x, y, z)

(x, y+L, z) = (x, y, z)

(x, y, z+L) = (x, y, z)

 

Эти соотношения называют граничными условиями Борна-Кармана, или периодическими граничными условиями. Они очень часто используются в различных задачах квантовой механики.

Теперь займемся решением уравнения Шредингера. Как нетрудно убедиться прямой подстановкой, общим решением этого стационарного уравнения является функция вида

_k(r) =

При этом энергия электрона выражается как E(k) = , где k – любой вектор, не зависящий от пространственных координат.

В представленной записи волновой функции нормировочный множитель выбран так, чтобы вероятность нахождения электрона где-либо в объеме V была равна единице, т.е. интеграл по всему объему от квадрата модуля функции равен единице:

 

∫ | |²dr = 1

 

Чтобы понять смысл вектора k, заметим, что волновая функция _k(r) представляет собой собственную функцию оператора импульса :

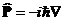(соответственно, 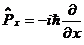и т.д.),

определяющую собственное значение импульса p = ћk, т.к.

 

^ikr= ћk∙e^ikr

Если, как уже было неоднократно подчеркнуто, состояние частицы описывается волновой функцией, являющейся собственной функцией какого-либо оператора, то соответствующая наблюдаемая (физическая величина!) имеет в этом состоянии определенное значение, равное собственному значению оператора. Поэтому электрон с волновой функцией _k(r)обладает определенным импульсом p= ћkи, соответственно, скоростью v = p/m = ћk / m

 

С учетом этого можно записать его энергию в привычном классическом виде:

 

 

Очевидно, что энергия Е сама является собственным значением оператора энергии в уравнении Шредингера (при отсутствии силового поля U).

 

Величину k можно интерпретировать как волновой вектор, причем его модуль (называемый волновым числом) равен k = 2π/λ, а всю функцию _k(r) = (с учетом временной части общей функции Ψ). можно рассматривать как бегущую плоскую волну с длиной волны λ. Другими словами, это есть уже знакомая нам волна де Бройля.

Теперь надо воспользоваться вышеуказанными граничными условиями, чтобы отобрать из всего множества волн де Бройля только физически возможные. Как легко видеть, они допускают существование только дискретных значений k, поскольку волновая функция удовлетворяет граничным условиям только при выполнении условий

 

exp(ik_xL) = exp(ik_yL) = exp(ik_zL) = 1

 

Поскольку данное равенство возможно только при равенстве степени всех экспонент i2πn, где n – целое число (положительное, отрицательное или нуль), можно заключить, что компоненты волнового вектора k должны иметь вид:

 

,

где n_x , n_y , n_z – целые числа (0, ±1, ±2, ±3,…..). Иногда их называют квантовыми числами соответствующего квантового состояния..

Таким образом, компоненты импульса электрона могут принимать только дискретные значения:

p_x =2π ћn_x /L = hn_x /L

p_x =2π ћn_y /L = hn_y /L

p_x =2π ћn_z /L = hn_z /L

 

 

Ясно, что возможные уровни энергии электрона могут быть выражены через те же квантовые числа, а именно:

 

Из этого выражения видно, что уровни энергии вырождены, т.к. одному и тому же конкретному значению энергии соответствуют разные тройки целых чисел n_x , n_y , n_z, определяющих разные состояния электрона (разные _k(r), разные вектора k, хотя и с одинаковым модулем).

Для дальнейшего рассмотрения необходимо ввести понятие т.н. фазового пространства, широко используемого во многих разделах физики. в т.ч. в квантовой механике. Это пространство (в случае одной частицы) определяется тремя координатными осями X, Y, Z и тремя осями, соответствующими проекциям импульса на координатные импульсы. Иногда для удобства анализа рассматривают отдельно импульсную и/или координатную части этого фазового пространства. Заметим, что в ряде монографий и учебников для обозначения фазового пространства используется термин Г-пространство или μ-пространство.

В нашем случае кубического образца металла очевидно, что доступная координатная часть фазового пространства ограничена объемом V=L³. Рассмотрим импульсную часть фазового пространства. Возможные значения каждой тройки проекций импульсов будут изображаться точками в трехмерном импульсном пространстве, причем ближайшие расстояния между этими точками равны h/L. Можно считать, что на каждую точку (т.е. на каждое состояние ψ) приходится в импульсном пространстве объем h³/L³ = h³/V, а во всем фазовом пространстве (с учетом координатного пространства объемом V) каждое возможное разрешенное квантовое состояние занимает объем h³.Этот результат чрезвычайно важен и имеет общий характер в квантовой физике. Мы еще будем неоднократно его использовать при практических расчетах и оценках применительно к модели свободных электронов, где энергия и импульс электрона связаны простым соотношением E = p²/2m.

Статистика фермионов

В предыдущем разделе рассмотрены возможные энергетические состояния электронов в кристаллических телах. При этом допустимый уровень может быть или заполнен электроном, или оставаться пустым. Поэтому самостоятельный интерес представляет реальное распределение электронов по допустимым уровням энергии.

Ответ на поставленный вопрос дает статистическая физика, изучающая, в частности, равновесное распределение микрочастиц по различным квантовым состояниям. Применительно к электронам важнейшим фактором служит то, что они является т.н. фермионами, подчиняющимися статистике Ферми-Дирака. Признаком фермионов является выражение их спина (собственного механического момента, т.е. момента импульса) через нецелочисленное число s, кратного ½, причем число кратности – нечетное. Это является кратким физическим выражением того факта, что модуль спина фермиона равен M = .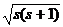

Применительно к электрону заметим, что его спин выражается через спиновое число s = ½ (т.е. вышеупомянутое число кратности – единица). Иногда для краткости говорят просто, что спин электронов равен ½ , а его проекция на любое выделенное (например, магнитным полем) направление Z равна М_z = ± s .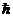

Так как электрон является заряженной частицей, то наличие механического момента обуславливает и существование магнитного момента электрона, ориентированного соосно с механическим моментом, но в противоположном направлении (из-за отрицательного заряда электрона). Оказывается, что т.н. спиновое взаимодействие приводит к тому, что фермионы могут занимать какой-либо энергетический уровень только поодиночке или попарно, причем в последнем случае спины электронов направлены в противоположные стороны (вышеупомянутый принцип Паули).

В дальнейшем будем использовать для каждого направления проекции спина свою функцию Ферми-Дирака, которая фактически выражает вероятность заполнения электронами любого энергетического уровня Е в зависимости от температуры Т. В этом случае она имеет вид

 

 

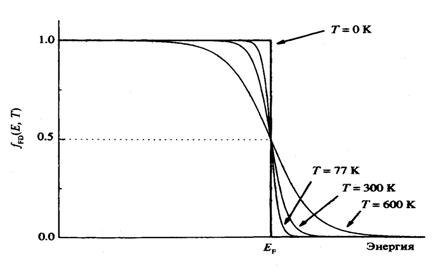
Рис. 2-1. Функция Ферми-Дирака при разных температурах Т..

 

 

График этой функции отражен на рис. 2-1. Имеющий размерность энергии параметр E_Fназывают уровнем Ферми. Этот параметр появляется при выводе формулы Ферми-Дирака, например, из статистического распределения Гиббса, где он имеет изначальный физический смысл как химический потенциал µ, соответствующий приращению или убыли энергии статистической системы при появлении или убыли в ней одной частицы (например, при обмене частицами с другими системами). Можно показать, что в твердом теле химический потенциал µ сравнительно слабо зависит от температуры. Поэтому значение µпри Т = 0 в физике твердого тела традиционно обозначается как E_F , являющегося при Т = 0 своеобразной границей между заполненными и пустыми разрешенными энергетическими уровнями. Действительно, элементарный анализ функции f(E) показывает, что при Т = 0 график функции имеет вид ступеньки с высотой 1, оканчивающейся на уровне Ферми (см. рис. 2-1). Другими словами, при температуре абсолютного нуля все разрешенные уровни до E_Fзаполнены с вероятностью 1. При температуре, большей абсолютного нуля, ступенька размывается в обе стороны, причем ширина этого размытия, как показывает оценка, порядка kT.

Очевидно, что в пространстве волновых векторов (в k-пространстве) каждое разрешенное состояние будет занимать объем (2π)³/V и определяется набором дискретных квантовых чисел k_x, k_y, k_z . Энергия Ферми E_Fпри Т = 0 соответствует совокупности волновых векторов kс максимальным модулем k_{max .} Заметим, что соотношение Е = ћ² k² / 2m выполняется только для волновых функций типа волн де Бройля.

На рис. 2-2 изображена только одна верхняя четверть k-пространства, т.е. один октет полного пространства. Выделенная сфера толщиной dk содержит общее число G(k)dk электронных состояний в любом промежутке значений (k, k+dk), которое, с учетом принципа Паули, можно выразить следующим выражением:

G (k)dk= 2∙ ,

где G(k) можно рассматривать как плотность состояний по волновому числу k во всем объеме V кристалла. Коэффициент 2 в правой части равенства учитывает электроны с противоположными спинами. Тогда, соответственно, плотность числа состояний N(k) в k-пространстве, приходящаяся на единицу координатного объема, может быть выражена в следующем виде:

 

N(k)dk =

 

Отсюда, используя соотношение E = ћ²k²/2m и считая, что интервал dk соответствует определенному интервалу dE, легко получить функцию распределения плотности состояний по энергии g(E), отнесенную к единице объема металлического кристалла, а именно:

 

k² = 2mE/ ћ²; k = (2mE)^1/2/ ћ; dk = ;

N(k)dk = g(E)dE;

 

 

Рис. 2-2. Четверть верхнего сферического слоя (октет) в k-пространстве, соответствующая энергиям частиц

в диапазоне (E, E+dE)

 

Умножив g(E) на функцию Ферми-Дирака f_FD(E), получаем функцию распределения по энергии F(E) в окончательном виде, показанном на рис. 2-3. Очевидно, что при 0 К заняты лишь все состояния до E_F, а при Т > 0 некоторые из электронов начинают заполнять уровни выше E_F.

Рис. 2-3. Плотность заполненных электронных состояний как функция энергии Е. Для наглядности нарушен масштаб по горизонтали: при заданном размытии энергетического спектра в окрестности E_F надо было бы растянуть остальную часть графика по горизонтали, примерно, в 200 раз (при комнатной температуре).

 

Воспользовавшись полученными результатами, можно попытаться вычислить значение энергии Ферми. Легче всего это сделать для случая Т = 0, где функция Ферми-Дирака f_FD(E) везде равна единице, т.е. здесь все уровни заполнены до E_F. Кроме того, необходимо знание численного значения концентрации электронов n_e в металле. Таким образом, получаем следующее уравнение, в котором процедура интегрирования не вызывает проблем:

 

=

 

Для типичного значения концентрации электронов в металле n_e ≈ 10²³ см^-3 = 10²⁹ м^-3 оценка уровня Ферми в металлах соответствует энергии, примерно, 5 эВ. Это позволяет формально ввести т.н. температуру Ферми T_F = E_F / k_B, которая в этом случае равна порядка 60 000 К, т.е. в 200 раз превышает комнатную температуру. Таким образом, даже при температуре абсолютного нуля электроны уже имеют среднюю энергию в несколько эВ, в десятки раз превышающую энергию, соответствующую комнатной температуре (~ 0,025 эВ). Доля валентных электронов, реально увеличивающих свою энергию при нагреве, определяется их ничтожной частью в зоне размытия вблизи энергии E_{F .} Это и является главной причиной, почему электроны не дают практически никакого вклада в теплоемкость твердого тела в широком диапазоне температур (только при температуре в несколько кельвинов их вклад становится соизмеримым с теплоемкостью собственно кристаллической решетки, которая, как будет показана дальше, при низких температурах пропорциональна Т ³ ).

Если рассмотреть в импульсной части фазового пространства совокупное положение всех состояний с уровнем Ферми E_{F ,} то при большом числе электронов N оно будет соответствовать сфере с радиусом . Ее часто называют поверхностью Ферми. Иногда поверхность Ферми определяется в пространстве волновых векторов k(k_x, k_y, k_z). В общем случае, при более реальном учете возможной неизотропности внутренней структуры кристалла эта поверхность может быть и несферической формы.