Определяем точность найденных диаметров по межосевому расстоянию

 

                                                                                   (3.11)

 

мм

Таким образом, найденные диаметры определены, верно.

Определяем силы в зацеплении:

Окружная сила направлена по касательной в точки касания колеса и шестерни.

 

 (3.12)

 

где Т₂ - вращающий момент на 2 промежуточном валу, Н·м;

d₂ – делительный диаметр шестерни, мм.

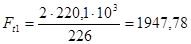 Н

Радиальная сила направлена к центру окружности и определяется по формуле (с.19 [2]) :

                   (3.13)

где F_t – окружная сила, Н;

α – между геометрической суммой радиальной и осевой силами,

β- угол наклона зубьев, tg β=0,364.

 Н

Проверяем зубья колес по напряжениям изгиба. Должно выполняться неравенство

Для колеса

 

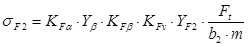
(3.14)

 

где 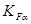- коэффициент, учитывающий распределение нагрузки между зубьями. (с.15 [2]), 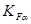=0,91;

- коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (с.16 [2]), 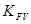=1,4;

- коэффициент неравномерности нагрузки по длине зуба (с.16 [2]),

=1,25;

- коэффициент, учитывающий наклон зуба,

 

= ;

 

- коэффициенты формы зуба шестерни и колеса (с.16 [2]), =3,61;

b₂ - ширина колеса, мм.

 Мпа

Для шестерни

 

                                                                                (3.15)

 

где    - коэффициенты формы зуба шестерни и колеса (с.16 [2]), 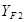=3,61;

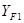- коэффициенты формы зуба шестерни и колеса (с.16 [2]), =3,92;

- напряжение изгиба на колесе, Мпа.

 Мпа

Так как [σ]_F1=547,83 МПа, [σ]_F2=495,65 МПа и σ_F1=390,5 МПа, σ_F2=359,91 МПа, что удовлетворяет условию [σ]_F1  σ_F1 , [σ]_F2  σ_F2 то колеса прошли проверку по напряжениям на изгиб.

Проверяем зубья колес по контактным напряжениям .

 

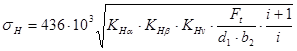                                          (3.18)

 

где , , -коэффициенты учитывающие распределение нагрузки между зубьями, неравномерность распределения нагрузки по длине контактной линии, дополнительные динамические нагрузки, так как редуктор рассчитан на долгий срок службы то =1, =1, =1.

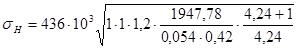=498,41 МПа

Определяем, погрешность допускаемого напряжения

 

% (3.19)

 

%=0,5%

Колеса перегружены на 0,5%.

 

Вывод

 

При определении погрешности передаточного числа, получили Δi= 1,4% , что позволяет сделать вывод- передаточное число выбрано, верно.

Так как [σ]_F1=547,83 МПа, [σ]_F2=495,65 МПа и σ_F1=390,5 МПа, σ_F2=359,91 МПа то колеса прошли проверку по напряжениям на изгиб.

В результате расчетов определили, что 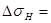0,5% перегрузки. Это величина не превышает допустимого значения (5 % перегрузки и 10 % недогрузки), следовательно, колеса прошли проверку по контактным напряжениям.

    В результате проверочного расчета убедились, что полусумма делительных диаметров равна межосевому расстоянию.

 

Расчет тихоходной прямозубой цилиндрической зубчатой передачи

 

Задача

 

Провести проектный расчет, подобрать материал, определить основные геометрические параметры и проверить на контакт.

 

Расчетная схема

 

 

Рисунок 4.1 – Расчетная схема зацепления колес

Данные для расчета

Данные для расчета передачи берем из кинематического расчета.

 

Таблица 3.1 - силовые и скоростные параметры для расчета промежуточной передачи

/Параметр	Р, кВт	Т, Н·м	ω, с-1	n , об/мин	i
3 вал	6,312	220,1	28,68	274	3,3
4 вал	6,06	697,4	8,69	83

 

Условие расчета

 

Проектный расчет ведем на контакт, так как основной вид разрушения закрытых зубчатых передач - поверхностное выкрашивание зубьев в зоне контакта. Проверяем на контакт и изгиб.