 |
Главная |
Оптимальное смешивание
|
из
5.00
|
ВАРИАНТ 3
ЭКОНОМИЧЕСКИЕ СИТУАЦИИ, РАЗРЕШАЕМЫЕ МЕТОДАМИ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ В ЭКОНОМИКЕ
Основные экономические ситуации, разрешаемые методами исследования операций, предполагают решение следующих задач:
Оптимизация плана производства
Общая постановка задачи планирования производства: необходимо определить план производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материальных, финансовых и других видов ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия — максимума прибыли, минимума затрат на производство и т.д.
Введем обозначения:
п — количество выпускаемых продуктов;
т — количество используемых производственных ресурсов (например, производственные мощности, сырье, трудовые ресурсы);
а ij — объем затрат i -го ресурса на выпуск единицы j-й продукции;
сj — прибыль от выпуска и реализации единицы j-го продукта;
bi — количество имеющегося i-го ресурса;
х j — объем выпуска j-го продукта.
Задача оптимизации производственной программы может быть описана с помощью следующеймодели линейного программирования:
 (1)
(1)
 (2)
(2)
 (3)
(3)
Здесь (1) — целевая функция (максимум прибыли);
(2) — система специальных ограничений на объем фактически имеющихся ресурсов;
(3) — система общих ограничений (не отрицательность переменных);
х j — переменная.
Задача (1)—(3) называется задачей линейного программирования в стандартной форме на максимум. Задача линейного программирования в стандартной форме на минимум имеет вид:
 (4)
(4)
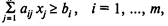 (5)
(5)
 (6)
(6)
Вектор х = (x1, x2, ..., xn), компоненты х j которого удовлетворяют ограничениям (2) и (3) (или (5) и (6) в задаче на минимум), называется допустимым решением или допустимым планом задачи. Совокупность всех допустимых планов называется множеством допустимых планов.
Допустимое решение задачи линейного программирования, на котором целевая функция (1) (или (3) в задаче на минимум) достигает максимального (или минимального) значения, называется оптимальным решением задачи линейного программирования.
Оптимальное смешивание
Важный класс прикладных оптимизационных задач образуют задачи о смесях. Такие задачи возникают при выборе наилучшего способа смешения исходных ингредиентов для получения смеси с заданными свойствами. Смесь должна иметь требуемые свойства, которые определяются количеством компонентов, входящих в состав исходных ингредиентов. Как правило, известны стоимостные характеристики ингредиентов и искомую смесь требуется получить с наименьшими затратами. Для многопродуктовых задач, в которых требуется получить несколько смесей, характерным является критерий максимизации прибыли.
Задачи оптимального смешения встречаются во многих отраслях промышленности (металлургия, парфюмерия, пищевая промышленность, фармакология, сельское хозяйство). Задачи о смесях: определение кормового рациона скота на животноводческих фермах, составление рецептуры шихты в металлургическом производстве и т.п.
Однопродуктовые модели оптимального смешения. Введем обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси;
х j — количество j-го ингредиента, входящего в смесь;
а ij —количество i-го компонента в j-м ингредиенте;
с j —стоимость единицы j-го ингредиента;
bi — количество i-го компонента всмеси.


Здесь (1) — целевая функция (минимум затрат на получение смеси);
(2)— группа ограничений, определяющих содержание компонентов в смеси;
(3) — ограничения не отрицательности переменных.
В задаче могут присутствовать также ограничения на общий объем смеси и ограничения на количество используемых ингредиентов. Эти группы ограничений, а также ограничения (2) характерны для задачи планирования производства. Применяются обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси;
w — количество условий, отражающих содержание j-го ингредиента в смеси;
х j — количество j-го ингредиента, входящего в смесь;
а ij — доля j-го компонента в j-м ингредиенте;
bi — минимально допустимая доля i-го компонента в смеси;
с j — стоимость единицы j-го ингредиента;
drj — коэффициент, отражающий r-е условие на содержание j-го ингредиента в смеси.


Здесь (4) — целевая функция (минимум затрат на получение смеси);
(5) — группа ограничений, определяющих содержание компонентов в смеси;
(6) — группа ограничений на содержание ингредиентов в смеси;
(7) — ограничение на количество смеси;
(8) — ограничения не отрицательности переменных.
Ограничения (5) и (6) отличают задачу смешения от задачи оптимального планирования производства. Значения правых частей этих ограничений равны нулю. Вектор х* с компонентами, являющийся решением этой оптимизационной задачи, называют рецептом приготовления смеси или рецептом смешения. В многопродуктовых задачах ингредиенты используются для приготовления не одной, а нескольких смесей. При этом в качестве переменной xkj, такой задачи рассматривается количество ингредиента j, используемое для приготовления смеси k. Критерий задачи — максимизация прибыли.
Оптимальный раскрой
Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала.Задача оптимального раскроя состоит в том, чтобы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. Задачи такого типа возникают в металлургии и машиностроении, лесной, лесообрабатывающей, легкой промышленности. Выделяют два этапа решения задачи оптимального раскроя. На первом этапе определяются рациональные способы раскроя материала, на втором — решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.
В задачах оптимального раскроя рассматриваются рациональные (оптимальные по Парето) способы раскроя. Например, из единицы материала можно изготовить заготовки нескольких видов. Способ раскроя единицы материала называется рациональным (оптимальным по Парето), если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.
Пусть k — индекс вида заготовки, k = 1,.... q; i — индекс способа раскроя единицы материала, i = 1,..., р; а ik — количество (целое число) заготовок вида k , полученных при раскрое единицы материала i -м способом. Приведенное определение рационального способа раскроя может быть формализовано следующим образом. Способ раскроя v называетсярациональным (оптимальным по Парето), если для любого другого способа раскроя i из соотношений а ik ³ а vk , k = 1, ..., q , следуют соотношения а ik = а vk , k = 1, ..., q .
Определение интенсивности использования рациональных способов раскроя. Обозначения:
j —индекс материала, j = 1,..., п ;
k —индекс вида заготовки, k = 1, ..., q ;
i — индекс способа раскроя единицы материала, i = 1,..., р ;
а ijk — количество (целое число) заготовок вида k , полученных при раскрое единицы j-го материала i-м способом;
bk — число заготовок вида k в комплекте, поставляемом заказчику;
dj — количество материала j-го вида;
xji — количество единицу j-го материала, раскраиваемых по i-му способу (интенсивность использования способа раскроя);
cji — величина отхода, полученного при раскрое единицы j-го материала по i-му способу;
у — число комплектов заготовок различного вида, поставляемых заказчику.
Раскрой с минимальным расходом материалов:

Здесь (1) — целевая функция (минимум количества используемых материалов);
(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(3) — условия не отрицательности переменных.
Раскрой с минимальными отходами:


Здесь (4) — целевая функция (минимум отходов при раскрое материалов);
(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;
(6) — условия не отрицательности переменных.
Планирование финансов
Минимизации целевого фонда. Например, в определенные моменты времени необходимо выплачивать известные суммы денег по взятому ранее займу. Чтобы накопить эти суммы, можно заранее создать целевой фонд, а средства из этого фонда использовать для срочных вкладов. Каждый срочный вклад характеризуется моментом времени вложения, сроком погашения и доходностью. Задача состоит в том, чтобы определить минимальный размер целевого фонда и выбрать те виды срочных вкладов, которые следует использовать, чтобы сделать выплату по займу. Обозначения:
у — размер целевого фонда, создаваемого в нулевой момент времени;
t — текущий момент времени, t = 0, 1,.... Т;
dt — размер выплаты по займу, которую надо произвести в момент времени t (t = 1, ..., Т);
j —индекс срочного вклада, j = 1,..., п ;
vj — момент времени вложения по срочному вкладу j;
wj — срок выплаты по срочному вкладу j;
rj — доходность срочного вклада j (процент по вкладу);
х j — объем вложений по срочному вкладу j.
Предполагается, что для любого срочного вклада j момент v j времени вложения фиксирован. Если по срочному вкладу сделаны вложения в размере х j, то через w j единиц времени вкладчику выплачивается сумма (1 + rj )х j. Без ограничения общности можно считать, что для любого момента времени существует такой вклад, выплата по которому производится в следующий момент времени. При этом доходность такого вклада может быть нулевая. Использование вклада с нулевой доходностью означает, что деньги остаются на руках у владельца.
Пусть Gt — множество индексов j, таких, что t= vj , т.е. по вкладу j сделано вложение в момент времени t, Qt — множество индексов j, таких, что t = vj + w j, т.е. по вкладу j получена выплата в момент времени t. Для любого t множества Gt и Qt известны.
Тогда модель имеет следующий вид:


Здесь (1) — целевая функция (минимальный размер целевого фонда);
(2) —условие, характеризующее распределение целевого фонда по вкладам в нулевой момент времени;
(3) — соотношения, устанавливающие баланс между выплатами и вложениями;
(4) — условие, обеспечивающее выплату по займу;
(5) — условия не отрицательности переменных.
Максимизация дохода. Предположим теперь, что вкладчик собирается делать вклады для того, чтобы через определенный период времени получить максимальный доход. Задача состоит в том, чтобы определить величину максимального дохода при фиксированном размере целевого фонда и выбрать те виды срочных вкладов, которые следует использовать.
Сохраним принятые ранее обозначения и введем новые:
z — размер дохода, который может получить вкладчик в момент времени Т;
и t— размер вклада в момент времени t (t = 0, 1,..., Т— 1).
Тогда модель имеет следующий вид:


Здесь (6) — целевая функция (максимальная величина дохода);
(7) — условие, характеризующее распределение вклада в нулевой момент времени;
(8) — соотношения, устанавливающие баланс между выплатами и вложениями;
(9) — условие, определяющее величину дохода;
(10) —условия не отрицательности переменных.
Транспортная задача
Известны потребности нескольких потребителей в некотором продукте. Требуется определить, от каких производителей, и в каких объемах должны получать продукт потребители. Поставки должны осуществляться таким образом, чтобы совокупные издержки на транспортировку продукта были минимальными. Обозначения:
а i — величина предложения продукта в пункте i (i = 1, ..., n);
bj — величина спроса на продукт в пункте j (j = 1,..., т);
cij — затраты на транспортировку единицы продукта из пункта i в пункт j;
xij — количество продукта, перевозимого из пункта i в пункт j.
Модель транспортной задачи:


Здесь (1) — целевая функция (минимум затрат на транспортировку продукта);
(2) — ограничения по величине предложения в каждом пункте производства;
(3) — ограничения по величине спроса в каждом пункте потребления;
(4) — условия не отрицательности объемов перевозок.
Замкнутая транспортная задача. Общее предложение равнообщему спросу:

Это необходимое и достаточное условие существования допустимого плана задачи (1)—(4).
Открытая транспортная задача.
а)  — излишек продукта
— излишек продукта
Транспортная задача с запретами. Пусть Е — множество пар индексов (ij), таких, что из пункта i в пункт j допускается транспортировка продукта. Между любыми другими двумя пунктами транспортировка не допускается.
Пусть М— большое число, например
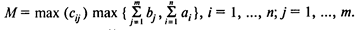
Тогда 
В оптимальном плане {  } транспортной задачи
} транспортной задачи  при ограничениях (2)—(4) xij = 0, если ( i , j) Ï Е.
при ограничениях (2)—(4) xij = 0, если ( i , j) Ï Е.
Транспортная задача с фиксированными перевозками. Если объем перевозок между пунктами i и j задан, то в задаче (1)—(4) вводится дополнительное ограничение: xij = vij, где vij — заданный объем перевозок.
Транспортная задача с ограничениями на пропускную способность. Если объем перевозок из пункта i в пункт j ограничен величиной wij, то в задаче (1)—(4) вводится дополнительное ограничение: xij £ wij .
Транспортная задача с фиксированными доплатами. В открытой транспортной задаче имеет место дефицит продукта и для его устранения в пунктах i = п + 1, ..., k возможно создание новых мощностей di .
Задача о назначениях
В процессе управления производством возникают задачи назначения исполнителей на различные виды работ, например: подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложении между различными проектами научно-технического развития, распределение экипажей самолетов между авиалиниями.
Задачу о назначениях можно сформулировать следующим образом. Необходимо выполнить N различных работ. Для их выполнения можно привлечь N рабочих. Каждый рабочий за определенную плату готов выполнить любую работу. Выполнение одной работы следует поручить одному рабочему. Требуется так распределить работы между рабочими, чтобы общие затраты на выполнение всех работ были минимальными. Пусть т — количество работ.
Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ.
Обозначения:
с ij — показатель эффективности назначения i-го рабочего на j-й работе, например издержки выполнения i-м рабочим j-й работы;
xij — переменная модели (х ij = 1, если i-й рабочий используется на j-й работе, и xij = 0 в противном случае).
Модель задачи о назначениях:


Здесь (1) — целевая функция (минимум издержек на выполнение всех работ);
(2) — система ограничений, отражающая следующие условия:
а) каждая работа должна быть выполнена одним рабочим;
б) каждый рабочий может быть привлечен к одной работе;
(3) — условия не отрицательности переменных.
При решении задачи о назначениях исходной информацией является таблица задачи о назначениях с={с ij}, элементами которой служат показатели эффективности назначений.
Результатом решения задачи о назначениях (1)—(3) является вектор х* = {  }, компоненты которого — целые числа. Оптимальный план задачи о назначениях (1)—(3) можно представить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна единица. Такую матрицу иногда называют матрицей перестановок. Значение целевой функции (1), соответствующее оптимальному плану, называют эффективностью назначений.
}, компоненты которого — целые числа. Оптимальный план задачи о назначениях (1)—(3) можно представить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна единица. Такую матрицу иногда называют матрицей перестановок. Значение целевой функции (1), соответствующее оптимальному плану, называют эффективностью назначений.
Задача о назначениях в открытой форме возникает, когда количество рабочих не равно количеству работ. В этих случаях задача может быть преобразована в задачу, сформулированную в стандартной форме. Количество рабочих п превышает количество работ т. Введем дополнительные фиктивные работы с индексами j = w + 1,..., п. Коэффициенты таблицы назначений с ij , i = 1,..., п; j = т + 1,..., п, положим равными нулю. В этом случае получаем задачу, сформулированную в стандартной форме. Если в оптимальном плане этой задачи  = 1 при j = т + 1,..., п, то исполнитель i назначается на выполнение фиктивной работы, т.е. остается без работы. Заметим, что оптимальное значение целевой функции исходной задачи совпадает с оптимальным значением задачи, приведенной к стандартной форме. Поэтому эффективность назначений в результате такого преобразования не меняется.
= 1 при j = т + 1,..., п, то исполнитель i назначается на выполнение фиктивной работы, т.е. остается без работы. Заметим, что оптимальное значение целевой функции исходной задачи совпадает с оптимальным значением задачи, приведенной к стандартной форме. Поэтому эффективность назначений в результате такого преобразования не меняется.
Задача о назначениях является частным случаем транспортной задачи, в которой количество пунктов производства совпадает с количеством пунктов потребления, а все величины спроса и величины предложения равны.
|
из
5.00
|
Обсуждение в статье: Оптимальное смешивание |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

