ЭЛЕМЕНТЫ СЕТЕВОЙ МОДЕЛИ

 

Первые системы, использующие для моделирования сетевые графики, были созданы в США в конце 50-х годов прошлого столетия. Это был метод критического пути, который использовался при управлении строительными работами и при выполнении космических проектов. В России первое применение сетевых моделей имело место в начале 60-х годов в строительстве, научных разработках и др. Сетевое планирование и управление основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчётных методов, организационных и контрольных мероприятий по исследованию, планированию и управлению комплексом работ.

Использование сетевой модели для исследования и развития операций в экономике позволяет:

- сформировать календарный план реализации некоторого комплекса работ;

- выявить и мобилизовать резервы времени, трудовые, материальные и денежные ресурсы;

- осуществлять управление с прогнозированием и предупреждением возможных срывов в ходе работ;

- повышать эффективность управления операциями в экономике.

Определения и элементы сетевой модели.

1. Сетевым графиком называют графическое представление технологической последовательности ведения работ.

2. Сетевым графиком называют ориентированную транспортную сеть с одним входом (вершина, которая не имеет входящих дуг) и одним выходом (вершина, которая не имеет выходящих дуг).

Дуги сетевого графика интерпретируют работы. Вершины графика, соединённые дугами, называют событиями. Одна и та же вершина-событие может служить началом одних и концом других работ. Событие выражает факт окончания всех работ, входящих в него.

Если речь идёт о планировании во времени, то основным параметром является продолжительность выполнения операций. Если планирование – по ресурсам, то основной характеристикой является интенсивность потребления ресурса в единицу времени.

Работы сетевого графика могут быть действительными, т.е. имеющими продолжительность. Они изображаются сплошной линией со стрелкой на конце. Также, работы могут быть фиктивными. Фиктивные работы имеют нулевую продолжительность и служат для указания порядка следования работ. Изображаются такие работы пунктирной линией со стрелкой на конце.

В большинстве реальных проектов точное значение продолжительности работ t_ij неизвестно, но на основании опыта (экспертных оценок) могут быть предложены нижняя (оптимистическая) оценка a_ij, определяющая продолжительность работы в идеальных условиях и верхняя (пессимистическая) оценка b_ij, определяющая максимальную оценку продолжительности с учетом всех возможных срывов. При наличии некоторого опыта может быть определено наиболее вероятное время выполнения работы m_ij.

При реализации проекта составляется график выполнения ра­бот. Для того чтобы проект был завершен вовремя, необходимо контролировать сроки выполнения этих работ. Усложняющим фактором является то, что работы взаимосвязаны. Одни работы зависят от выполнения других и не могут начаться, пока предшест­вующие работы не будут завершены.

Важной предпосылкой применения метода СРМ является пред­положение о том, что время выполнения каждой работы точно известно.

В результате использования метода СРМ удается получить от­веты на следующие вопросы:

1. За какое минимальное время можно выполнить проект?

2. В какое время должны начаться и закончиться отдельные работы?

3. Какие работы являются «критическими» и должны быть вы­полнены точно в установленное время, чтобы не был сорван срок выполнения проекта?

4. На какое время можно отложить срок выполнения «некри­тической» работы, чтобы она не повлияла на срок выполне­ния проекта в целом?

Исходным шагом для применения метода СРМ является опи­сание проекта в виде перечня выполняемых работ с указанием их взаимосвязи. Для описания проекта используются два основных способа: табличный и графический.

Рассмотрим следующую таблицу, описывающую проект:

 

 

В первом столбце указаны наименования всех работ проекта. Их четыре: А, В, С, D. Во втором столбце указаны работы, непо­средственно предшествующие данной. У работ А и В нет предшест­вующих. Работе С непосредственно предшествует работа В. Это означает, что работа С может быть начата только после того, как завершится работа В. Работе D непосредственно предшествуют две работы: А и С. Это означает, что работа D может быть начата толь­ко после того, как завершатся работы А и С. В третьем столбце таблицы для каждой работы указано время ее выполнения. На основе этой таблицы может быть построено графическое описа­ние проекта:

 

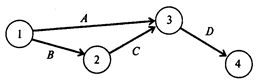
На рисунке проект представлен в виде графа с вершинами 1,2, 3, 4 и дугами А, В, С, D. Каждая вершина графа отображает собы­тие. Событие 1 означает начало выполнения проекта. Иногда та­кое событие обозначают буквой s ( start). Событие 4 означает за­вершение проекта. Для обозначения такого события иногда ис­пользуют букву f( finish). Любая работа проекта — это упорядочен­ная пара двух событии. Например, работа А есть упорядоченная пара событий (1, 3). Работа D — упорядоченная пара событий (3,4). Событие проекта состоит в том, что завершены все работы, «входящие» в соответствующую вершину. Например, со­бытие 3 состоит в том, что завершены работы А и С.

Рассмотрим другой проект, представленный следующей табли­цей:

 

 

Графическое описание проекта, построенное по этой таблице, имеет вид:

 

В этом графическом описании проекта, кроме тех работ, ко­торые указаны в таблице, использованы две «фиктивные» работы (3, 4) и (5, 6). На рисунке они показаны штриховыми линиями. Эти работы не требуют времени на их выполнение и используют­ся в графическом представлении проекта лишь для того, чтобы правильно отобразить взаимосвязь между работами. Получив гра­фическое представление проекта, мы обеспечили себе возмож­ность провести расчеты методом СРМ.

Определения:

Путь — последовательность взаимосвязанных работ, ведущая из одной вершины проекта в другую вершину. Например, {A, D, G} и {В, С, Е, С} — два различных пути, ведущие из вершины 1 в вер­шину 7.

Длина пути — суммарная продолжительность выполнения всех работ пути.

Критический путь — путь, суммарная продолжительность вы­полнения всех работ которого является наибольшей.

Ясно, что минимальное время, необходимое для выполнения любого проекта, равно длине критического пути. Именно на ра­боты, принадлежащие критическому пути, следует обращать осо­бое внимание. Если такая работа будет отложена на некоторое время, то и срок окончания проекта будет отложен на то же вре­мя. Если необходимо сократить время выполнения проекта, то в первую очередь нужно сократить время выполнения хотя бы од­ной работы на критическом пути.

Для того чтобы найти критический путь, достаточно перебрать все пути и выбрать тот или те из них, что имеют наибольшую сум­марную продолжительность выполнения работ. Однако для боль­ших проектов реализация такого подхода связана с вычислитель­ными трудностями. Метод СРМ позволяет получить критический путь намного проще.

Пусть i и j — вершины, или события, проекта, (i , j) — работа проекта, s — событие «начало проекта» (start), f — событие «окон­чание проекта» (finish), Т — длина критического пути.

Введем следующие обозначения:

t( i , j) — время выполнения работы (i, j);

ES( i , j) —наиболее раннее время начала работы ( i , j);

EF( i , j) —наиболее раннее время окончания работы ( i , j);

LS( i , j) —наиболее позднее время начала работы ( i , j),

LF( i , j) — наиболее позднее время окончания работы ( i , j),

E_i — наиболее раннее время наступления события i;

L_i — наиболее позднее время наступления события i;

R( i , j) — полный резерв времени на выполнение работы ( i , j) (время, на которое может быть отложена работа ( i , j) без увеличения продолжительности выполнения все­го проекта);

r( i , j) — свободный резерв времени на выполнение работы ( i , j) (время, на которое может быть отложена работа ( i , j) без увеличения наиболее раннего времени Е _i наступ­ления последующего события j ).

Если ( i , j) — работа проекта, то имеют место соотношения:

для любого j ES( i , j) = Е _i ;

для любого i LF( i , j) = L_j.

Для того чтобы использовать метод СРМ для нахождения критического пути, необходимо для каждой работы ( i , j) опреде­лить наиболее раннее время начала и окончания работы (ES(i,j) и EF( i , j)) и наиболее позднее время начала и окончания работы (LS( i , j) и LF( i , j)).

Метод СРМ описывается следующими соотношениями:

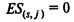
для любой работы ( s, j), выходящей из стартовой вершины s про­екта;

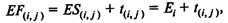
т.е. наиболее раннее время окончания любой работы ( i , j) превы­шает наиболее раннее время начала этой работы (время наступ­ления предшествующего события i ) на время ее выполнения;

т.е. наиболее раннее время начала работы ( q, j) равно наиболь­шему из значений наиболее раннего времени окончания непо­средственно предшествующих ей работ;

т.е. длина критического пути равна наиболее раннему времени завершения проекта;

т.е. наиболее позднее время окончания любой работы, заверша­ющей проект, равно длине критического пути;

т.е. наиболее позднее время начала любой работы меньше наибо­лее позднего времени окончания этой работы (времени наступле­ния последующего события) на время ее выполнения;

т.е. наиболее позднее время окончания работы (/, q) равно наи­меньшему из значений наиболее позднего времени начала непо­средственно следующих за ней работ;

т.е. полный резерв времени на выполнение любой работы равен разности между наиболее поздним и наиболее ранним временем ее начала или разности между наиболее поздним и наиболее ран­ним временем ее окончания;

т.е. свободный резерв времени на выполнение любой работы ра­вен разности между наиболее поздним временем наступления последующего события и наиболее ранним временем окончания работы.

Из приведенных выше определений и соотношений непосред­ственно вытекают следующие утверждения:

1. Длина критического пути равна Т.

2. Если R( i , j) = 0, то работа ( i , j) лежит на критическом пути;

если R(i,j) > 0, то работа ( i , j) не лежит на критическом пути.

3. Если время начала работы ( i , j), не лежащей на критичес­ком пути, отложить на срок меньший, чем r( i , j), то наиболее ран­нее время наступления последующего события не изменится.

4. Если время начала работы ( i , j), не лежащей на критичес­ком пути, отложить на срок меньший, чем R(i,j), то время, необ­ходимое на выполнение всего проекта, не увеличится.

 

ЗАДАЧА

Холдинговая компания планирует распределить среди предприятий холдинга начальную сумму средств e⁰ = 40 млн. руб., причем средства выделяются кратно, по 10 млн. руб., и распределяются между тремя предприятиями П₁, П₂, П₃.

Предоставление предприятию П_k средств u^k приносит доход f_k (u^k), который задан в исходной таблице. Определить, какое количество средств нужно предоставить каждому предприятию, чтобы обеспечить холдингу максимальный суммарный доход.

 

x	0	10	20	30	40
f1(x)	0	4	5	7	8
f2(x)	0	3	3	4	6
f3(x)	0	4	4	5	6

 

Решение задачи проводим поэтапно.

I этап. Осуществим условную оптимизацию распределения денежных средств.

При этом столбцы 1, 2 и 3 для всех трех таблиц одинаковы, поэтому их можно сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице третьего шага столбцы 5 и 6 отсутствуют).

Первый шаг. Положим, что k = 3.

e2	u3	e3 = e2 - u3	f3(u3)	F*3(e3)	u3(e3)
10	0	10	0	4	10
	10	0	4
20	0	20	0	4	10
	10	10	4
	20	0	4
30	0	30	0	5	30
	10	20	4
	20	10	4
	30	0	5
40	0	40	0	6	40
	10	30	4
	20	20	4
	30	10	5
	40	0	6

 

Второй шаг. Примем k = 2.

 

e1	u2	e2 = e1 - u2	f2(u2)	F*2(e1)	F1(u2,e1)	F*2(e2)	u2(e2)
10	0	10	0	4	4	4	0
	10	0	3	0	3
20	0	20	0	4	4	7	10
	10	10	3	4	7
	20	0	3	0	3
30	0	30	0	5	5	7	10
	10	20	3	4	7
	20	10	3	4	7
	30	0	4	0	4
40	0	40	0	6	6	8	10
	10	30	3	5	8
	20	20	3	4	7
	30	10	4	4	8
	40	0	6	0	6

 

Третий шаг. Считаем, что k = 1.

 

e0	u1	e1 = e0 - u1	f1(u1)	F*1(e0)	F0(u1,e0)	F*1(e1)	u1(e1)
10	0	10	0	4	4	4	0
	10	0	4	0	4
20	0	20	0	7	7	8	10
	10	10	4	4	8
	20	0	5	0	5
30	0	30	0	7	7	11	10
	10	20	4	7	11
	20	10	5	4	9
	30	0	7	0	7
40	0	40	0	8	8	12	20
	10	30	4	7	11
	20	20	5	7	12
	30	10	7	4	11
	40	0	8	0	8

 

В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.

 

Этап II. Проведем безусловную оптимизацию.

Из таблицы первого шага получим F*₃(e⁰ = 40) = 12. То есть максимальный доход всей системы при сумме средств e⁰ = 40 млн. руб. равен 12 млн. руб.
Из этой же таблицы получаем, что первому предприятию следует предоставить:

u*₁(e⁰ = 40) = 20 (млн. руб.).
При этом остаток средств составит:
e¹ = e⁰ – u¹
e¹ = 40 – 20 = 20 (млн. руб.).

 

Из таблицы второго шага имеем F*₂(e¹ = 20) = 7. Это означает, что максимальный доход всей системы при сумме предоставляемых средств e¹ = 20 млн. руб. равен 7 млн. руб.
Из этой же таблицы получаем, что второму предприятию следует направить:

u*₂(e¹ = 20) = 10 (млн. руб.).
При этом остаток средств составит:
e² = e¹ – u²
e² = 20 – 10 = 10 (млн. руб.).
Последнему предприятию остается 10 млн. руб.

Ответ:
Следовательно, максимальный доход холдинговой компанией будет получен в том случае, если:
- Первому предприятию предоставить 20 млн. руб.
- Второму предприятию выделить 10 млн. руб.
- Третьему предприятию направить 10 млн. руб.
При этом холдингом от этих трех предприятий будет получен максимальный доход, равный     12 млн. руб. (двенадцать миллионов руб. 00 коп.).