Нелинейное программирование

Источники не­линейности относятся в основном к одной из двух категорий:

1) Реально существующие и эмпирически наблюдаемые нели­нейные соотношения, например: непропорциональные зависимо­сти между объемом производства и затратами; между количеством используемого в производстве компонента и некоторыми показа­телями качества готовой продукции; между затратами сырья и физическими параметрами (давление, температура и т.п.) соответ­ствующего производственного процесса; между выручкой и объ­емом реализации и др.;

2) Установленные руководством правила поведения или задаваемые зависимости, например: формулы или правила расчета с потребителями энергии или других видов услуг; эвристические правила определения страховых уровней за­паса продукции; гипотезы о характере вероятностного распреде­ления рассматриваемых в модели случайных величин; различного рода договорные условия взаимодействия между партнерами по бизнесу и др.

Решать линейные задачи значительно проще, чем нелинейные, и если линейная модель обеспечивает адекватность реальным си­туациям, то ее и следует использовать. В практике экономичес­кого управления модели линейного программирования успешно применялись даже в условиях нелинейности. В одних случаях нелинейность несущественна и ею можно пренебречь, в других — производилась линеаризация нелинейных соотноше­ний или применялись специальные приемы, например, строились линейные аппроксимационные модели, благода­ря чему достигалась требуемая адекватность. Тем не менее, име­ется большое число ситуаций, где нелинейность является сущест­венной и ее нужно учитывать в явном виде. В общем виде задача НЛП описывается с помощью следующей моделинелинейного программирования:

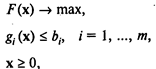
где х = (x₁, х₂, ..., х _n) — вектор переменных задачи.

Задача (1)—(3) называется задачей нелинейного программирова­ния в стандартной форме на максимум. Может быть сформулирована также задача НЛП на минимум.

Вектор х = (x₁, х₂, ..., х _n), компоненты х _j которого удовлетво­ряют ограничениям (2) и (3), называется допустимым решением или допустимым планом задачиНЛП. Совокупность всех допустимых планов называется множеством допустимых планов.Допустимое решение задачи НЛП, на котором целевая функ­ция (1) достигает максимального значения, называется оптималь­ным решением задачи НЛП.

Возможное местонахождение максимального значения функ­ции F(x) при наличии ограничений (2) и (3) определяется следующим общим принципом. Максимальное значение F(x), если оно существует, может достигаться в одной или более точках, кото­рые могут принадлежать следующим множествам:

 — внутренняя точка множества допус­тимых планов, в которой все первые частные производные

 — точка границы множества допус­тимых планов};

 — точка множества допустимых планов, в которой функция F(x) не дифференцируема}.

В отличие от задач линейного программирования, любая из ко­торых может быть решена симплекс-методом, не существует одного или нескольких алгоритмов, эффективных для решения любых нелинейных задач. Какой-то алгоритм может оказаться чрезвычай­но эффективным для решения задач одного типа и неудачным для задач другого типа. Эффективность алгоритма может даже существенно зависеть от постановки задачи, например от изменения масштабов тех или иных переменных. Поэтому алгоритмы разрабатываются для каждого класса (типа) задач. Программы, ориентированные на решение определенного класса задач, как правило, не гаран­тируют правильность решения любых задач данного класса, и оптимальность решения рекомендуется проверять в каждом кон­кретном случае.