Имитационное моделирование

Имитация — это попытка дублировать особенности, внешний вид и характеристики реальной системы. Идея имитации реали­зуется следующим образом: 1) математическое описание реальной ситуации; 2) изучение ее свойств и особенностей; 3) формирование выводов и принятие решений, связанных с воздействием на эту ситуацию и основанных на результатах имитации. Важно, что реальная система не подвергается воздействию до тех пор, пока преимущества или недостатки тех или иных управ­ленческих решений не будут оценены с помощью модели этой системы.

Метод Монте-Карло (метод статистических испытаний) состо­ит из четырех этапов:

1. Построение математической модели системы, описывающей зависимость моделируемых характеристик от значений стохасти­ческих переменных.

2. Установление распределения вероятностей для стохастичес­ких переменных.

3. Установление интервала случайных чисел для каждой сто­хастической переменной и генерация случайных чисел.

4. Имитация поведения системы путем проведения многих ис­пытаний и получение оценки моделируемой характеристики си­стемы при фиксированных значениях параметров управления. Оценка точности результата.

Широкое распространение получили два метода статистичес­ких испытаний. Один из них предполагает проведение достаточ­но большого числа Т последовательных наблюдений в течение одного прогона модели (одного сеанса имитирования). Второй метод заключается в реализации т независимых про­гонов модели, т.е. в m-кратном повторении одного и того же цикла имитирования. При этом, если мы хотим получить в сумме Т наблюдений, в течение каждого прогона можно делать по Т/т (допустим, что это число целое) наблюдений. Оба метода дают примерно одинаковый результат.

Пусть значения у _t (t = 1,..., Т) представляют собой результа­ты Т последовательных измерений значений случайной величи­ны y во время одного и того же сеанса имитации. Среднее по вре­мени значение у определяется выражением

Обозначим через m математическое ожидание случайной вели­чины у. Тогда для достаточно большого T получаем

Оценка дисперсии 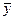 (если временной ряд не является авто-коррелированным) имеет вид

где D(у) — дисперсия случайной величины у.

Для оценки качества результатов, полученных методом Мон­те-Карло при неизвестной дисперсии наблюдаемой случайной величины, применяется Z — характеристика, которая долж­на быть определена (вероятность события, математическое ожи­дание, дисперсия и т.п.), a x — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограни­ченности числа T проведенных наблюдений. В этих условиях мож­но говорить о вероятности p(|Z – x| < e) по отношению к инте­ресующей нас характеристике. Величина |Z – e| представляет со­бой погрешность в оценке Z, a e — некоторый допустимый ее предел.

Из неравенства Чебышёва следует

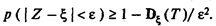
  Из этого неравенства следует

откуда при заданных р и e и при известной зависимости D_e (Т)можно найти предельно необходимое Т. Известно, что истинная дисперсия выборочного распределения для расчетного среднего обратно пропорциональна суммарному числу наблюдений Т, т.е.

где d не зависит от Т.

В начале имитационного процесса требуемое число наблюде­ний определить обычно не удается, поскольку d неизвестно. По­этому, как правило, эксперимент проводят в два этапа.

На первом этапе число испытаний выбирается относительно небольшим, в результате определяется величина d. После этого можно уже определить, сколько дополнительных наблюдений необходимо, чтобы была достигнута требуемая точность.

Предельное число наблюдений Т₀ определяется формулой T₀ = d/[(1 – p) e²].

При любом числе наблюдений больше Т₀ обеспечивается тре­буемая точность.