 |
Главная |
Связанных случайных процессов
|
из
5.00
|
Пусть X(t) и Y(t) – стационарные и стационарно связанные случайные процессы с 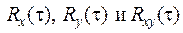 .
.
Рассмотрим X(t), Y(t) на 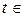 [–T, T],
[–T, T], 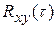 ,
, 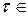 [–2T, 2T].
[–2T, 2T].
Запишем 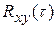 через преобразование Фурье с периодом 4 T
через преобразование Фурье с периодом 4 T
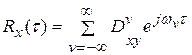 , (13)
, (13)
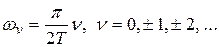
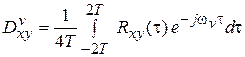 . (14)
. (14)
Для рассмотрения при Т → ∞ введем функцию
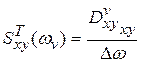 , (15)
, (15)
Dw = 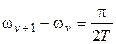 .
.
Тогда
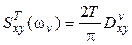 . .
| (16) |
Подставляя (16) в (13) →
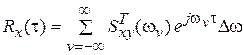
| (17) |
Для (16) 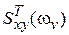 с учетом (14) с учетом (14)
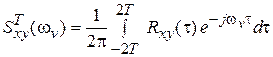
| (18) |
При Т → ∞
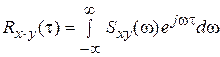 ; ;
| (19) |
Взаимная спектральная плотность X(t) и Y(t), между ними преобразование Фурье. Для X(t) – вектор: 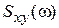 – n n – матрица спектральной плотности: – n n – матрица спектральной плотности:
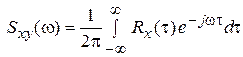 . .
| (20) |
Если X(t) – вектор, то 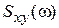 – n х n – матрица спектральной плотности: – n х n – матрица спектральной плотности: 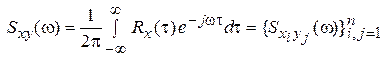 . .
| (21) |
Белый шум – стационарный случайный процесс с постоянной спектральной плотностью.
Пусть белый шум V(t).
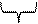
Корреляционная функция белого шума:
Поскольку 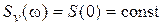 , то по формуле (8)
, то по формуле (8) 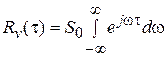 .
.
 Пусть
Пусть 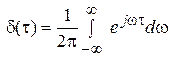 – импульсная функция.
– импульсная функция.
голоморфная функция на замкнутом контуре
(в ряд Тейлора)
Тогда
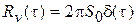
| (22) |
На основании свойств 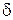 -функции из (22) получим -функции из (22) получим
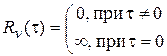
| (23) |
Это означает, что сечения случайного процесса типа белого шума являются некоррелированными случайными величинами с бесконечными дисперсиями
. 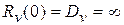
| (24) |
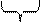 Это удобная математическая абстракция. В некотором диапазоне частот белый шум реально есть.
Это удобная математическая абстракция. В некотором диапазоне частот белый шум реально есть.
Рассмотрим случайный процесс V(t) с математическим ожиданием
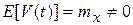 и
и 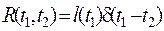 ,
, 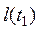 – обычная функция.
– обычная функция.
Такой процесс сохраняет свойство некоррелированности различных сечений ( 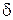 – некоррелированности). Однако он представляет собой нестационарный случайный процесс, поэтому процесс V(t) – нестационарный белый шум и
– некоррелированности). Однако он представляет собой нестационарный случайный процесс, поэтому процесс V(t) – нестационарный белый шум и 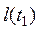 – интенсивность.
– интенсивность.
Можно представить белый шум в виде вектора
V (t)=[ V1, V 2, … Vn ]Т .
Тогда 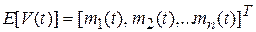 .
.
Корреляционная матрица
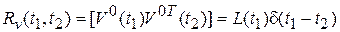 , где
, где 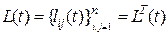 – матрица интенсивностей.
– матрица интенсивностей.
ПРАВИЛА ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ЛИНЕЙНЫМ ОПЕРАТОРОМ
Рассмотрим пример одновходной одновыходной одномерной системы.
Пусть X(t) – входной сигнал с 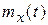 и
и 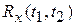 .
.
Требуется найти 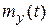 и
и 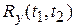 выходного сигнала Y(t).
выходного сигнала Y(t).
система управления
 Таким образом: X(t) Y(t). Это означает, что каждой реализации x(t) сопоставляется y(t) посредством действия на x(t) оператором системы обозначим его А.
Таким образом: X(t) Y(t). Это означает, что каждой реализации x(t) сопоставляется y(t) посредством действия на x(t) оператором системы обозначим его А.
Тогда Y(t) = А t [X(t)].
С учетом коммутативности линейных операторов E и А t
С учетом коммутативности линейных операторов E и А t
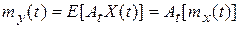
| (1) |
| Корреляционная функция выходного сигнала | |
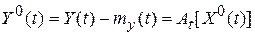
| (2) |
Тогда
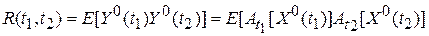
| (3) |
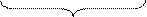 По коммутативности E и А t → По коммутативности E и А t →
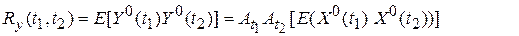
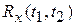
| |
Окончательно 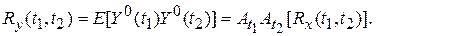
| (4) |
Многомерный случай (Многовходная многовыходная многомерная система)
Пусть X(t) – n-вектор, Y(t) – m-вектор, 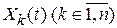 преобразуется в
преобразуется в 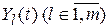 соответствующим оператором, т.е.
соответствующим оператором, т.е. 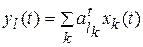 ,
, 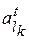 –
–
Коэффициент. Или
| Y(t) = А t [X(t)], | (5) |
где А t – m n матрица операторов.
Задача преобразования входных случайных сигналов многомерной системой. Даны статистические характеристики входных сигналов:
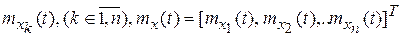 ;
;
корреляционная функция
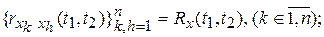
Матрица операторов 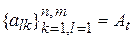 .
.
Требуется найти статистические характеристики входных сигналов:
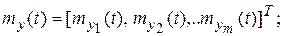
корреляционную функцию Y(t) определяется с учетом коммутативности операторов
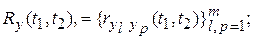
взаимные корреляции функций
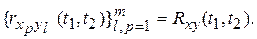
Формула для математического ожидания E и А:
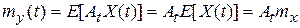 .
.
Формула для корреляционной функции 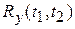
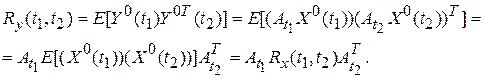
Формула для взаимнокорреляционной функции 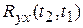
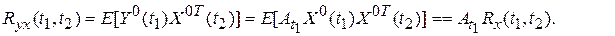 Аналогично:
Аналогично: 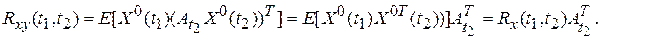
Статистические характеристики выходных сигналов
Элементарных звеньев
Математическое ожидание и корреляционная функция выходного
сигнала суммирующего звена
Пусть на вход суммирующего устройства поступает n случайных сигналов 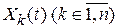 с
с 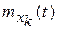 и
и 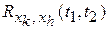 ,
, 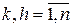 .
.
Суммирующее звено осуществляет операцию суммирования входных сигналов и оператор для каждого сигнала равен 1.
Тогда 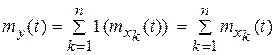 ,
,
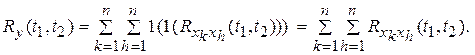
В частности, когда входные сигналы являются некоррелируемыми случайными процессами имеет место: 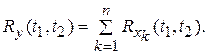
Математическое ожидание и корреляционная функция выходного сигнала дифференцирующего звена
Здесь 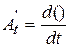 , ,
| (*) |
так как 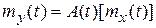 , то для (*)
, то для (*) 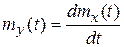 ,
,
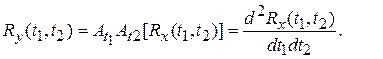
Это можно обобщить и на n производных.
Заметим, что обычное понятие производной для случайной функции X(t) не применимо.
Производная случайной функции X(t) есть предел отношения приращения функции к приращению аргумента в среднем квадратическом смысле:
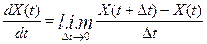 .
.
Предел в среднем квадратическом (сокращенно) означает, что 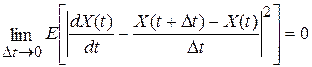 .
.
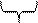 в обычном смысле
в обычном смысле
Существование 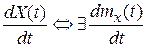 и
и 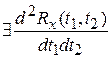 .
.
Пример.
Пусть X(t): 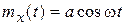 и
и 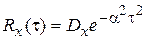 . Найти
. Найти 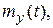
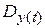 .
.
Решение.
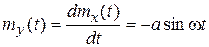 ,
, 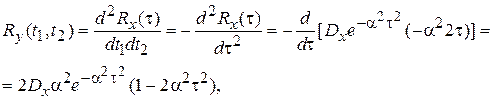
где 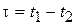 . При
. При 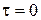 ,
, 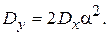
Лекция 3
Математическое ожидание и корреляционная функция выходного сигнала интегрирующего звена
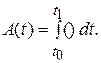
Тогда 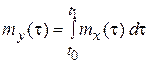 ,
, 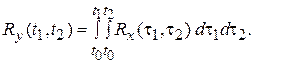
Пример. 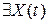 – белый шум.
– белый шум.
Тогда 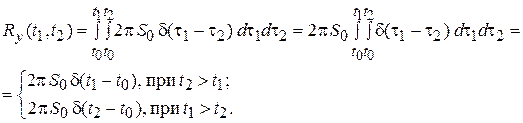
 |
уже другой случайный процесс.
Математическое ожидание и корреляционная функция выходного сигнала усилительного звена 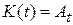
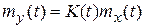 ;
; 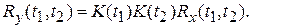
|
из
5.00
|
Обсуждение в статье: Связанных случайных процессов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

