 |
Главная |
МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ
|
из
5.00
|
(Марков Андрей Андреевич старший, 1856–1922 г.г.)
В зависимости от непрерывного или дискретного tÎ[0, T] и случайной величины x (t) различают 4 основных вида Марковских случайных процессов:
1. Марковские цепи (дискретный случайный процесс с дискретным временем).
2. Дискретный Марковский процесс (дискретный случайный процесс с непрерывным временем).
3. Марковские последовательности (непрерывный случайный процесс с дискретным временем).
4. Непрерывнозначный Марковский процесс (непрерывный случайный процесс с непрерывным временем).
Определение. Случайный процесс x (t) называется Марковский, если для любых n моментов времени t1< t2<…<tn из отрезка Î[0, T] условная функция распределения «последнего» значения x (tn) при фиксированных x(t1), xt2) ,…, x (tn -1) зависит только от x (tn -1), т.е. при заданных значениях x1, x2 ,…, xn -1 справедливо соотношение
P{x (tn) £ xn | x (t1) = x1, x(t2) = x2 ,…, x( tn -1) = xn -1 }=
= P {x (tn) £ xn|x (tn -1) = xn -1}. (1)
Для трех моментов времени tk < tj <ti (1) принимает вид
P {x (ti) £ xi | x (tk) = xk, x( tj) = xj }=
= P {x (ti) £ xi |x( tj) = xj}. (2)
Таким образом, если точно известно состояние Марковского процесса (МП) в момент времени tj , будущее (при ti) и прошлое (при tk) состояния МП независимы.
Другое определение. Для tk < tj <ti
{x (ti) £ xi, x (tk) £ xk | x( tj) = xj}=
= P {x (ti) £ xi | x( tj) = xj}× P {x (tk) £ xk | x( tj) = xj}, (3)
Это определение симметричное относительно времени и означает, что при фиксированном состоянии случайного процесса в настоящий момент времени tj будущее (при ti) и прошлое (при tk) состояния Марковского процесса независимы.
Другое важное свойство: эволюция вероятности перехода
P {x (t) £ x | x( t0) = x0}описывается уравнением вида dP/dt = AP, (4)
где А – некоторый линейный оператор (матрица, дифференциальный оператор и др.). Тогда можно использовать методы дифференциальных уравнений.
Пусть заданы начальные условия в начальный момент t0 . Тогда при отсутствии каких-либо ограничений нужно записать решение (4) и, при задании начальных условий, найти решение.
Если же имеются еще и ограничения (граничные условия), то нужно при нахождении решения использовать их.
Например, точка, отражающая поведение системы, начиная движение из начального состояния x( t0) = x0, при достижении границы x( t) = С «поглощается» ею и работа системы прекращается (нарушается) (траектория 1); точка «отражается от границы» (траектория 2) и т.д.

Если граница поглощающая, то помимо отыскания вероятности перехода Р для x < С, можно интересоваться вероятностью «поглощения» за некоторое Т или же математическим ожиданием, дисперсией и другими характеристиками времени Т, когда траектория впервые достигает границы С.
Задачи указанного характера имеют математически строгое решение только для Марковского процесса.
1. Простая цепь Маркова. Пусть случайный процесс  принимает конечное число K различных дискретных значений v1, v2, …, vk в некоторые моменты t0 <t1 < t2 …< tN. Эти значения могут мгновенно изменяться, т.е. имеют место переходы vi ® vj i, j =
принимает конечное число K различных дискретных значений v1, v2, …, vk в некоторые моменты t0 <t1 < t2 …< tN. Эти значения могут мгновенно изменяться, т.е. имеют место переходы vi ® vj i, j =  .
.
Характерное свойство простой цепи Маркова состоит в том, что
ver Р  значения процесса
значения процесса  в момент tn зависит лишь от того , какое значение имел процесс в непосредственно предшествующий ему момент времени tn –1 и не зависит от значений процесса в более ранние моменты времени, т.е
в момент tn зависит лишь от того , какое значение имел процесс в непосредственно предшествующий ему момент времени tn –1 и не зависит от значений процесса в более ранние моменты времени, т.е  .
.
Поэтому для простой цепи Маркова совместные конечномерные цепи Маркова вычисляются как:
 . (5)
. (5)
Условные вероятности 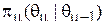 принято называть вероятностями перехода из состояния
принято называть вероятностями перехода из состояния  в состояние
в состояние  за промежуток времени
за промежуток времени  .
.
Одна из основных задач в теории простых цепей Маркова:
Пусть задано начальное значение случайного процесса при  и указан вероятностный закон смены соседних значений СП (т.е. заданы ver перехода).
и указан вероятностный закон смены соседних значений СП (т.е. заданы ver перехода).
Каким образом можно найти вероятности различных значений СП в момент времени  и, в частности, при
и, в частности, при  ?
?
Введем обозначения для безусловных и условных вероятностей:  (6)
(6)
Величина  есть безусловная вероятность значения
есть безусловная вероятность значения 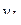 на n-м шаге (при
на n-м шаге (при  ), а
), а 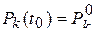 начальное вероятностное значение
начальное вероятностное значение  .
.
Условная вероятность  определяет вероятность значения
определяет вероятность значения  при
при 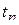 , если в более ранний момент времени
, если в более ранний момент времени  значение СП было равно
значение СП было равно  .
.
Эти вероятности неотрицательны и удовлетворяют условию нормировки:
 (7)
(7)
 (8)
(8)
На основании правила полной вероятности получаются уравнения Маркова:
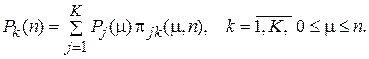 (9)
(9)
Выполняется:
 (10)
(10)
Среди простых цепей Маркова выделяются однородные цепи, где вероятности перехода  зависят лишь от разности аргументов, т.е.
зависят лишь от разности аргументов, т.е.
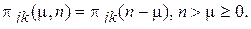 (11)
(11)
Обозначим одношаговые вероятности перехода через  .
.
Полное вероятностное описание простой однородной цепи Маркова достигается заданием начальных вероятностей 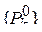 и матрицы одношаговых вероятностей перехода
и матрицы одношаговых вероятностей перехода
 . (12)
. (12)
Таким образом, для простой однородной цепи Маркова матрица вероятностей перехода за n шагов равна
 (13)
(13)
а матрица вероятностей различных значений СП:
 (14)
(14)
где  - матрица-строка безусловных вероятностей различных значений СП на
- матрица-строка безусловных вероятностей различных значений СП на  -м шаге;
-м шаге;  при шаге
при шаге  .
.
Однородная цепь Маркова, для которой вероятности  , т.е. не зависит от
, т.е. не зависит от  называется стационарной, в противном случае - нестационарной.
называется стационарной, в противном случае - нестационарной.
В общем случае  , если они существуют, находятся в результате предельного перехода
, если они существуют, находятся в результате предельного перехода
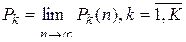 (15)
(15)
и называются финальными вероятностями.
Если  - стационарная цепь Маркова начинается с
- стационарная цепь Маркова начинается с  .
.
Финальные вероятности должны удовлетворять системе k линейных алгебраических уравнений
 (16)
(16)
и дополнительно условию
 (17)
(17)
Если взять  и, учитывая (8), т.е.
и, учитывая (8), т.е. 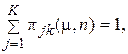 приходим к тождеству.
приходим к тождеству.
Поэтому k уравнений в (16) являются линейно зависимыми, и k финальных вероятностей следует определять из (k -1) уравнений (16) уравнения (17).
2. Дискретный марковский процесс.
Пусть  по-прежнему принимает только дискретные значения
по-прежнему принимает только дискретные значения
v1, v2, …, vk ,но смена этих значений происходит не в фиксированные, а в любые случайные моменты времени. Вероятности перехода
 (18)
(18)
Удовлетворяют следующим соотношениям
 , (19)
, (19)
 . (20)
. (20)
Кроме того, для них справедливо уравнение Колмогорова-Чэпмена:
 (21)
(21)
Характерное свойство: для малых  вероятность
вероятность  того, что значение не изменится, превышает вероятность изменения значения:
того, что значение не изменится, превышает вероятность изменения значения:
 (22)
(22)
так как вероятность перехода из одного значения в другое неотрицательны, т.е. 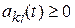 , и для них должно выполняться условие нормировки (19), то из (22) получаем
, и для них должно выполняться условие нормировки (19), то из (22) получаем
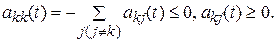 (23)
(23)
В (22)  .
.
Подставляя (22) в (21) и  получим систему линейных дифференциальных уравнений
получим систему линейных дифференциальных уравнений
 , (24)
, (24)
где  (t)удовлетворяет (23). Решение этой системы при начальных условиях (20)дает зависимость вероятностей перехода от времени.
(t)удовлетворяет (23). Решение этой системы при начальных условиях (20)дает зависимость вероятностей перехода от времени.
Замечания. Дискретный марковский процесс остается марковским и в обратном направлении, т.е. наряду с (24) (прямые дифференциальные уравнения) справедливы обратные уравнения
 . (25)
. (25)
Уравнениям (24) удовлетворяют не только вероятности перехода, но и безусловные вероятности значений 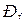 (t):
(t):
 (26)
(26)
Их нужно интегрировать при начальных условиях
 (t)=
(t)=  . (27)
. (27)
Дискретный марковский процесс называется однородным, если вероятности перехода 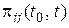 зависят только разности
зависят только разности 
 . (28)
. (28)
Если при  существует
существует  которые не зависят от начального состояния, то марковский процесс – стационарный марковский процесс, и вероятности стационарных значений определяются системой алгебраических уравнений:
которые не зависят от начального состояния, то марковский процесс – стационарный марковский процесс, и вероятности стационарных значений определяются системой алгебраических уравнений:
 (29)
(29)
3. Марковские последовательности(МП).
Пусть случайные величины  в некоторые дискретные моменты времени t1 < t2 …< tn …< tN принимают непрерывные множества возможных значений.
в некоторые дискретные моменты времени t1 < t2 …< tn …< tN принимают непрерывные множества возможных значений.
Определяющее свойство марковской последовательности  состоит в том, что совместная плотность вероятности рассматриваемых случайных величин выражается через плотность вероятности начального состояния
состоит в том, что совместная плотность вероятности рассматриваемых случайных величин выражается через плотность вероятности начального состояния  и плотности вероятности перехода
и плотности вероятности перехода  :
:
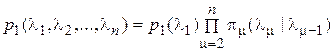 . (31)
. (31)
Основные свойства марковской последовательности:
1. Если точно известно значение МП в настоящий момент t, то ее будущее значение не зависит от предыдущего состояния.
2. Любая последовательность, взятая из марковской, является также марковской.
3. МП остается марковской и в обратном направлении.
4. Плотность вероятности перехода удовлетворяет уравнению
 (32)
(32)
МП называется однородной, если плотности ver перехода  не зависят от n .
не зависят от n .
МП называется стационарной, если она однородна и все случайные величины  имеют одну т ту же плотность вероятности:
имеют одну т ту же плотность вероятности:  .
.
4. Непрерывнозначный марковский процесс (НМП).
Область значений непрерывнозначного процесса 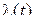 и область его определения [0, T] есть непрерывные множества. Для НМП диффузного типа плотность ver перехода
и область его определения [0, T] есть непрерывные множества. Для НМП диффузного типа плотность ver перехода  и безусловная плотность вероятности
и безусловная плотность вероятности 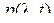 удовлетворяет уравнению в частных производных Фоккера-Планка-Колмогорова, которое применительно к плотности ver
удовлетворяет уравнению в частных производных Фоккера-Планка-Колмогорова, которое применительно к плотности ver  имеет вид:
имеет вид:
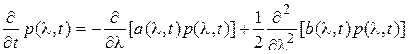 , (33)
, (33)
или иначе,
 (34)
(34)
где
 . (35)
. (35)
«Коэффициенты» сноса 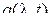 и диффузии
и диффузии  определяются по исходному стохастическому дифференциальному уравнению, описывающему поведение рассматриваемой системы, в виде:
определяются по исходному стохастическому дифференциальному уравнению, описывающему поведение рассматриваемой системы, в виде:
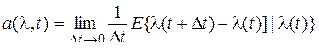 , (36)
, (36)
 . (37)
. (37)
Если стохастическое дифференциальное уравнение имеет вид
 , (38)
, (38)
где 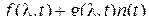 и – детерминированные формы своих аргументов, – (гауссовский) белый шум с нулевым математическим ожиданием и корреляционной функцией
и – детерминированные формы своих аргументов, – (гауссовский) белый шум с нулевым математическим ожиданием и корреляционной функцией
 , (39)
, (39)
то коэффициенты сноса и диффузии равны
 . (40)
. (40)
Коэффициент сноса 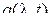 характеризует среднее значение локальной скорости МП , а коэффициент диффузии
характеризует среднее значение локальной скорости МП , а коэффициент диффузии  – локальную скорость изменения дисперсии (приращения). Если плотность ver перехода зависит лишь от разности временных аргументов
– локальную скорость изменения дисперсии (приращения). Если плотность ver перехода зависит лишь от разности временных аргументов 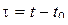 , а коэффициенты a и b не зависят от
, а коэффициенты a и b не зависят от  и
и  , то рассматриваемый процесс
, то рассматриваемый процесс  называется однородным во времени.
называется однородным во времени.
При начальных условиях  безусловная плотность вероятности
безусловная плотность вероятности 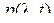 совпадает с плотностью вероятности перехода
совпадает с плотностью вероятности перехода  . При этом решение уравнения Фоккера-Планка-Колмогорова (ФПК) (33) называется фундаментальным решением.
. При этом решение уравнения Фоккера-Планка-Колмогорова (ФПК) (33) называется фундаментальным решением.
Для отыскания решения ФПК(33) необходимо задать начальное условие  (41)
(41)
и указать граничные условия.
Граничные условия могут быть весьма разнообразными и определяются существом физической задачи.
Приведем три вида:
1. Если случайный процесс  может принимать всевозможные значения от
может принимать всевозможные значения от  до
до  , то обычно выполняются нулевые граничные условия
, то обычно выполняются нулевые граничные условия
 . (42)
. (42)
2. Если случайный процесс  может принимать значения лишь в ограниченном интервале (c, d), причем в точках c, d помещены отражающие границы: траектория на них зеркально отражается. Тогда выполняются условия отражения границ:
может принимать значения лишь в ограниченном интервале (c, d), причем в точках c, d помещены отражающие границы: траектория на них зеркально отражается. Тогда выполняются условия отражения границ:
 .
.
3. В точках c, d расположены поглощающие границы: траектория на них поглощается и исключается из рассмотрения. Тогда должны выполняться условия поглощения:
 .
.
СТАТИСТИЧЕСКИЙ АНАЛИЗ И ОЦЕНКА ТОЧНОСТИ
НЕЛИНЕЙНЫХ СИСТЕМ
Некоторые замечания:
a) точных методов для решения нелинейных задачне разработано,
b) для некоторых частных задач найдены методы определения законов распределения, если процессы в исследуемой нелинейной системе –марковские.
В основе лежит использование дифференциальных уравнений в частных производных для плотностей вероятности. Однако этот путь приводит к сложным алгоритмам, реализуемым приближенно.
Наиболее универсальным приближенным методом является метод статистических испытаний (метод Монте-Карло). Однако нужно знать статистические характеристики входных сигналов, хотя не нужно знать вход-выходные соотношения.
Имеются приближенные методы. Среди них метод эквивалентных возмущений, в котором случайные входные сигналы разложены в степенной ряд по значениям случайных коэффициентов канонического разложения входных сигналов.
Метод позволяет находить моменты выходных случайных сигналов любого порядка, если известны соответствующие моменты случайных коэффициентов канонического разложения входных сигналов и случайных параметров системы.
- Наиболее простым приближенным методом является метод статистической линеаризации, причем для любых (но безынерционных) нелинейностей. Здесь нелинейная система состоит из нелинейного безынерционного блока и линейной инерционной части.
СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ БЕЗЫНЕРЦИОННЫХ
НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Метод статистической линеаризации означает замену нелинейного вход-выходного соотношения линейным относительно входного случайного сигнала.
Соответствующее линеаризованное звено называется эквивалентным относительно нелинейного звена.
Пусть дано нелинейное звено, для которого
 . (1)
. (1)
Для эквивалентного звена (1) заменяется приближенной зависимостью вида
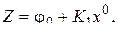 (2)
(2)
 - подлежат определению.
- подлежат определению.
Здесь  - статистическая средняя характеристика эквивалентного звена и выбирается так, чтобы
- статистическая средняя характеристика эквивалентного звена и выбирается так, чтобы
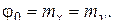 (3)
(3)
Для нелинейных звеньев с нечетными функциями  статистическую характеристику удобно представить в виде
статистическую характеристику удобно представить в виде  где
где  -статистический коэффициент усиления эквивалентного звена по средней составляющей (математического ожидания).
-статистический коэффициент усиления эквивалентного звена по средней составляющей (математического ожидания).
Таким образом,
 (4)
(4)
Характеристика  - статистический коэффициент усиления эквивалентного звена по случайным составляющим (флуктуациям).
- статистический коэффициент усиления эквивалентного звена по случайным составляющим (флуктуациям).
Коэффициент  выбирается двумя способами.
выбирается двумя способами.
Первый способ. Из условий равенства дисперсий:
 .
.
Знак определяется характером j(x): если j(x) возрастает вблизи точки
x = mx, то принимается K1> 0 и если убывает, то K1< 0 .
Второй способ. Значение  определяется из условия
определяется из условия
 (5)
(5)
Условие (5) перепишем в виде:
 (6)
(6)
 Условие минимума (6):
Условие минимума (6): 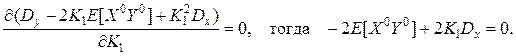

В результате 
Искомые величины  эквивалентного звена находят по приведенным формулам, если известны плотность вероятности
эквивалентного звена находят по приведенным формулам, если известны плотность вероятности  входного сигнала и характеристика
входного сигнала и характеристика  данного нелинейного звена.
данного нелинейного звена.
 Таким образом, Y
Таким образом, Y

Y






 X0 Y
X0 Y
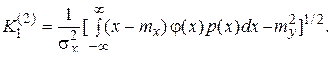
Для эквивалентного звена с нечеткой характеристикой эквивалентное звено можно представить, как усилительное звено с двумя каналами передави: один канал – для средней составляющей  ; другой – для случайной составляющей
; другой – для случайной составляющей  входного сигнала.
входного сигнала.

Однако коэффициенты 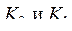 взаимосвязаны, так как у них общий случайный процесс X.
взаимосвязаны, так как у них общий случайный процесс X.
Плотность вероятности  входного сигнала нелинейного звена замкнутой системы неизвестна.
входного сигнала нелинейного звена замкнутой системы неизвестна.
Однако есть облегчающее предположение, поскольку система содержит линейную инерционную часть. Инерционная часть обладает свойством нормализации закона распределения входного сигнала. (Нужны первые два момента для определения случайного процесса).
Действительно,
 (*)
(*)
Как видно из (*) текущее значение Y(t), есть сумма от предыдущих значений со своими весами. Для инерционной системы эта сумма является суммой достаточно большого количества равномерно малых слагаемых, так как  для инерционных систем достаточно медленно убывают к нулю.
для инерционных систем достаточно медленно убывают к нулю.
Если бы эти значения были независимы, распределение выходного сигнала на основании центральной предельной теоремы было бы нормальным.
В действительности эти значения не независимы, однако «нормализация» в некотором смысле при их суммировании будет происходить. Чем более инерционная система, тем выше эффект «нормализации» системы.
Наиболее неблагоприятна ситуация, когда линейная часть системы малоинерционна и полоса пропускания совпадает (или несколько шире) с полосой спектра входного случайного сигнала.
Итак,  принимается в виде нормального закона и, следовательно, значения
принимается в виде нормального закона и, следовательно, значения  для такой нелинейности будут функциями
для такой нелинейности будут функциями  и
и  , т. е.
, т. е.


 (**)
(**)
Для типовых нелинейностей формулы (**) составлены.
Имеется связь между  и
и 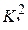 при нормальном законе распределения
при нормальном законе распределения
входного сигнала
 .
.
Используем выражение  и продифференцируем его по
и продифференцируем его по  . Тогда получим:
. Тогда получим:

ПРИМЕНЕНИЕ МЕТОДА СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА НЕЛИНЕЙНЫХ СИСТЕМ
Стационарная задача определения характеристик точности – математического ожидания  и
и  выходного сигнала характеризуется тем, что должны быть выполнены три условия: система стационарная; входные сигналы
выходного сигнала характеризуется тем, что должны быть выполнены три условия: система стационарная; входные сигналы  на входе всех нелинейных звеньев являются стационарными случайными процессами; система рассматривается в установившемся режиме. При этом статистические характеристики входных сигналов
на входе всех нелинейных звеньев являются стационарными случайными процессами; система рассматривается в установившемся режиме. При этом статистические характеристики входных сигналов  ,
,  ,
,  и коэффициенты
и коэффициенты 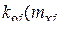 ,
, 
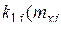 ,
,  являются постоянными величинами. Центрированное состояние выходного сигнала
являются постоянными величинами. Центрированное состояние выходного сигнала  также представляет собой стационарный случайный процесс.
также представляет собой стационарный случайный процесс.
Решение задачи определения характеристик точности системы с n нелинейными безынерционными звеньями состоит в следующем:
нелинейные звенья заменяются эквивалентными с соответствующими коэффициентами  ,
, 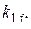 Таким образом, получается линеаризованная система с двумя каналами и двумя передаточными функциями по средней составляющей
Таким образом, получается линеаризованная система с двумя каналами и двумя передаточными функциями по средней составляющей  и по случайной составляющей
и по случайной составляющей  .
.
Используя формулы для  и D линейных стационарных систем, запишем уравнения математического ожидания и дисперсии всех входных сигналов
и D линейных стационарных систем, запишем уравнения математического ожидания и дисперсии всех входных сигналов 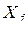 (
(  ) эквивалентных звеньев.
) эквивалентных звеньев.
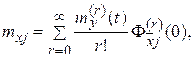 (1)
(1)
 (2)
(2)
где  - передаточная функция по средней составляющей;
- передаточная функция по средней составляющей;
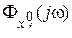 - частотная характеристика по случайной составляющей.
- частотная характеристика по случайной составляющей.
В (1) передаточные функции  содержат коэффициенты
содержат коэффициенты 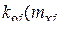 ,
,  а в (2) частотные характеристики
а в (2) частотные характеристики 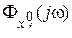 содержат коэффициенты
содержат коэффициенты 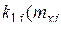 ,
,  . Каждый из коэффициентов
. Каждый из коэффициентов  ,
,  зависят от двух неизвестных
зависят от двух неизвестных 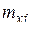 ,
,  . Поэтому совместное решение (1) и (2) дает значение
. Поэтому совместное решение (1) и (2) дает значение  ,
,  . Уравнения (1), (2) можно решить методом последовательных приближений. При этом первоначально задаются значения
. Уравнения (1), (2) можно решить методом последовательных приближений. При этом первоначально задаются значения  ,
,  и по формуле (1) и (2) вычисляются в первом приближении
и по формуле (1) и (2) вычисляются в первом приближении 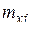 ,
,  . После этого уточняются значения
. После этого уточняются значения  ,
,  по формулам
по формулам
 ,
, 
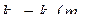 ,
, 
 ,
,  (*)
(*)
и вычисляются  ,
, 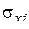 во втором приближении. Процесс продолжается до совпадения двух последних значений в пределах принятой точности.
во втором приближении. Процесс продолжается до совпадения двух последних значений в пределах принятой точности.
В частности, в одномерном случае (n = 1) (1) и (2) можно решать графически. Уравнение (1) приводится к виду
 . (3)
. (3)
Уравнение (2) приводится к виду:
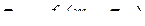 . (4)
. (4)
Совместное решение (3) и (4) означает, что
 . (5)
. (5)
 Задаваясь значениями
Задаваясь значениями 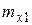 , построим в координатах два графика
, построим в координатах два графика  два графика
два графика  и
и  .
.
Вычисляя тем
| |
|
из
5.00
|
Обсуждение в статье: МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы
(0.013 сек.)

