 |
Главная |
Определение корреляционной функции и дисперсии через спектральную плотность входного сигнала
|
из
5.00
|
С учетом формулы 
получаем: 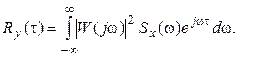
При  получаем:
получаем: 
Полученные результаты обобщаются на многомерный случай. Если ввести матрицу 
 , ,
|
 , ,
|
 , ,
|
 , ,
|
где  ,
,  – матрицы спектральных плотностей;
– матрицы спектральных плотностей;  ,
,  – матрицы взаимных спектральных плотностей.
– матрицы взаимных спектральных плотностей.
Лекция 4
Пример1. Рассмотрим статистические характеристики установившейся ошибки стационарной системы в частотном представлении.
Пусть на вход линейной стационарной системы поступает суммарный сигнал X(t) = Λ(t) + N(t), где
Λ(t) – полезный сигнал, стационарные и стационарно связанные случайные
N(t) – помеха, процессы с известными математическими
ожиданиями и спектральными плотностями.
Требуется найти статистические характеристики ошибки системы в стационарном режиме: математическое ожидание, спектральную плотность и дисперсию.
 Структурная схема
Структурная схема

Здесь число входов k =2, число выходов m = 1.
Математическое ожидание:  .
.
Передаточная функция ошибки по первому входу (по L(t)):
We1(p)= W(p) – W0(p).
Передаточная функция ошибки по первому входу (по N(t)): We2(p) = W(p).
mx1– математическое ожидание для L(t),
mx2– математическое ожидание для N(t).
| Спектральная плотность:
| |
Для некоррелированных сигналов L(t) и N(t):
 , ,
 – спектральная плотность полезного сигнала, – спектральная плотность полезного сигнала,
 – спектральная плотность помехи. – спектральная плотность помехи.
| (*) |
Дисперсия:
 .
Для случая некоррелированных входных сигналов L(t) и N(t): .
Для случая некоррелированных входных сигналов L(t) и N(t):
 . .
| (*) |
Отметим, что полученные соотношения для статистических характеристик ошибки системы справедливы тогда и только тогда, когда рассматривается устойчиваястационарная линейная система в установившемся режиме при стационарных и стационарно связанных входных случайных сигналах.
Замечание. Для определения дисперсии выходного сигнала системы вычисляются интегралы вида (*). Если спектральные плотности входных сигналов  представляют собой дробно-рациональные четные функции от w, вычисление интегралов (*) можно свести к вычислению интегралов стандартного типа. Значения этих интегралов получаются непосредственно через параметры спектральных плотностей входных сигналов и частотных характеристик.
представляют собой дробно-рациональные четные функции от w, вычисление интегралов (*) можно свести к вычислению интегралов стандартного типа. Значения этих интегралов получаются непосредственно через параметры спектральных плотностей входных сигналов и частотных характеристик.
Стандартный интеграл имеет вид:  ,
,
где An(w) = a0 wn + a1 wn –1+…+ an ;
Bn(w) = b0 w2n –2+ b1 w2n –4+…+ bn –1.
Значение этого интеграла определяется по формуле:  .
.
 – гурвицев определитель для полинома An(w). Определитель
– гурвицев определитель для полинома An(w). Определитель  формируется также как и
формируется также как и  , но с заменой первого столбца на b0 , b1 , … bn –1.
, но с заменой первого столбца на b0 , b1 , … bn –1.
 Пример 2. На вход линейной стационарной системы подается сигнал
Пример 2. На вход линейной стационарной системы подается сигнал
X(t) = Λ(t) + N(t).
Λ(t) – полезный случайный стационарный процесс со спектральной плотностью  .
.
Помеха N(t) – белый шум со спектральной плотностью S0 .
Найти дисперсию ошибки системы в установившемся режиме.

Решение
| |
 .
.
Дисперсию ошибки системы определим по формуле (*), считая для идеальной системы  ,
,




где 


 .
.
Общая формула:
 .
.
Здесь Dn – матрица Гурвица:
 ,
,  .
.
Тогда 
 .
.
 .
.
ФОРМИРУЮЩИЙ ФИЛЬТР. ЭКВИВАЛЕНТНАЯ СХЕМА
Формирующий фильтр –динамическая система, в которой при входном сигнале в виде белого шума N(t) имеет на выходе случайный сигнал X(t) с заданными статистическими характеристиками
При рассмотрении задачи формирования случайного сигнала X(t) достаточно сформировать только центрированный X(t), так как для формирования mx(t) достаточно прибавить некоторую неслучайную функцию.
Формирующий фильтр удобен в статистическом анализе систем управления с произвольными случайными входами, т.к. вместь входного сигнала ставится формирующий фильтр с белым шумом на входе. В результате получится эквивалентная система.
Формирующий фильтр (ФФ) используется также и при моделировании.
В общем случае задача построения ФФ не является простой. Например, когда данный случайный процесс X(t) имеет произвольную непрерывную корреляционную функцию, задача построения ФФ не решается. Решение имеется лишь для некоторого класса X(t). Однако, используя приближенные корреляционные функции или аппроксимации, этот класс существенно расширяется.
Задача решается точно, когда X(t) – стационарный процесс с дробно-рациональными спектральными плотностями.
Для определения линейного формирующего фильтра используется соотношение, устанавливающее связь между спектральными плотностями входного и выходного сигналов.
Пусть  – спектральная плотность на выходе ФФ.
– спектральная плотность на выходе ФФ.  – спектральная плотность на входе.
– спектральная плотность на входе.  – частотная характеристика ФФ.
– частотная характеристика ФФ.
Так как  , то
, то  .
.
Таким образом,  , (в которой все корни в левой полуплоскости).
, (в которой все корни в левой полуплоскости).
Пример3.  – спектральная плотность X(t) ,
– спектральная плотность X(t) ,  – спектральная плотность на входе.
– спектральная плотность на входе.
Тогда  .
.
Таким образом,  .
.
Аналогично для многомерного случая
 .
.
Выражение разрешимо, если  – дробно рациональные функции.
– дробно рациональные функции.
ОПРЕДЕЛЕНИЕ СТОХАСТИЧЕСКИХ ХАРАКТЕРИСТИК
ВЫХОДНЫХ СИГНАЛОВ МЕТОДАМИ МОДЕЛИРОВАНИЯ
Рассмотрим группы методов, когда выходные сигналы представляют собой стационарные случайные процессы.
Здесь выполняется тройка условий: стационарный случайный процесс; устойчивая стационарная система; устойчивый режим.
Рассмотри только определение  и
и  , так как вычисление математических ожиданий – тривиальная задача.
, так как вычисление математических ожиданий – тривиальная задача.
1) Модель процессов системы
 .
.
Введем новую переменную  .
.
Тогда  .
.
Так как  , то
, то
 .
.
Эту формулу можно переписать так:
 ,
,  ,
,
 .
.
Таким образом, получаем две одинаковые системы:
первая система: вход  – выход
– выход  ;
;
вторая система: вход 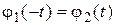 – выход
– выход  .
.

 . Здесь двухкратная модель системы.
. Здесь двухкратная модель системы.
2) Применение эквивалентной модели.
Рассматриваем последовательное соединение формирующего фильтра и данной линейной стационарной системы.
Обозначим через gэ (×) весовую функцию этого соединения, т.е. эквивалентной системы.
Тогда  .
.

Здесь  – корреляционная функция входного сигнала.
– корреляционная функция входного сигнала.
В результате  . Вводя новую переменную:
. Вводя новую переменную:  , получим
, получим  . Нижний предел можно расширить, т.к. по условию физической реализуемости
. Нижний предел можно расширить, т.к. по условию физической реализуемости  при t<
при t<  .
.
Имеет место следующий порядок в исследовании этой схемы:
– по спектральной плотности  входного сигнала X(t) определяется частотная характеристика формирующего фильтра (ФФ);
входного сигнала X(t) определяется частотная характеристика формирующего фильтра (ФФ);
– затем следует взять два одинаковых набора: ФФ + данная система;
– на вход одного набора подается d(t);
– на вход другого набора подается d(t–t);
– выходные сигналы перемножаются и интегрируются при t ® ¥ c умножением на  .
.
Таким образом, получается 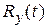 при t =
при t =  . Если
. Если  меняется, то производится многократное интегрирование.
меняется, то производится многократное интегрирование.
Дисперсия при  = 0:
= 0:  (Нужен один набор, но сквадратором.)
(Нужен один набор, но сквадратором.)
ОПРЕДЕЛЕНИЕ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК
НЕСТАЦИОНАРНЫХ СЛУЧАЙНЫХ СИГНАЛОВ
1) Модель процессов системы
– Математическое ожидание  (было).
(было).
Здесь на вход системы с 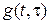 подается входной сигнал
подается входной сигнал  .
.
– Дисперсия 
Пусть  , тогда
, тогда
 .
.
Получается следующая процедура.
– На вход модели системы подается сигнал 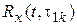 и формируется на выходе сигнал
и формируется на выходе сигнал  . Процедура повторяется n-раз при разных
. Процедура повторяется n-раз при разных  , k =
, k =  .
.
– По записи n кривых  определяется для заданного t =T функция
определяется для заданного t =T функция  (осреднение).
(осреднение).
– На вход модели системы подается сигнал в виде функции  и записывается выходной сигнал; значение выходного сигнала в момент
и записывается выходной сигнал; значение выходного сигнала в момент  =T равно дисперсии выходного сигнала для этого момента времени.
=T равно дисперсии выходного сигнала для этого момента времени.
Таким образом, для определения одного значения дисперсии выходного сигнала (при  =T) требуется n-кратное моделирование данной системы и получение промежуточной функции
=T) требуется n-кратное моделирование данной системы и получение промежуточной функции  .
.
МАТРИЦА КОВАРИАЦИЙ ВЕКТОРА СОСТОЯНИЯ
НЕСТАЦИОНАРНОЙ ЛИНЕЙНОЙ СИСТЕМЫ
Рассмотрим многомерную эквивалентную систему
 = F(t)Λ(t) + D(t)N (t), Λ(t0)= Λ0
= F(t)Λ(t) + D(t)N (t), Λ(t0)= Λ0
Y(t) = C(t)Λ(t) . (1)
Здесь Λ(t) – составной вектор (вектор системы + вектор ФФ). Начальное значение Λ(t0) задано математическим ожиданием  и корреляционной функцией
и корреляционной функцией  . N (t) – вектор белого шума с математическим ожиданием
. N (t) – вектор белого шума с математическим ожиданием  и матрицей интенсивностей L(t), причем N (t) некоррелирован с Λ(t0). Y(t) – исследуемый векторный выходной сигнал. F(t), D(t) , C(t) – заданные матрицы.
и матрицей интенсивностей L(t), причем N (t) некоррелирован с Λ(t0). Y(t) – исследуемый векторный выходной сигнал. F(t), D(t) , C(t) – заданные матрицы.
Ставится задача: определить матрицы ковариаций векторов Λ(t), Y(t) для 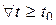 :
:
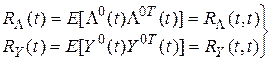 . (2)
. (2)
От общей задачи перейдем к задаче модифицированной для центрированного  , т.е.
, т.е.
 = F(t)Λ0(t) + D(t)N0 (t), Λ0 (t0) =
= F(t)Λ0(t) + D(t)N0 (t), Λ0 (t0) = 
Y0(t) = C(t)Λ0 (t) . (3)
Далее индекс «0» опускается.
Для решения поставленной задачи запишем производную искомой матрицы  .
.
 .
.
Рассмотрим слагаемое 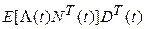 , а точнее ,
, а точнее ,  .
.
Таким образом,

Тогда,
 . (4)
. (4)
(4) – эквивалентно l2 скалярных уравнений, где l– размерность матрицы  .
.
В силу симметричности матрицы  г число их сокращается до
г число их сокращается до  .
.
С учетом соотношения Y(t) = C(t)L(t), получаем
 .
.
Пример 4. Система с выходом y(t) имеет модель I порядка:
 (*)
(*)
 - случайный процесс с корреляционной функцией
- случайный процесс с корреляционной функцией  .
.
Определить  выходного сигнала
выходного сигнала  .
.
Решение.
1. Выберем формирующий фильтр для стационарного центрированного сигнала  со спектральной плотностью
со спектральной плотностью  ,
,
 (соответствует во временной области
(соответствует во временной области  ). Частотная характеристика формирующего фильтра определяется из соотношения
). Частотная характеристика формирующего фильтра определяется из соотношения  . Пусть
. Пусть 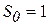 , тогда
, тогда  .
.
Дифференциальное уравнение формирующего фильтра:
 (**)
(**)
2. Эквивалентная система есть соединение (*) и (**) и имеет второй порядок. Вектор состояния  . Тогда система (*) и (**) имеет вид
. Тогда система (*) и (**) имеет вид
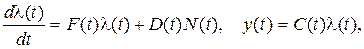 где
где  ,
,
 ,
,  .
.
Интенсивность белого шума  .
.
Матрица ковариаций в общем случае  .
.
В нашем случае  .
.
 .
.
3. Уравнение для  :
:
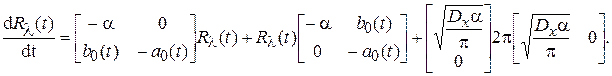
Подставим выражение  с учетом
с учетом  .
.
 .
.
Соответственно три уравнения:

Последние два уравнения можно моделировать.
|
из
5.00
|
Обсуждение в статье: Определение корреляционной функции и дисперсии через спектральную плотность входного сигнала |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


 .
.