 |
Главная |
Марковские случайные процессы
|
из
5.00
|
(Марков Андрей Андреевич старший, 1856–1922 г.г.).
В зависимости от непрерывного или дискретного tÎ[0, T] и случайной величины x (t) различают 4 основных вида Марковских случайных процессов:
1. Марковские цепи (дискретный случайный процесс с дискретным временем).
2. Дискретный Марковский процесс (дискретный случайный процесс с непрерывным временем).
3. Марковские последовательности (непрерывный случайный процесс с дискретным временем).
4. Непрерывнозначный Марковский процесс (непрерывный случайный процесс с непрерывным временем).
Определение. Случайный процесс x (t) называется Марковский, если для любых n моментов времени t1< t2<…<tn из отрезка Î[0, T] условная функция распределения «последнего» значения x (tn) при фиксированных x(t1), xt2) ,…, x (tn -1) зависит только от x (tn -1), т.е. при заданных значениях x1, x2 ,…, xn -1 справедливо соотношение
P{x (tn) £ xn | x (t1) = x1, x(t2) = x2 ,…, x( tn -1) = xn -1 }=
= P {x (tn) £ xn|x (tn -1) = xn -1}. (1)
Для трех моментов времени tk < tj <ti (1) принимает вид
P {x (ti) £ xi | x (tk) = xk, x( tj) = xj }=
= P {x (ti) £ xi |x( tj) = xj}. (2)
Таким образом, если точно известно состояние Марковского процесса (МП) в момент времени tj , будущее (при ti) и прошлое (при tk) состояния МП независимы.
Другое определение. Для tk < tj <ti
{x (ti) £ xi, x (tk) £ xk | x( tj) = xj}=
= P {x (ti) £ xi | x( tj) = xj}× P {x (tk) £ xk | x( tj) = xj}, (3)
Это определение симметричное относительно времени и означает, что при фиксированном состоянии случайного процесса в настоящий момент времени tj будущее (при ti) и прошлое (при tk) состояния Марковского процесса независимы.
Другое важное свойство: эволюция вероятности перехода
P {x (t) £ x | x( t0) = x0}описывается уравнением вида dP/dt = AP, (4)
где А – некоторый линейный оператор (матрица, дифференциальный оператор и др.). Тогда можно использовать методы дифференциальных уравнений.
Пусть заданы начальные условия в начальный момент t0 . Тогда при отсутствии каких-либо ограничений нужно записать решение (4) и, при задании начальных условий, найти решение.
Если же имеются еще и ограничения (граничные условия), то нужно при нахождении решения использовать их.
Например, точка, отражающая поведение системы, начиная движение из начального состояния x( t0) = x0, при достижении границы x( t) = С «поглощается» ею и работа системы прекращается (нарушается) (траектория 1); точка «отражается от границы» (траектория 2) и т.д.

Если граница поглощающая, то помимо отыскания вероятности перехода Р для x < С, можно интересоваться вероятностью «поглощения» за некоторое Т или же математическим ожиданием, дисперсией и другими характеристиками времени Т, когда траектория впервые достигает границы С.
Задачи указанного характера имеют математически строгое решение только для Марковского процесса.
1. Простая цепь Маркова. Пусть случайный процесс  принимает конечное число K различных дискретных значений v1, v2, …, vk в некоторые моменты t0 <t1 < t2 …< tN. Эти значения могут мгновенно изменяться, т.е. имеют место переходы vi ® vj i, j =
принимает конечное число K различных дискретных значений v1, v2, …, vk в некоторые моменты t0 <t1 < t2 …< tN. Эти значения могут мгновенно изменяться, т.е. имеют место переходы vi ® vj i, j = 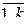 .
.
Характерное свойство простой цепи Маркова состоит в том, что
ver Р 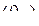 значения процесса
значения процесса 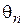 в момент tn зависит лишь от того , какое значение имел процесс в непосредственно предшествующий ему момент времени tn –1 и не зависит от значений процесса в более ранние моменты времени, т.е
в момент tn зависит лишь от того , какое значение имел процесс в непосредственно предшествующий ему момент времени tn –1 и не зависит от значений процесса в более ранние моменты времени, т.е  .
.
Поэтому для простой цепи Маркова совместные конечномерные цепи Маркова вычисляются как:
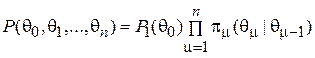 . (5)
. (5)
Условные вероятности 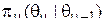 принято называть вероятностями перехода из состояния
принято называть вероятностями перехода из состояния 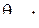 в состояние
в состояние  за промежуток времени
за промежуток времени 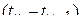 .
.
Одна из основных задач в теории простых цепей Маркова:
Пусть задано начальное значение случайного процесса при  и указан вероятностный закон смены соседних значений СП (т.е. заданы ver перехода).
и указан вероятностный закон смены соседних значений СП (т.е. заданы ver перехода).
Каким образом можно найти вероятности различных значений СП в момент времени 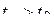 и, в частности, при
и, в частности, при  ?
?
Введем обозначения для безусловных и условных вероятностей:  (6)
(6)
Величина  есть безусловная вероятность значения
есть безусловная вероятность значения 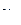 на n-м шаге (при
на n-м шаге (при 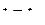 ), а
), а 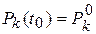 начальное вероятностное значение
начальное вероятностное значение 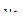 .
.
Условная вероятность 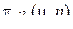 определяет вероятность значения
определяет вероятность значения 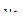 при
при  , если в более ранний момент времени
, если в более ранний момент времени 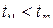 значение СП было равно
значение СП было равно 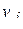 .
.
Эти вероятности неотрицательны и удовлетворяют условию нормировки:
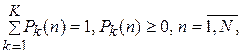 (7)
(7)
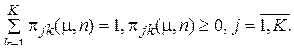 (8)
(8)
На основании правила полной вероятности получаются уравнения Маркова:
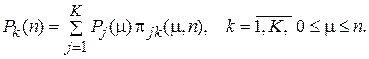 (9)
(9)
Выполняется:
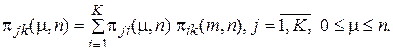 (10)
(10)
Среди простых цепей Маркова выделяются однородные цепи, где вероятности перехода 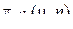 зависят лишь от разности аргументов, т.е.
зависят лишь от разности аргументов, т.е.
 (11)
(11)
Обозначим одношаговые вероятности перехода через 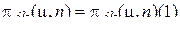 .
.
Полное вероятностное описание простой однородной цепи Маркова достигается заданием начальных вероятностей 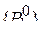 и матрицы одношаговых вероятностей перехода
и матрицы одношаговых вероятностей перехода
 . (12)
. (12)
Таким образом, для простой однородной цепи Маркова матрица вероятностей перехода за n шагов равна
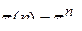 (13)
(13)
а матрица вероятностей различных значений СП:
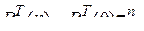 (14)
(14)
где 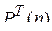 - матрица-строка безусловных вероятностей различных значений СП на
- матрица-строка безусловных вероятностей различных значений СП на 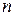 -м шаге;
-м шаге;  при шаге
при шаге  .
.
Однородная цепь Маркова, для которой вероятности 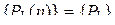 , т.е. не зависит от
, т.е. не зависит от 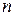 называется стационарной, в противном случае - нестационарной.
называется стационарной, в противном случае - нестационарной.
В общем случае 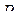 , если они существуют, находятся в результате предельного перехода
, если они существуют, находятся в результате предельного перехода
 (15)
(15)
и называются финальными вероятностями.
Если 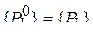 - стационарная цепь Маркова начинается с
- стационарная цепь Маркова начинается с  .
.
Финальные вероятности должны удовлетворять системе k линейных алгебраических уравнений
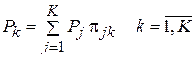 (16)
(16)
и дополнительно условию
 (17)
(17)
Если взять 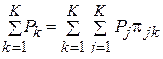 и, учитывая (8), т.е.
и, учитывая (8), т.е. 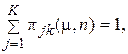 приходим к тождеству.
приходим к тождеству.
Поэтому k уравнений в (16) являются линейно зависимыми, и k финальных вероятностей следует определять из (k -1) уравнений (16) уравнения (17).
2. Дискретный марковский процесс.
Пусть 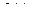 по-прежнему принимает только дискретные значения
по-прежнему принимает только дискретные значения
v1, v2, …, vk ,но смена этих значений происходит не в фиксированные, а в любые случайные моменты времени. Вероятности перехода
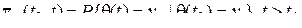 (18)
(18)
Удовлетворяют следующим соотношениям
 , (19)
, (19)
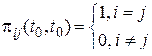 . (20)
. (20)
Кроме того, для них справедливо уравнение Колмогорова-Чэпмена:
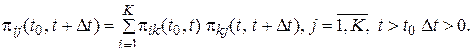 (21)
(21)
Характерное свойство: для малых  вероятность
вероятность 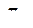 того, что значение не изменится, превышает вероятность изменения значения:
того, что значение не изменится, превышает вероятность изменения значения:
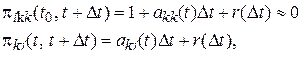 (22)
(22)
так как вероятность перехода из одного значения в другое неотрицательны, т.е. 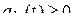 , и для них должно выполняться условие нормировки (19), то из (22) получаем
, и для них должно выполняться условие нормировки (19), то из (22) получаем
 (23)
(23)
В (22)  .
.
Подставляя (22) в (21) и  получим систему линейных дифференциальных уравнений
получим систему линейных дифференциальных уравнений
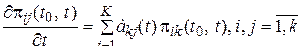 , (24)
, (24)
где 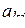 (t)удовлетворяет (23). Решение этой системы при начальных условиях (20)дает зависимость вероятностей перехода от времени.
(t)удовлетворяет (23). Решение этой системы при начальных условиях (20)дает зависимость вероятностей перехода от времени.
Замечания. Дискретный марковский процесс остается марковским и в обратном направлении, т.е. наряду с (24) (прямые дифференциальные уравнения) справедливы обратные уравнения
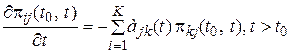 . (25)
. (25)
Уравнениям (24) удовлетворяют не только вероятности перехода, но и безусловные вероятности значений  (t):
(t):
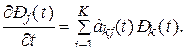 (26)
(26)
Их нужно интегрировать при начальных условиях
 (t)=
(t)=  . (27)
. (27)
Дискретный марковский процесс называется однородным, если вероятности перехода 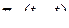 зависят только разности
зависят только разности 
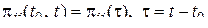 . (28)
. (28)
Если при  существует
существует 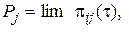 которые не зависят от начального состояния, то марковский процесс – стационарный марковский процесс, и вероятности стационарных значений определяются системой алгебраических уравнений:
которые не зависят от начального состояния, то марковский процесс – стационарный марковский процесс, и вероятности стационарных значений определяются системой алгебраических уравнений:
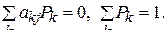 (29)
(29)
3. Марковские последовательности(МП).
Пусть случайные величины 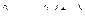 в некоторые дискретные моменты времени t1 < t2 …< tn …< tN принимают непрерывные множества возможных значений.
в некоторые дискретные моменты времени t1 < t2 …< tn …< tN принимают непрерывные множества возможных значений.
Определяющее свойство марковской последовательности 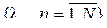 состоит в том, что совместная плотность вероятности рассматриваемых случайных величин выражается через плотность вероятности начального состояния
состоит в том, что совместная плотность вероятности рассматриваемых случайных величин выражается через плотность вероятности начального состояния 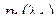 и плотности вероятности перехода
и плотности вероятности перехода 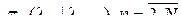 :
:
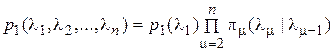 . (31)
. (31)
Основные свойства марковской последовательности:
1. Если точно известно значение МП в настоящий момент t, то ее будущее значение не зависит от предыдущего состояния.
2. Любая последовательность, взятая из марковской, является также марковской.
3. МП остается марковской и в обратном направлении.
4. Плотность вероятности перехода удовлетворяет уравнению
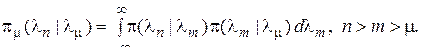 (32)
(32)
МП называется однородной, если плотности ver перехода 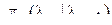 не зависят от n .
не зависят от n .
МП называется стационарной, если она однородна и все случайные величины  имеют одну т ту же плотность вероятности:
имеют одну т ту же плотность вероятности:  .
.
4. Непрерывнозначный марковский процесс (НМП).
Область значений непрерывнозначного процесса  и область его определения [0, T] есть непрерывные множества. Для НМП диффузного типа плотность ver перехода
и область его определения [0, T] есть непрерывные множества. Для НМП диффузного типа плотность ver перехода  и безусловная плотность вероятности
и безусловная плотность вероятности 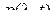 удовлетворяет уравнению в частных производных Фоккера-Планка-Колмогорова, которое применительно к плотности ver
удовлетворяет уравнению в частных производных Фоккера-Планка-Колмогорова, которое применительно к плотности ver 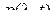 имеет вид:
имеет вид:
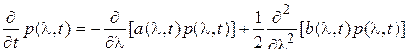 , (33)
, (33)
или иначе,
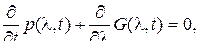 (34)
(34)
где
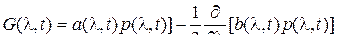 . (35)
. (35)
«Коэффициенты» сноса  и диффузии
и диффузии 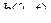 определяются по исходному стохастическому дифференциальному уравнению, описывающему поведение рассматриваемой системы, в виде:
определяются по исходному стохастическому дифференциальному уравнению, описывающему поведение рассматриваемой системы, в виде:
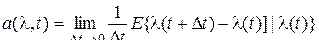 , (36)
, (36)
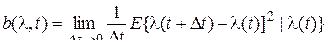 . (37)
. (37)
Если стохастическое дифференциальное уравнение имеет вид
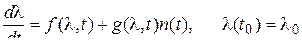 , (38)
, (38)
где  и – детерминированные формы своих аргументов, – (гауссовский) белый шум с нулевым математическим ожиданием и корреляционной функцией
и – детерминированные формы своих аргументов, – (гауссовский) белый шум с нулевым математическим ожиданием и корреляционной функцией
 , (39)
, (39)
то коэффициенты сноса и диффузии равны
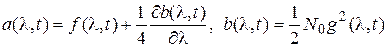 . (40)
. (40)
Коэффициент сноса  характеризует среднее значение локальной скорости МП , а коэффициент диффузии
характеризует среднее значение локальной скорости МП , а коэффициент диффузии 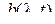 – локальную скорость изменения дисперсии (приращения). Если плотность ver перехода зависит лишь от разности временных аргументов
– локальную скорость изменения дисперсии (приращения). Если плотность ver перехода зависит лишь от разности временных аргументов  , а коэффициенты a и b не зависят от
, а коэффициенты a и b не зависят от  и
и  , то рассматриваемый процесс
, то рассматриваемый процесс 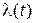 называется однородным во времени.
называется однородным во времени.
При начальных условиях 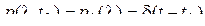 безусловная плотность вероятности
безусловная плотность вероятности 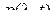 совпадает с плотностью вероятности перехода
совпадает с плотностью вероятности перехода 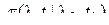 . При этом решение уравнения Фоккера-Планка-Колмогорова (ФПК) (33) называется фундаментальным решением.
. При этом решение уравнения Фоккера-Планка-Колмогорова (ФПК) (33) называется фундаментальным решением.
Для отыскания решения ФПК(33) необходимо задать начальное условие  (41)
(41)
и указать граничные условия.
Граничные условия могут быть весьма разнообразными и определяются существом физической задачи.
Приведем три вида:
1. Если случайный процесс 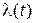 может принимать всевозможные значения от
может принимать всевозможные значения от 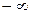 до
до 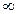 , то обычно выполняются нулевые граничные условия
, то обычно выполняются нулевые граничные условия
 . (42)
. (42)
2. Если случайный процесс 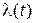 может принимать значения лишь в ограниченном интервале (c, d), причем в точках c, d помещены отражающие границы: траектория на них зеркально отражается. Тогда выполняются условия отражения границ:
может принимать значения лишь в ограниченном интервале (c, d), причем в точках c, d помещены отражающие границы: траектория на них зеркально отражается. Тогда выполняются условия отражения границ:
 .
.
3. В точках c, d расположены поглощающие границы: траектория на них поглощается и исключается из рассмотрения. Тогда должны выполняться условия поглощения:
 .
.
|
из
5.00
|
Обсуждение в статье: Марковские случайные процессы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

