 |
Главная |
Задача оптимальной фильтрации
|
из
5.00
|
Пусть измеренный сигнал x(t) является функцией полезного сигнала s(t)и шума n(t), т.е.
x(t) = f(s(t, λ(t), n(t)), (1)
λ(t) – есть в общем случае совокупность параметров; вид f(×××) должен быть известен.
Наиболее часто в задачах фильтрации используется критерий минимума среднего квадрата ошибки, критерий минимального отношения сигнал/шум и критерий максимума апостериорной вероятности.
Рассмотрим минимум среднего квадрата ошибки в линейной постановке.
Предполагаем, что имеет место аддитивность s(t) и n(t)
x(t) = s(t, λ(t)) + n(t).
Пусть s(t) = s[t, λ(t)] и n(t) – стационарные нормальные случайные процессы с известными ковариационными функциями:
Rs(τ)=E[s(t), s(t + τ)], Rn(τ)=E[n(t), n(t + τ)], Rsn (τ)=E[s(t), n(t + τ)].
Требуется определить систему, которая из измеренной смеси
x(t) = s(t) + n(t)
выделяет полезный сигнал.
Таким образом, искомая оптимальная система фильтрации должна минимизировать величину
 . (2)
. (2)
Здесь для общности введен временной сдвиг D; при D > 0  является прогнозом s(t); при D = 0 задача сводится к выделению (сглаживанию) сигнала s(t) из измеренного х(t).
является прогнозом s(t); при D = 0 задача сводится к выделению (сглаживанию) сигнала s(t) из измеренного х(t).
Задача имеет строгое решение на полубесконечном интервале (– ∞, t) (А.Н. Колмогоров (1941), Н. Винер (1949)) в виде линейного фильтра с постоянными параметрами.
Пусть на входе физически реализуемой линейной системы с импульсной характеристикой
 (условие физической реализуемости) (3)
(условие физической реализуемости) (3)
Имеется стационарный случайный процесс x(t) . При этом стационарный случайный процесс y(t)=  .
.
Пусть
 . (4)
. (4)
Подставляя (4) в (2), получим
 (5)
(5)
где
Rsx(τ)=E[s(t), x(t + τ)], (6)
Rx(τ)=E[x(t), x(t + τ)]. (7)
Вопрос: как определить оптимальную g0(t)?
Используется прием вариационного исчисления (также основная лемма вариационного исчисления), а именно:
Пусть
g(t)= g0(t)+µh(t), (8)
µ – параметр, скаляр;
h(t) – вариация в окрестности g0(t), причем h(t1) = h( t2). Здесь t1 = 0, t2 =∞.
Тогда условие min 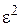 задается в виде
задается в виде
 . (9)
. (9)
Подставляя (8) в (5), получим

 .
.
Тогда из последнего уравнения следует
 - (10)
- (10)
уравнение Фредгольма I рода, или уравнение Винера-Хопфа, решением которого и является g0(t).
Решение (10) встречает ряд трудностей, в основном с требованиями физической реализуемости оптимального фильтра. В частном случае, когда Sx(w) - дробно-рациональная функция из (10) получается передаточная функция оптимального фильтра:
 . (11)
. (11)
 Здесь
Здесь 
Минимальный средний квадрат оптимальной фильтрации:
 , (12)
, (12)

Замечание. Условие физической реализуемости (3) может не обеспечить наилучшей точности выводов (11), (12).
Пример.
Пусть x(t) = s(t) + n(t), где s(t) – статистически независимо от n(t).
Пусть Sn(w)=N0/2, wÎ(-∞, ∞), Ss(w) =  , wÎ(-∞, ∞).
, wÎ(-∞, ∞).
Найти

Поскольку s(t) и n(t) независимы, то

Тогда

В результате

.
Вычисление  имеет сложный характер и окончательно имеет вид:
имеет сложный характер и окончательно имеет вид:
 .
.
Тогда




где

В общеупотребительном виде (при D = t) фильтр Винера

где [×]+– означает рассмотрение оператора с полюсами в левой полуплоскости.
Особенности. Полученный фильтр оптимален для сигналов с гауссовым распределением.
1. Должна быть задана априорная информация о сигнале и шуме в терминах корреляционных функций и спектральных плотностей. При этом должная выполняться факторизация  .
.
2. Описание этого фильтра недостаточно хорошо подходит для цифровых вычислений.
3. Синтез реального фильтра  может оказаться совсем не простым.
может оказаться совсем не простым.
4. Метод не распространяется на нестационарные сигналы.
5. Метод может быть распространен на многомерный случай.
|
из
5.00
|
Обсуждение в статье: Задача оптимальной фильтрации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

