 |
Главная |
Пример графического решения задачи
|
из
5.00
|
Найдем оптимальное решение задачи, математическая модель которой имеет вид


Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис.2.2).
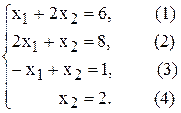
(1) – 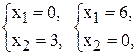 (2) –
(2) – 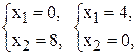 (3) –
(3) – 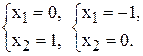
Прямая (4) проходит через точку  параллельно оси
параллельно оси  .
.

Рис.2.2. Графическое решение задачи
Решение с использованием Симплекс-метода
Основная идея метода – оптимальное решение находится в одной из вершин многогранника, описанного системой ограничений. Наша задача – найти, в какой именно вершине.
Для решения используют преобразование ЗЛП к канонической форме:
1. Целевая функция минимизируется
2. Все ограничения имеют вид равенств
3. Свободные члены (B) в ограничениях неотрицательны
4. Все переменные неотрицательны
Преобразование ЗЛП к канонической форме реализуется через следующий алгоритм:
1. Если целевая функция исходной задачи максимизируется, то она умножается на (–1) и минимизируется.
2. Если ограничение имеет вид неравенства, то вводится фиктивная неотрицательная переменная xn + l , которая добавляется к ограничению (если оно имеет вид «меньше или равно» или же вычитается (если ограничение имеет вид «меньше или равно»)
3. Если bi отрицательна, то i -е ограничение умножается на -1
4. Если на переменную не наложено условие неотрицательности, то она представляется как разность двух неотрицательных переменных.
ЗЛП в канонической форме:
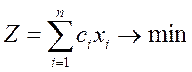 – целевая функция
– целевая функция
ограничения:

В матричной форме:

Затем составляется симплексная таблица:
Таблица 2.2
Исходная таблица для решения задачи Симплекс-методом
|
| Свободные переменные | Свободные члены | ||||
| x1 | x 2 | … | xn | |||
| Базисные (фиктивные переменные) | xn+1 | a11 | a12 | … | a1n | b1 |
| xn+2 | a21 | a22 | … | a2n | b2 | |
| … | … | … | … | … | … | |
| xn+l | an1 | an2 | … | ann | bn | |
| Коэффициенты при целевой функции | c1 | c2 | … | cn | Z | |
Затем путем последовательных преобразований получают таблицу, в которой в последнем столбце получают положительные числа. Значения свободных переменных (факторов) будут находиться в столбце свободных членов.
Подробнее о реализации этого метода можно прочитать в дополнительной литературе (см. список литературы).
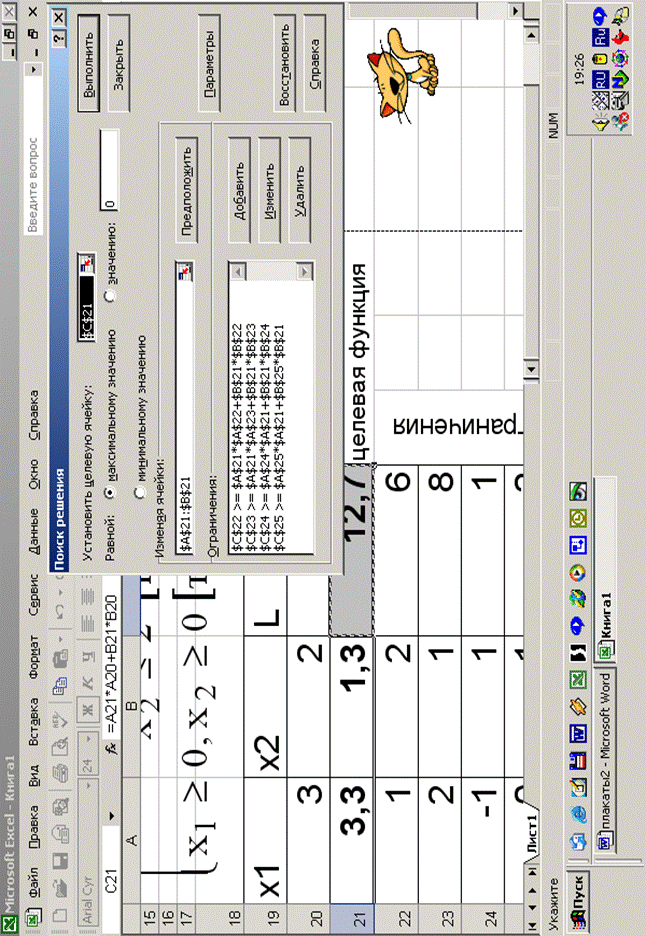
3. Численное решение с использованием компьютерных программ:
Транспортная задача
Стандартная транспортная задача определяется как задача разработки наиболее экономичного плана перевозки продукцииодного вида из нескольких пунктов отправления в несколько пунктов назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.
Исходные параметры модели ТЗ
1) n – количество пунктов отправления, m – количество пунктов назначения.
2) 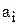 – запас продукции в пункте отправления
– запас продукции в пункте отправления 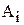 (
(  ) [ед. прод.].
) [ед. прод.].
3)  – спрос на продукцию в пункте назначения
– спрос на продукцию в пункте назначения 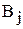 (
( 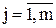 ) [ед. прод.].
) [ед. прод.].
4)  – тариф (стоимость) перевозки единицы продукции из пункта отправления
– тариф (стоимость) перевозки единицы продукции из пункта отправления 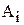 в пункт назначения
в пункт назначения 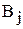 [ден.ед./ед. прод.].
[ден.ед./ед. прод.].
Искомые параметры модели ТЗ
1)  – количество продукции, перевозимой из пункта отправления
– количество продукции, перевозимой из пункта отправления  в пункт назначения
в пункт назначения 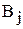 [ед. прод.].
[ед. прод.].
2) 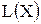 – транспортные расходы на перевозку всей продукции [ден.ед.].
– транспортные расходы на перевозку всей продукции [ден.ед.].
Этапы построения модели
I. Определение переменных.
II. Проверка сбалансированности задачи.
III. Построение сбалансированной транспортной матрицы.
IV. Задание ЦФ.
V. Задание ограничений.
Вид транспортной модели
 ;
;
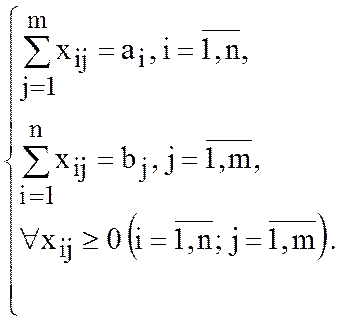
Транспортная задача называется сбалансированной, если:
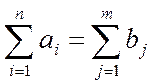 ,
,
если равенство не выполняется, то необходимо:
1) если  вводится фиктивный пункт назначения со спросом, равным:
вводится фиктивный пункт назначения со спросом, равным:  и с затратами на доставку в него, равными либо 0, либо штрафу за недоотправление.
и с затратами на доставку в него, равными либо 0, либо штрафу за недоотправление.
2) если  вводится фиктивный пункт отправления с запасом, равном:
вводится фиктивный пункт отправления с запасом, равном: 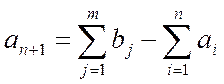 и с затратами на доставку из него, либо равными 0, либо штрафу за недоотправку.
и с затратами на доставку из него, либо равными 0, либо штрафу за недоотправку.
Сбалансированная транспортная матрица будет иметь вид:
Таблица 2.3
Общий вид транспортной матрицы
| Пункты отправления, | Пункты потребления, | Запасы,
| |||
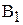
| 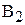
| … | 
| ||
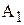
|  , ,
| 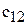
| … | 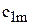
| 
|

| 
| 
| … | 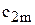
| 
|
| … | … | … | … | … | … |
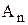
| 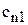
| 
| … | 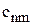
| 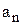
|
| Потребность | 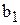
| 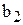
| … | 
| 
|
Этапы решения модели:
I. Определение опорного плана
II. Нахождение оптимального решения
I . Опорный план является допустимым решением транспортной задачи и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов:
¨ метод северо-западного угла;
¨ метод минимального элемента;
¨ метод Фогеля.
«Качество» опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла – наихудшее.
Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода.
|
из
5.00
|
Обсуждение в статье: Пример графического решения задачи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

