Базовая модель управления запасами (Модель Уилсона)

 

Рис. 5.2 «Черный ящик» модели Уилсона

 

Допущения модели Уилсона:

1. Величина спроса (интенсивности потребления запаса) постоянна (ν=const)

2. Затраты на формирование заказа постоянны и не зависят от размера заказа (K=const)

3. Затраты на хранение единицы запаса постоянны (s=const)

4. Дефицит недопустим (Q≥0)

5. Пополнение заказа осуществляется мгновенно

 

Вывод уравнений модели:

Расчетные формулы модели Уилсона:

1.

 

2.

 

3.

 

4.

 

Рис. 5.3 Цикл изменения запасов в модели Уилсона

 

 

Модель экономичного размера партии

Часто в экономических системах пополнение запаса осуществляется не мгновенно, а с конечной интенсивностью (λ). Пример – производственный процесс, состоящий из двух станков:

 

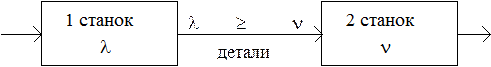
Рис. 5.4 Производственный процесс, состоящий из двух станков

 

В этом случае модель управления запасами претерпит изменения:

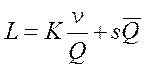, где  – средний размер запаса на складе

, где Q_max – максимальный размер запаса на складе.

 

Таким образом, расчетные формулы имеют вид:

1.       2.

3.   

Рис. 5.5 Изменение уровня запасов в модели планирования экономичного размера партии

 

5.4 Модель планирования дефицита

В экономических системах, связанных со сбытом продукции, дефицит, как правило, допустим.

Возможны два варианта:

1) отказ от выполнения заявки на отсутствующий товар – приводит к потерям возможной прибыли от реализации товара;

2) отсрочка выполнения заказа и его выполнения, когда запас пополнится – связано с предоставлением более льготных, по сравнению с немедленной продажей, условий (более низкая цена и т.п.)

В этом случае задача управления запасами – установить размер партии заказа, минимизирующий затраты на управление запасами с учетом штрафа за отсутствие запаса (g).

 

Расчетные формулы:

 

1.         

2.

3.   

 

Если заказ пополняется немедленно:

1.     

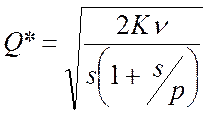
2.

3.   

 

Рис. 5.6 Цикл изменения запасов в модели планирования дефицита

 

 

Модель, учитывающая скидки

, где C =( p - p ₁ ) – размер скидки

 

 

Алгоритм:

1. Определить Q_w – оптимальный размер заказа по модели Уилсона

2. Если  (область I), где Q_p1 – точка разрыва цен

 

L

 

C

 

 

 

 

I область                                      II область                          III область

 

                                                                       Q

 

Рис. 5.7.

то  ;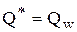

иначе найти значение 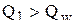, при котором общие затраты, рассчитанные для цен C и  совпадают, для этого решить уравнение .

 

3. Если  (область II),

L

 

C

 

 

 

I область                                      II область                         III область

                                                     Q

 

то .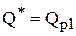

4. Если  (область III),

L

 

C

 

 

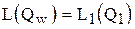
I область                                                           II область                         III область

 

                                              Q

 

то .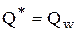

 

так повторить для каждой скидки

таким образом,

 

 

Список литературы

1. Альсевич В.В. Математическая экономика. Конструктивная теория: Учеб. пособие. – Минск: Изд-во Дизайн ПРО, 1998. – 238 с. (1470255-ООЛ)

2. Амелькин Д.В. Дифференциальные уравнения в приложениях. - М.: Наука, 1978. -92 с.

3. Ашманов С.А. Введение в математическую экономику: Учеб. пособие. - М.: Наука, 1984. - 293 с.

4. Ашманов С.А. Математические методы и модели в экономике: Учеб. пособие. - М.: Изд-во МГУ, 1980. – 199 с. (1104962-ООЛ)

5. Багриновский К.А., Бусыгин В.П. Математика плановых решений. - М.: Наука, 1980.

6. Большие системы: моделирование организационных механизмов/ В.Н. Бурков и др. - М.: Наука, 1989.

7. Букан Дж., Кенинсберг Э. Научное управление запасами. М.: Наука, 1967.

8. Вагнер Г. Основы исследования операций, 1-3 т. - М.:, 1972-73.

9. Вайну Я. Я.-Ф. Корреляция рядов динамики. - М.: "Статистика", 1977 г. - 119 с.

10. Варфоломеев В.И., Назаров С.В., Алгоритмическое моделирование элементов экономических систем: Практикум. – М.: Финансы и статистика - 2004, 263 стр.

11. Вентцель Е.С. Исследование операций. М, Советское радио, 1972.

12. Воркуев Б.Л., Анализ решений экономико-математических моделей. М., изд. МГУ, 1987.

13. Воркуев Б.Л., Грачева М.В., Лукаш Е.Н. Математические методы анализа экономики. Модель межотраслевого баланса. М., изд. МГУ, 1990.

14. Высшая математика для экономистов: Учебник для вузов/ Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. Кремера Н.Ш. - М.: ЮНИТИ, 2000. - 471 с.

15. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие для студентов вузов -6-е изд. - М.: Высшая школа, 2002. -405с.

16. Годунов С.К., Рябенький В.С. Разностные схемы. Введение в теорию. - М.: Наука, 1977. -

17. Горчаков А.А., Орлов И.В. Компьютерные экономико-математические модели. -М.: ЮНИТИ, 1995. - 134 с. (1451168-КХ)

18. Гранберг А.Г. Математические модели социалистической экономики. Учебное пособие для экон. вузов и фак. - М.: Экономика, 1978. - 351 с.

19. Гранберг А.Г. Моделирование социалистической экономики. М., Экономика, 1988.

20. Губин Н.М., Добронравов А.С., Дорохов Б.С. Экономико-математические методы и модели в планировании и управлении в отрасли связи. М., Радио и связь, 1993.

21. Дробушевич В.И., Дымников В.П., Ривин Г.С. Задачи по вычислительной математике. - М.: Наука, 1980. - 144 с.

22. Ермольев Ю.М. и др. Математические методы исследования операций. Учебное пособие для вузов. - Киев, "Вища школа", 1979. - 312 с.

23. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: Изд-во ДИС, 1998. - 365 с.

24. Иванилов Ю.П., Лотов А.В. Математические модели в экономике: Учеб. пособие. – М: Наука, 1979. - 303 с.

25. Интриллигатор М. Математические методы оптимизации и экономическая теория. – М.: Изд-во Прогресс, 1975. – 605 с. (938168-ООЛ)

26. Исследование операций в экономике Учебное пособие для вузов./ Под ред. Н.Ш. Кремера - М.: ЮНИТИ, 2000. -407 с.

27. Калихман И. Л., Войтенко Динамическое программирование в примерах и задачах: Учебное пособие. - М.: Высшая школа, 1979. - 125 с., ил.

28. Калихман И.Л. Сборник задач по математическому программированию. - М.: Высшая школа, 1975. - 270 с.

29. Карасев А.И., Кремер Н.Ш., Савельева Т.И. Математические методы и модели в планировании: Учеб. пособие для эконом. вузов. - М.: Экономика, 1987.

30. Катулев А.Н., Северцев Н.А. Исследование операций: принципы принятия решений и обеспечение безопасности. М., Наука, 2000.

31. Колемаев В.А. Математическая экономика. Учебник для вузов -М.: ЮНИТИ, 1998. -240с

32. Конюховский П. Математические методы исследования операций в экономике. – СПб.: Питер, 2000г.

33. Коршунова Н.И., Плясунов В.С. Математика в экономике. - М.: Вита-Пресс, 1996.

34. Коссов В.В. Межотраслевые модели (теория и практика использования). М., Экономика, 1973.

35. Кремер Н.Ш. Теория вероятностей и математическая статистика. Учебник для вузов. - М.: ЮНИТИ-ДАНА, 2001 г. - 543 с.

36. Кремер Н.Ш., Путко Б.А. Исследование операций в экономике. Учебное пособие. – М.: ЮНИТИ, 2004, 407 стр

37. Крушевский А.В. Справочник по экономико-математическим моделям и методам. - К.: Техника, 1982. - 208 с.

38. Крыньский Х.Э. Математика для экономистов. - М.: Статистика, 1970.

39. Кузьмин П.И. Симплекс-метод для решения задач линейного программирования. Методические указания для студентов-математиков. - Барнаул: Изд-во АГУ, 1987. - 16 с.

40. Куликов Ю.Г., Шеховцова Н.Ф., Зикеева Л.П. Экономико-математические методы и модели: Учеб. пособие для практических занятий. – М.: МПСИ, 2000. – 89 с. (1483654-КХ)

41. Курош А.Г. Курс высшей алгебры. - М.: Наука, 1975. - 432 с.

42. Кухарев В.Н., Салли В.И., Эрперт А.М. Экономико-математические методы и модели в планировании и управлении: Учебник. - Киев: Выща школа, 1991. - 300 с. (1413380-КХ)

43. Лагоша Б.А., Шаркович В.Г., Дегтярева Т.Д. Методы и модели совершенствования организационных структур. Наука, 1988. Москва

44. Леонтьев В.В. Экономическое эссе: теории, исследования, факты и политика. - М., Политиздат, 1990. - 414 С.

45. Лившиц А.Л. Статистическое моделирование систем массового обслуживания. М.: 1978 г.

46. Линейное программирование (коллектив авторов). - М., 1961.

47. Линник Ю.Б. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. - М.: Гос. издат. Физ.-мат.лит., 1958. - 334 с.

48. Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений: Учебное пособие для вузов. - М.: Финансы, ЮНИТИ, 1998. - 400 с.

49. Малыхин В.И. Математика в экономике: Учебное пособие -М.: ИНФРА-М, 1999. -356с.

50. Малыхин В.И. Математическое моделирование экономики. Учебно-практическое пособие для ВУЗов / УРАО. - М.: Изд-во УРАО, 1998. - 160 с.

51. Математическая экономика на ПК /под ред. Кубонива М. М., ФиС, 1991.

52. Математические методы в экономике: Учебник. 2-е изд./Замков О.О., Толстопятенко А.В., Черемных Ю.Н. -М.: МГУ им. М.В. Ломоносова, "Дело и Сервис", 1999. -368 с.

53. Математический энциклопедический словарь (гл. редактор Прохоров Ю.В.). - М.: Советская энциклопедия, 1988.

54. Математическое моделирование. Под ред. Дж. Эндрюса и Р. Мак-Лоуна. Пер с англ. Ю.П. Гупало. - М.: Мир, 1979 - 279 с.

55. Моделирование народнохозяйственных процессов /под ред. Дадаяна В.С. М., 1972.

56. Моделирование народнохозяйственных процессов /под ред. Котова И.В. Л., изд. ЛГУ, 1990.

57. Моделирование народно-хозяйственных процессов. Учебное пособие для экон. вузов и фак. под ред. Дадаяна В.С. - М.: Экономика, 1973. - 479 с.

58. Моисеев Н.Н. и др. Методы оптимизации, Наука, 1978. - 352 с.

59. Назаров А.А. Управление системами массового обслуживания и их оптимизация. - Томск, 1984 г.

60. Нейлор Т. Машинные имитационные эксперименты с моделями экономических систем. Пер. с англ. - М.: Мир, 1975 - 500 с.

61. Овсиенко Ю.В., Леонтьев В.В. Межотраслевая экономика. // Экономика и математические методы. - 1998. - ©3.

62. Овчаренко Е. К., Ильина О.П., Балыбердин Е. В. Финансово-экономические расчёты в EXCEL. - М.: Информационно-издательский дом "Филинъ", 1997 - 152 с.

63. Орлов И.В. Экономико-математические методы и модели. Выполнение расчетов в среде EXCEL: Практикум- М.: Финстатинформ, 2000. - 135 с. (1483105-КХ)

64. Плоткин Б.К. Экономико-математические методы и модели в управлении материальными ресурсами: Учеб. пособие. – СПб.: Изд-во СПб. ун-та экономики и финансов, 1992. – 63 с.

65. Поляк Б.Т. Введение в оптимизацию. М., Наука, 1983.

66. Сборник задач по дифференциальным уравнениям. А.Ф. Филиппов. - М.: Наука, 1979. - 128 с.

67. Сетевое планирование и управление. Под ред. Д.И.Голенко. М., Экономика, 1967.

68. Сетевые графики в планировании. Под ред. Разумова. М., Высшая школа, 1975.

69. Солодовников А. С., Бабайцев В.А., Браилов А.В. Математика в экономике: Учебник. - М.: Финансы и статистика, 1998. - 218 с.

70. Спирин А.А., Фомин П.П. Экономико-математические методы и модели в торговле.: Учебное пособие. - М., "Экономика", 1988. - 145 с.

71. Столерю Л. Равновесие и экономический рост. М., Наука, 1974.

72. Суспицын С.А. Общие модели экономики и экономическая реформа (опыт аксиоматических построений). Препринт. Новосибирск: ИЭиОПП СО РАН, 1991.

73. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. М., Наука, 1986.

74. Тарасевич В.М. Экономико-математические методы и модели в ценообразовании: Учебник. -Л.: Изд-во ЛФЭИ, 1991. - 178 с.

75. Таха X. Введение в исследование операций. М.: Мир, 1985.

76. Терехов Л.Л. Экономико-математические методы: Учеб. пособие для эконом. вузов. - М.: Статистика, 1972.

77. Терехов Л.Л., Куценко В.А., Сиднев С.П. Экономико-математические методы и модели в планировании и управлении. - Киев.: Выща школа, 1979.

78. Уткин Э.А. Цены и ценообразование. Ценовая политика. М., Изд-во ЭКМОС, 1997г. - 224с.

79. Федосеев В.В. и др., Экономико-математические методы и прикладные модели. Учебное пособие для ВУЗов.– М.: НИТИ - 2002, 391 стр.

80. Федосеев В.В. Экономико-математические методы и модели в маркетинге: Учебное пособие / ВЗФЭН / - М.: АО "Финстартинформ", 1996. - 110 с.

81. Филиппов Л.А. Оценка бизнеса и смежные вопросы. Учебное пособие. Барнаул: Изд-во Алт. Университета, 2001. - 470 с.

82. Хазанова Л.Э. Математическое моделирование в экономике. Учебное пособие. - М.: Издательство БЕК, 1998. - 141 с.

83. Хедли Дж. Нелинейное и динамическое программирование. - М.: Мир, 1967.

84. Четыркин Е.М. Статистические методы прогнозирования. - М.: Статистика, 1977.

85. Шелобаев с.И. Математические методы и модели: Учеб. пособие. -М.: ЮНИТИ, 2000. - 366 с. (1474968-ООЛ)

86. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. Учебное пособие. - М.Ж Дело, 200. - 440 с.

87. Шухов Н.С., Фрейдлин М.П. Математическая экономия в России (1865-1995 гг.). М.: Наука, 1996. - 351 с.

88. Эддоус М., Стенсфилд Р. Методы принятия решений/ Пер. с англ. Под ред. И. И. Елисеевой. - М.: Аудит, Юнити, 1997. - 590 с.

89. Экономико-математические методы и модели: Метод. указ. / Сост. с.В. Местников. – Якутск: Изд-во ЯГУ, 2001. - 37 с.

90. Экономико-математические методы и модели: Метод. указ. к выполнению контрольной работы / Сост. с.В. Местников, И.В. Николаева. – Якутск: Изд-во ЯГУ, 2001. - 39 с.

91. Экономико-математические методы и модели: Учеб. пособие / Под общ. ред. А.Л. Кузнецова. – Минск: БГЭУ, 2000. - 411 с.

92. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов/ В.В.Федосеев, А.Н.Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В.Федосеева -М.: ЮНИТИ, 1999. -391с.