 |
Главная |
Аффинная система координат.
|
из
5.00
|
ГОУВПО «Арзамасский государственный педагогический институт
имени А.П.Гайдара»
Кафедра алгебры, геометрии и методик их преподавания.
Дипломная работа
«Многомерные пространства»
Выполнил: студент 54 группы
физико-математического факультета
Карасёв Алексей
Научный руководитель кандидат
физико-математических наук,
доцент: Елисеев Е.М .
Арзамас 2008г.
Введение.
Глава 1. Аффинное пространство.
Аффинное n -мерное пространство.
Аффинная система координат.
Квадрики в аффинном пространстве.
Классификация квадрик в аффинном пространстве.
Различные виды уравнений k -плоскостей.
Взаимное расположение k -плоскостей.
Расстояние между k -плоскостями.
Глава 2. Евклидово пространство.
N- мерное евклидово пространство.
Расстояние между двумя точками. Угол между векторами.
Движения евклидова пространства.
1.4. Группы движений пространства 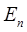 .
.
Преобразование подобия. Группа подобий.
Квадрики в евклидовом n -пространстве.
Задачи.
Заключение.
Литература.
Введение.
Многомерная геометрия- геометрия пространств размерности, большей трёх. Термин «Многомерная геометрия» применяется к тем пространствам, геометрия которых была первоначально развита для случая трёх измерений и только потом обобщена на число измерений n>3, то есть прежде всего к евклидову пространству, а также к пространству Лобачевского, Римана, проективному, аффинному.
Исторически представление в более чем 3-мерном пространстве зарождалось постепенно; первоначально - на почве геометрического представления степеней:  - «квадрат»,
- «квадрат»,  - «куб», но
- «куб», но  и т.д. уже не имеет наглядного представления, и говорили
и т.д. уже не имеет наглядного представления, и говорили  - «биквадрат»,
- «биквадрат»,  - «кубоквадрат» и т.п. (еще у Диофанта в 3в. и далее ряда средневековых авторов). Мысль о многомерном пространстве выражал И.Кант (1746 г), а о присоединении к пространству в качестве 4-й координаты времени писал Ж. Д´ Аламбер. Построение же евклидовой многомерной геометрии было осуществлено А.Кэли (1843г.), Г.Грассманом (1844г.) и Л.Шлефли(1852г.). Первоначальные сомнения и мистика, связанные со смешением этих обобщений с физическим пространством, были преодолены, и n-мерное пространство как плодотворно формально-математическое понятие скоро полностью укрепилось в математике.
- «кубоквадрат» и т.п. (еще у Диофанта в 3в. и далее ряда средневековых авторов). Мысль о многомерном пространстве выражал И.Кант (1746 г), а о присоединении к пространству в качестве 4-й координаты времени писал Ж. Д´ Аламбер. Построение же евклидовой многомерной геометрии было осуществлено А.Кэли (1843г.), Г.Грассманом (1844г.) и Л.Шлефли(1852г.). Первоначальные сомнения и мистика, связанные со смешением этих обобщений с физическим пространством, были преодолены, и n-мерное пространство как плодотворно формально-математическое понятие скоро полностью укрепилось в математике.
Евклидово пространство произвольного числа измерений n  (не исключая случая бесконечно - мерного) проще всего определить как такое , в котором выделены подмножества – прямые и плоскости, имеются обычные отношения : принадлежности порядка, конгруэнтности (либо определены расстояния или движения), и выполняются все обычные аксиомы, кроме следующей: две плоскости , имеющие общую точку, имеют по крайней мере еще одну. Если это выполнено, то пространство 3-мерно, если же не выполнено, так что есть две плоскости с единственной общей точкой, то пространство, как минимум , 4- мерно.
(не исключая случая бесконечно - мерного) проще всего определить как такое , в котором выделены подмножества – прямые и плоскости, имеются обычные отношения : принадлежности порядка, конгруэнтности (либо определены расстояния или движения), и выполняются все обычные аксиомы, кроме следующей: две плоскости , имеющие общую точку, имеют по крайней мере еще одну. Если это выполнено, то пространство 3-мерно, если же не выполнено, так что есть две плоскости с единственной общей точкой, то пространство, как минимум , 4- мерно.
Совершенно аналогично евклидову пространству  определяются пространство Лобачевского
определяются пространство Лобачевского  и аффинное
и аффинное  . В пространстве
. В пространстве  выполняются все те же аксиомы, что в
выполняются все те же аксиомы, что в  , с заменой аксиомы параллельности на противоположную, а в
, с заменой аксиомы параллельности на противоположную, а в  - все аксиомы
- все аксиомы  за исключением аксиом конгруэнтности, вместе с которыми исключается и само понятие конгруэнтности. Аналогично, изменением аксиом сочетания можно определить n-мерное проективное пространство
за исключением аксиом конгруэнтности, вместе с которыми исключается и само понятие конгруэнтности. Аналогично, изменением аксиом сочетания можно определить n-мерное проективное пространство  . Другой способ определения всех этих пространств состоит в том, что в них вводятся координаты, задается группа их преобразований и геометрическими считаются те и только те соотношения, которые инвариантны относительно этой группы. В случае
. Другой способ определения всех этих пространств состоит в том, что в них вводятся координаты, задается группа их преобразований и геометрическими считаются те и только те соотношения, которые инвариантны относительно этой группы. В случае  – это группа подобий; для
– это группа подобий; для  - это группа всех линейных (неоднородных) преобразований.
- это группа всех линейных (неоднородных) преобразований.
Аффинное n -мерное пространство.
Пусть V-векторное пространство над полем K .Элементы из V будем обозначать так:  ,
,  ,…,
,…,  ,
, 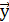 ,…. Множество E
,…. Множество E  называют аффинным пространством над векторным пространством V над полем K,если задано отображение
называют аффинным пространством над векторным пространством V над полем K,если задано отображение  : E
: E  E
E  V, удовлетворяющая двум условиям (аксиомам Вейля аффинного пространства):
V, удовлетворяющая двум условиям (аксиомам Вейля аффинного пространства):
1. Для каждого элемента A  E отображение
E отображение  : E
: E  V по закону
V по закону  ( B )=
( B )=  ( A , B ),
( A , B ),  B
B  является биекцией.
является биекцией.
Каждой упорядоченной паре (A , B ) элементов A , B  E отображение
E отображение  ставит в соответствие определенный вектор
ставит в соответствие определенный вектор  (A , B )=
(A , B )=  V . Этот вектор обозначают через
V . Этот вектор обозначают через  . По аксиоме 1 для каждых A
. По аксиоме 1 для каждых A  E ,
E ,  V существует и притом единственный элемент X
V существует и притом единственный элемент X  , такой, что
, такой, что  =
= 
2.  +
+  =
=  ,
, 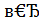 A , B , C
A , B , C  E .
E .
Элементы A , B , C ,...аффинного пространства E называются точками. Векторы  ,…из V называются переносами (или свободными векторами) пространства E , а векторное пространство V -пространством переносов аффинного пространства E .
,…из V называются переносами (или свободными векторами) пространства E , а векторное пространство V -пространством переносов аффинного пространства E .
Отметим некоторые следствия из определения аффинного пространства:
1)  =
=  =
=  По аксиоме 2
По аксиоме 2
 +
+  =
=  (1)
(1)
 +
+  =
=  (2)
(2)
(1), (2) 
 +
+  =
=  +
+ 
Вычитая из обеих частей равенства вектор  =
=  , получим
, получим
 =
=  ;
;
2) вектор  - нулевой вектор пространства переносов. Для любых A , B
- нулевой вектор пространства переносов. Для любых A , B  имеем:
имеем: 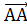 +
+  =
=  =
=  , где
, где  - нулевой вектор пространства V . Так как в векторном пространстве V нулевой вектор единственный, то
- нулевой вектор пространства V . Так как в векторном пространстве V нулевой вектор единственный, то  =
= 
 A , B
A , B  E ;
E ;
3)  =-
=-  По аксиоме 2
По аксиоме 2  +
+  =
=  +
+  =
=  т.е. векторы
т.е. векторы  и
и  пространства V противоположны один другому и, значит,
пространства V противоположны один другому и, значит,  =-
=- 
4)  =
=  A = B . По аксиоме 2
A = B . По аксиоме 2  +
+  =
=  и так как по условию
и так как по условию  =
=  то
то  =
=  . Значит, -
. Значит, -  = -
= -  и по следствию 3
и по следствию 3  =
=  . Отсюда по аксиоме 1 A = B .
. Отсюда по аксиоме 1 A = B .
Аффинная система координат.
Пусть Е n -мерное аффинное пространство над полем К, V –пространство переносов. Аффинной системой координат, или аффинным репером в пространстве Е, называется упорядоченное множество R из n +1 точек О,  ,
,  …,
…,  таких, что векторы
таких, что векторы  =
=  (
(  =1,2,…,n) образуют базис пространства V. Точки
=1,2,…,n) образуют базис пространства V. Точки 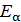 будут определены , если задать точку О
будут определены , если задать точку О  и базис {
и базис {  } в V . Поэтому вместо R ={ O ,
} в V . Поэтому вместо R ={ O ,  …,
…,  } обычно пишут: R =
} обычно пишут: R =  …,
…,  }.Точку O называют началом репера R , векторы
}.Точку O называют началом репера R , векторы  -координатными векторами.
-координатными векторами.
Зададим в аффинном пространстве Е какой-либо репер R ={ O ,  ,
,  ,…
,… 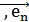 }.Для каждой точки M
}.Для каждой точки M  E определен вектор
E определен вектор  , который называется радиус – вектор точки M . Вектор
, который называется радиус – вектор точки M . Вектор 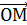 разложим по векторам базиса {
разложим по векторам базиса { 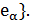
 =
= 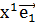 +
+  +…+
+…+  , (3)
, (3)
где  ,
,  ,…,
,…,  - элементы поля К; они называются координатами точки M в репере R.
- элементы поля К; они называются координатами точки M в репере R.
Формулу (3) можно записать короче:
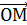 =
=  , или
, или 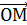 =
=  . (4)
. (4)
Индекс у буквы x показывает номер координаты.
Кроме выбранного репера R , в аффинном пространстве существуют и другие аффинные реперы. Возьмем еще один репер R ´={ O ´,  …,
…,  }. Пусть
}. Пусть 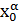 - координаты точки O ´ в репере R :
- координаты точки O ´ в репере R :
 ´=
´=  . (5)
. (5)
Вектор  ´=
´=  (
(  разложен по векторам старого базиса {
разложен по векторам старого базиса {  }, причем определитель det
}, причем определитель det  матрицы C=
матрицы C=  отличен от нуля ,так как векторы
отличен от нуля ,так как векторы  ´,
´,  …,
…,  образуют базис пространства V.
образуют базис пространства V.
Матрица С называется матрицей перехода от старого базиса {  } к новому базису {
} к новому базису {  ´}.
´}.
Для произвольной точки M  Е имеем:
Е имеем:
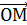 =
=  ´+
´+  . (6)
. (6)
Пусть  – координаты точки М в репере R и
– координаты точки М в репере R и  – координаты этой же точки в репере R ´. Учитывая (5), запишем равенство (6) в виде:
– координаты этой же точки в репере R ´. Учитывая (5), запишем равенство (6) в виде:  =
=  +
+  .
.
Используя (  , получим:
, получим:
 =
=  +
+  Отсюда в силу линейной независимости векторов
Отсюда в силу линейной независимости векторов  :
:
 =
=  , det
, det  (7)
(7)
Равенства (7) выражают старые координаты точки М через ее новые координаты и представляют собой формулы преобразования координат точки М  Е.
Е.
Пусть Е- n-мерное аффинное пространство над полем К, V -пространство переносов. Если взять точку О, то по первой аксиоме Вейля отображение  :E
:E  V по закону
V по закону  (М)=
(М)=  является биекцией.
является биекцией.
С помощью этой биекции можно отождествить аффинное пространство E и векторное пространство V (отождествить каждую точку М  Е с ее радиус-вектором
Е с ее радиус-вектором  V).
V).
Квадрики в аффинном пространстве.
Квадрикой (или поверхностью второго порядка) Q в аффинном пространстве  называется место точек этого пространства, координаты которых в каком–либо аффинном репере R ={ O ,
называется место точек этого пространства, координаты которых в каком–либо аффинном репере R ={ O ,  } удовлетворяют алгебраическому уравнению второй степени:
} удовлетворяют алгебраическому уравнению второй степени:
 +2
+2  +
+  =0. (1)
=0. (1)
Перенесем начало координат в точку 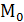 (
(  , т.е. перейдем к реперу R ´={
, т.е. перейдем к реперу R ´={ 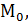
 }. Формулы преобразования координат при этом имеют вид:
}. Формулы преобразования координат при этом имеют вид:
 =
=  +
+ 
где  -старые, а
-старые, а  - новые координаты точки M .
- новые координаты точки M .
Уравнение квадрики в новых координатах примет вид: 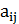 (
(  +
+  )(
)(  +
+  )+2
)+2  (
(  +
+  )+
)+  =0 или
=0 или
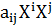 +2
+2  +
+  =0, (2) где
=0, (2) где  =
= 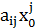 +
+ 
 =
= 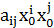 +2
+2  +
+  (3)
(3)
Центром квадрики Q называется ее центр симметрии.
Если в уравнении (2)  =0 (i =1,2,…, n ) и М(
=0 (i =1,2,…, n ) и М( 
 то и М´(-
то и М´(-  )
)  Q и ,значит,
Q и ,значит, 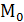 - центр квадрики Q .
- центр квадрики Q .
Верно и обратно: если 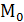 - центр квадрики Q, то в уравнении(2) не будет членов с первыми степенями
- центр квадрики Q, то в уравнении(2) не будет членов с первыми степенями  :
:  =0.
=0.
Пусть 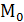 - центр квадрики Q и M (
- центр квадрики Q и M ( 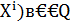 и, следовательно, координаты
и, следовательно, координаты  точки M удовлетворяют уравнению (2). Тогда и M´(-
точки M удовлетворяют уравнению (2). Тогда и M´(-  )
)  :
: 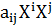 -2
-2  +
+  =0 . (4)
=0 . (4)
Вычитая равенство (4) из равенства (2), находим
 =0 . (5)
=0 . (5)
Этому уравнению удовлетворяют координаты любой точки M  .
.
Теорема. Точка 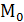 является центром квадрики (1) тогда и только тогда, когда координаты этой точки удовлетворяют системе уравнений:
является центром квадрики (1) тогда и только тогда, когда координаты этой точки удовлетворяют системе уравнений:  +
+  =0. (6)
=0. (6)
При решении системы (6) встречаются три случая.
1. det 
 0,т.е. ранг
0,т.е. ранг  =n. Система (6) имеет единственное решение, и, значит, квадрика Q –единственный центр. Такая квадрика называется центральной.
=n. Система (6) имеет единственное решение, и, значит, квадрика Q –единственный центр. Такая квадрика называется центральной.
2. det  =0,но ранг
=0,но ранг  = ранг
= ранг  =r. Система (6) совместна,
=r. Система (6) совместна,
и в ней можно оставить лишь r  n линейно независимых уравнений. Они определяют (n - r)-плоскость (плоскость центров), каждая точка которой служит центром квадрики.
n линейно независимых уравнений. Они определяют (n - r)-плоскость (плоскость центров), каждая точка которой служит центром квадрики.
3.det  =0,но ранг
=0,но ранг  ранг
ранг  . Система (6) несовместна,- квадрикаQ не имеет центра.
. Система (6) несовместна,- квадрикаQ не имеет центра.
В случае 2 и 3 квадрика называется нецентральной.
Классификация квадрик в аффинном пространстве.
Пусть относительно репера R ={ O ,  квадрика Q определяется уравнением:
квадрика Q определяется уравнением:
 +2
+2  +
+  =0 (1)
=0 (1)
Переход к другой аффинной системе координат (к другому реперу R ´={ O ´,  ) можно выполнить в два приема:
) можно выполнить в два приема:
а) перенос начала: от репера R переходим к реперу  ={O´,
={O´,  с теми же координатными векторами
с теми же координатными векторами  . При этом коэффициенты
. При этом коэффициенты 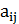 квадратичной формы
квадратичной формы  не изменяются ,тогда как коэффициенты
не изменяются ,тогда как коэффициенты  и свободный член
и свободный член  вообще изменяются;
вообще изменяются;
б) замена базиса {  на базис {
на базис {  } в пространстве переносов V:
} в пространстве переносов V:  =
= 
При этом старые координаты  любой точки M выражаются через ее новые координаты
любой точки M выражаются через ее новые координаты  с помощью системы уравнений :
с помощью системы уравнений :  =
=  Внесем эти выражения
Внесем эти выражения  в уравнение (1), получим уравнение квадрики Q в новых координатах
в уравнение (1), получим уравнение квадрики Q в новых координатах  :
:
 +2
+2  +
+  =0, (2)
=0, (2)
Следовательно, при замене базиса {  изменяются коэффициенты квадратичной формы
изменяются коэффициенты квадратичной формы  и коэффициенты
и коэффициенты  но не меняется свободный член
но не меняется свободный член  . При любом преобразовании аффинной системы координат ранг и индекс квадратичной формы
. При любом преобразовании аффинной системы координат ранг и индекс квадратичной формы  не меняются.
не меняются.
Уравнение квадрики, имеющей хотя бы один центр имеет вид:  (
(  +
+  +…+
+…+  +
+  =0 . (
=0 . ( 
Уравнение квадрики, не имеющей центра  (
(  +…+
+…+  (
(  +2b
+2b 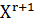 =0 . (
=0 . (  )
)
Рассмотрим уравнение (  . Возможны следующие частные случаи:
. Возможны следующие частные случаи:
1. r = n. Уравнение определяет центральную квадрику (с центром в точке  =0).
=0).
А)  - центр не лежит на квадрике. Пусть
- центр не лежит на квадрике. Пусть 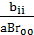 =-
=-  , приведем уравнение (
, приведем уравнение ( 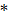 ) к каноническому виду:
) к каноническому виду:
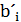 (
(  =1 (3)
=1 (3)
 Если в уравнении (3) все коэффициенты положительны,
Если в уравнении (3) все коэффициенты положительны, 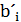
 , то, обозначив
, то, обозначив  =
= 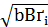
 , получим нормальное уравнение эллипсоида:
, получим нормальное уравнение эллипсоида:
(  + (
+ (  +… +(
+… +(  =1.
=1.
 ) В уравнении (3) все
) В уравнении (3) все  . Обозначив
. Обозначив  =
=  , получим нормальное уравнение мнимого эллипсоида (не содержит ни одной точки из
, получим нормальное уравнение мнимого эллипсоида (не содержит ни одной точки из  ):
):
(  + (
+ (  +… +(
+… +(  =-1;
=-1;
 ) В уравнении (3):
) В уравнении (3):  (t=1,2,…,n-l) ,
(t=1,2,…,n-l) ,  (s=n-l+1,…n). Такая квадрика называется гиперболоидом индекса l . Полагая
(s=n-l+1,…n). Такая квадрика называется гиперболоидом индекса l . Полагая 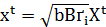 ,
,  , найдем нормальное уравнение этой квадрики:
, найдем нормальное уравнение этой квадрики:  +
+  +…+
+…+  -…-
-…-  =1.
=1.
Б)  =0- центр лежит на квадрике. Ее каноническое уравнение:
=0- центр лежит на квадрике. Ее каноническое уравнение:  =0 (
=0 (  =
= 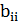 ). (4)
). (4)
Квадрика называется конусом с вершиной в точке О.
 ) Все
) Все  имеют одинаковые знаки. Квадрика называется мнимым конусом (квадрика содержит лишь одну точку О
имеют одинаковые знаки. Квадрика называется мнимым конусом (квадрика содержит лишь одну точку О  ). В этом случае уравнение (4) приводится к виду:
). В этом случае уравнение (4) приводится к виду:
 +…+
+…+  =0.
=0.
 В уравнении (4):
В уравнении (4):  (t=1,2,…,n-l) ,
(t=1,2,…,n-l) ,  (s=n-l+1,…,n). Квадрика Q называется конусом индекса l ,если l
(s=n-l+1,…,n). Квадрика Q называется конусом индекса l ,если l 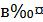 n-l,т.е. l
n-l,т.е. l  .
.
2. r  n.Система уравнений, определяющих центр:
n.Система уравнений, определяющих центр:  =0 (t=1,2,…,r); учитывая что
=0 (t=1,2,…,r); учитывая что  ). Значит, множество центров – ( n - r )-мерная координатная плоскость
). Значит, множество центров – ( n - r )-мерная координатная плоскость  .
.
А) 
 . Обозначив
. Обозначив  =-
=-  , запишем уравнение (1) в каноническом виде:
, запишем уравнение (1) в каноническом виде:
 =1 (t=1,2,…,r). (5). Квадрика называется цилиндром.
=1 (t=1,2,…,r). (5). Квадрика называется цилиндром.
Все виды квадрик аффинно различны. Это значит, что не существует аффинного преобразования, которое переводило бы квадрику одного вида в квадрику другого вида. Квадрики, не принадлежащие одному виду, имеют различные нормальные уравнения.
Выпишем канонические уравнения квадрик в трехмерном аффинном пространстве.
а) r =3. Тогда:
1)  +
+  +
+  =1 (
=1 (  ) -эллипсоид;
) -эллипсоид;
2)  +
+  +
+  =-1 (
=-1 (  )- мнимый эллипсоид;
)- мнимый эллипсоид;
3)  +
+  -
-  =1 (
=1 (  ) - однополостный гиперболоид (гиперболоид индекса 1);
) - однополостный гиперболоид (гиперболоид индекса 1);
4)  -
-  -
-  =1 (
=1 (  ) - двуполостный гиперболоид;
) - двуполостный гиперболоид;
5)  +
+  +
+  =0 (
=0 (  )- мнимый конус;
)- мнимый конус;
6)  +
+  -
-  =0 (
=0 ( 
 ) - конус с вершиной в точке O.
) - конус с вершиной в точке O.
б). r  . Тогда:
. Тогда:
7)  +
+


